Содержание

1. Ортогональное планирование первого порядка 3

1.1 Определяем вид математической модели процесса 3

1.2 Составление матрицы плана, определение числа

точек плана,кодирование факторов 3

1.3 Эксперимент по определению значений функции отклика 4

1.4 Определяем среднее значение функции отклика при каждом

сочетании факторов 4

1.5 Вычисляем значение дисперсии результатов опытов в каждой

строке 5

6. Проверяем однородность дисперсии эксперимента 6

7. Вычисляем коэффициент уравнения регрессии 9

1.8 Статистическая оценка значимости коэффициентов регрессии 9

1.9 Проверка математической модели на адекватность 11

2. Поиск области экстремума 14

3 Ортогональное планирование второго порядка 16

3.1 Составляем матрицу плана 17

3.2 Вычисляем произведение среднего значения функции отклика в

строке на соответствующие значения факторов 19

3.3 Вычисление значений сумм в столбцах 20

3.4 Проверка воспроизводимости эксперимента 22

3.5 Вычисление коэффициентов модели 22

3.6 Статистическая оценка значимости коэффициентов модели 24

3.7 Проверка адекватности модели 25

3.8 Переход от кодированных значений переменных к

фактическим значениям 26

3.9 Построение графика уравнения регрессии 28

3.10 Определение экстремума уравнения регрессии 29

1. Ортогональное планирование первого порядка

Ортогональным планированием называется такое планирование, при котором уровни факторов выбираются симметрично относительно центра плана.

Пусть в лабораторных условиях исследуется процесс потери двигателем компрессии в зависимости от двух факторов: износа колец ε и потери упругости кольцами η. Требуется составить матрицу планирования и получить математическую модель явления.

1.1 Определяем вид математической модели процесса

На первом этапе исследования явление описывается с помощью линейной модели вида

(1.1)

где х₁ и х₂ – факторы, определяющие поведение модели;

В₀, В₁ и В₂ – коэффициенты линейной модели.

1.2 Составление матрицы плана, определение числа точек плана,кодирование факторов

Составляем матрицу планирования, которая имеет число точек N

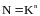(1.2)

где К – число уровней варьирования факторов ε и η;

n – число факторов.

На этом этапе каждый фактор принимает значения на двух уровнях:

х_1min, x_1max, x_2min, x_2max, т.е. К = 2.

Для дальнейших вычислений факторы кодируем. Минимальное значение фактора кодируется значением –1, максимальное значение кодируется значением +1. Кроме того, вводится дополнительный фактор х₀, во всех случаях имеющий значение х₀ = +1.

Число точек матрицы планирования

Пусть факторы имеют минимальные значения

ε_min = 6, η_min= 3,

и максимальные значения

ε_mах = 12, η_maх = 9.

Кодирование факторов заключается в замене фактических значений факторов фиктивными значениями, позволяющими существенно упростить дальнейшие вычисления.

Верхнее значение х_1в фактора ε определяем по зависимости

(1.3)

где Δε – шаг изменения фактора ε.

При ортогональном планировании первого порядка шаг варьирования фактора равен разности Δε = ε_mах – ε_min. Поэтому х_1в = +1.

Аналогично

(1.4)

(1.5)

(1.6)

Матрица плана будет иметь вид, показанный в таблице 1.1, и ее записываем в табличном редакторе ЕXEL.

Таблица 1.1 Матрица планирования эксперимента

Номер опыта (вариант сочетания факторов)	Уровни факторов
	В натуральных значениях		В кодированных значениях
	ε	η	х0	х1	х2
1	75	84	1	– 1	– 1
2	75	144	1	– 1	1
3	105	84	1	1	– 1
4	105	144	1	1	1

1.3 Проводим эксперимент по определению значений функции отклика

Таблица приобретет вид

Номер опыта (вариант сочетания факторов)	Уровни факторов					Результаты опытов (значения функции отклика)
	В натуральных значениях		В кодированных значениях
	ε	η	х0	х1	х2	y1	y2	y3
1	75	84	1	– 1	– 1	92,5	89,5	90,9
2	75	144	1	– 1	1	114,8	117,1	112,3
3	105	84	1	1	– 1	91,7	92,7	93,6
4	105	84	1	1	1	94,2	91	92,7

1.4 Определяем среднее значение функции отклика при каждом сочетании факторов

Средние значения опыта для каждого сочетания факторов определяем с помощью функции СРЗНАЧ в EXEL.

Таблица 1.2 Матрица плана со средними значениями функции отклика для каждого варианта сочетания факторов

Номер опыта (вариант сочетания факторов)	Уровни факторов							Результаты опытов (значения функции отклика)							Сре-днее зна-чение уср
	В натуральных значениях			В кодированных значениях				y1		y2		y3
	ε	η	х0		х1	х2
1	75	84	1		– 1	– 1	92,5		89,5		90,9		90,97
2	75	144	1		– 1	1	114,8		117,1		112,3		114,73
3	105	84	1		1	– 1	91,7		92,7		93,6		92,7
4	105	114	1		1	1	94,2		91		92,7		92,63

1.5 Вычисляем значение дисперсии результатов опытов в каждой строке.

Эта операция производится в EXEL с помощью команды ДИСП. Результаты заносим в следующий столбец таблицы, которая приобретет вид, показанный в таблице 1.3.

Таблица 1.3 Матрица, дополненная значениями дисперсий в каждой строке плана

Номер опыта (вариант сочетания факторов)	Уровни факторов					Результаты опытов (значения функции отклика)			Сред-нее значе-ние уср	Дис-пер-сия D
	В натуральных значениях		В кодированных значениях			y1	y2	y3
	ε	η	х0	х1	х2
1	75	84	1	– 1	– 1	92,5	89,5	90,9	90,97	2,253
2	75	144	1	– 1	1	114,8	117,1	112,3	114,73	5,763
3	105	84	1	1	– 1	91,7	92,7	93,6	92,7	0,903
4	105	144	1	1	1	94,2	91	92,7	92,63	2,563