
- •Неопределённый интеграл
- •Интегрирование методом замены переменных
- •Интегрирование заменой переменных.
- •Интегрирование по частям
- •Интегрирование по частям.
- •Интегрирование функций, содержащих квадратный трёхчлен
- •Интегрирование функций, содержащих квадратный трёхчлен.
- •Интегрирование рациональных дробей
- •Интегрирование рациональных функций
- •Интегрирование тригонометрических функций
- •Интегрирование тригонометрических функций.
- •Интегрирование некоторых иррациональных функций
- •Интегрирование иррациональных функций.
- •Определённый интеграл
- •Основные свойства определённого интеграла
- •Вычисление определённого интеграла
- •Вычисление площади плоской фигуры
- •Вычисление площади
- •Вычисление длины дуги кривой
- •Вычисление длин дуг кривых
- •Вычисление объёма тела вращения
- •Объём тела вращения
- •Задачи физического содержания на применение определённого интеграла
- •Несобственные интегралы
- •Несобственные интегралы от функций, имеющих бесконечный разрыв
- •Несобственные интегралы с бесконечными пределами
Вычисление длины дуги кривой
Длина дуг в прямоугольных координатах. Если кривая y = f(x) на отрезке является гладкой, то длина дуги этой кривой, заключенной между точками с абсциссами x = a, x = b находится по формуле:
![]()
Если кривая задана параметрически
то длина дуги кривой соответствующая монотонному изменению параметра t от до , вычисляется по формуле:

Если гладкая кривая
задана уравнением в полярных координатах
,
то длина дуги кривой, соответствующая
монотонному изменению полярного угла
от
![]() до
до
![]() находится по формуле:
находится по формуле:
![]()
Пример.
Найти длину астроиды
![]()

![]() Так как астроида
симметрична относительно
Так как астроида
симметрична относительно
![]() координатных
осей, то
координатных
осей, то
![]()
Рис.2.
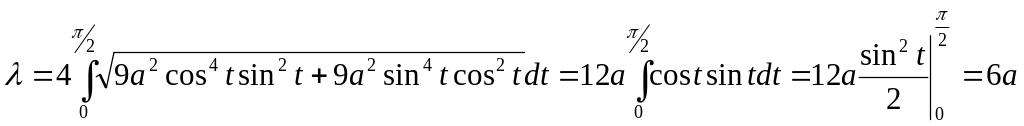
Вычисление длин дуг кривых
Вычислить длину дуги полукубической параболы
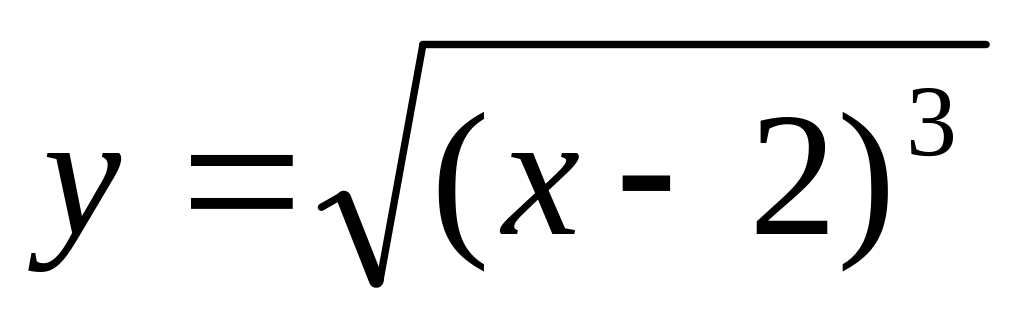 от
точки А(2;0) до точки В(6;8).
от
точки А(2;0) до точки В(6;8).Вычислить длину кардиоиды
 .
.Вычислить длину одной арки циклоиды
 .
.Вычислить длину дуги параболы
 от точки А(0;3) до точки В(4;-1).
от точки А(0;3) до точки В(4;-1).Вычислить длину дуги полуокружности
 от точки А(-1;
от точки А(-1; )
до точки В(1;
).
)
до точки В(1;
).Вычислить длину дуги параболы
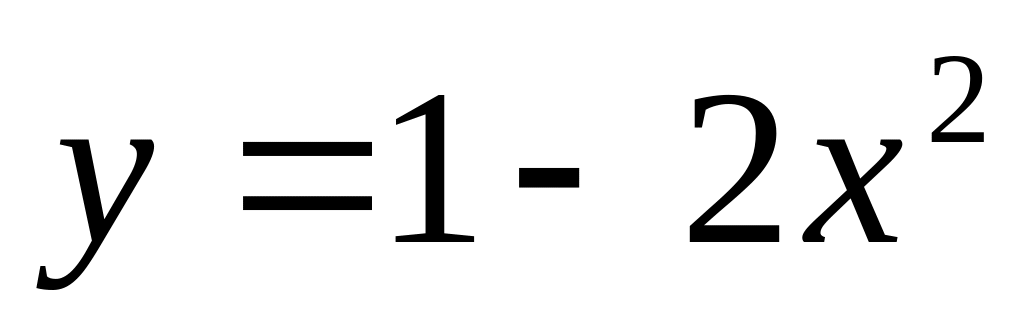 от точки А(0;1) до точки В(1;-1).
от точки А(0;1) до точки В(1;-1).Вычислить длину дуги параболы
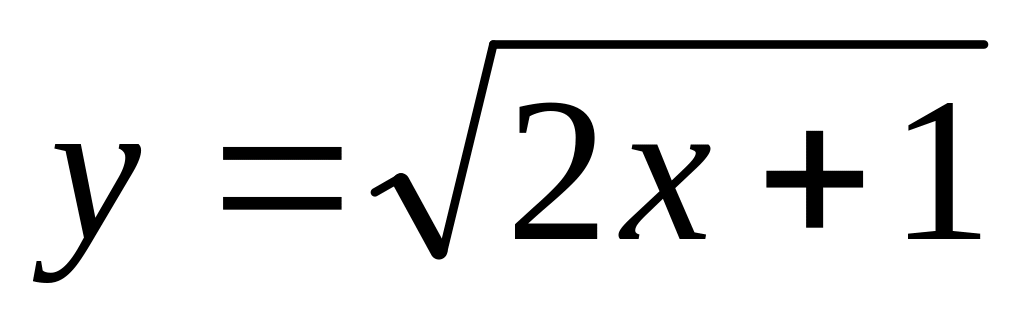 от точки А(0;1) до точки В(4;3).
от точки А(0;1) до точки В(4;3).Вычислить длину дуги кривой
 ,
отсечённой осью Ох.
,
отсечённой осью Ох.Вычислить длину дуги кривой
 между соседними точками пересечения
с осью Ох.
между соседними точками пересечения
с осью Ох.Вычислить длину дуги кривой
 между точками пересечения с осью Ох.
между точками пересечения с осью Ох.Найти длину логарифмической спирали
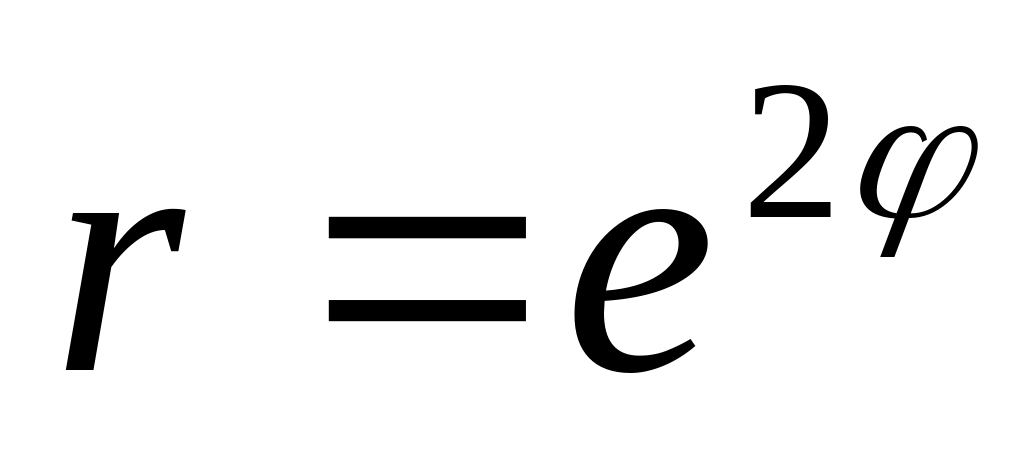 от начала до точки (
от начала до точки ( ).
).Найти длину первого витка архимедовой спирали
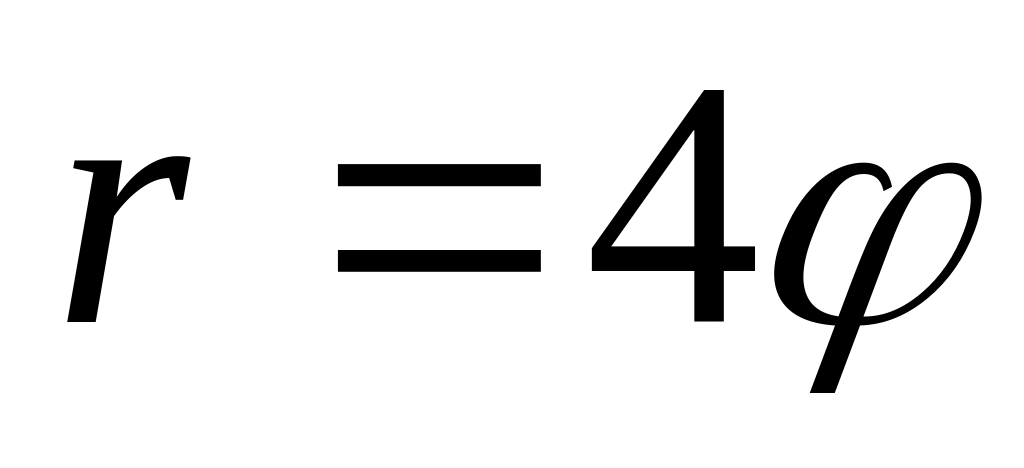 .
.Найти длину всей астроиды
 .
.Вычислить длину петли кривой
 .
.Найти длину кривой
 .
.Вычислить длину дуги развёртки окружности
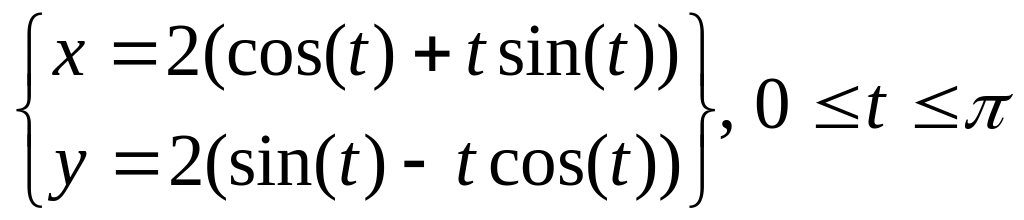 .
.Вычислить длину дуги кривой
 от
от
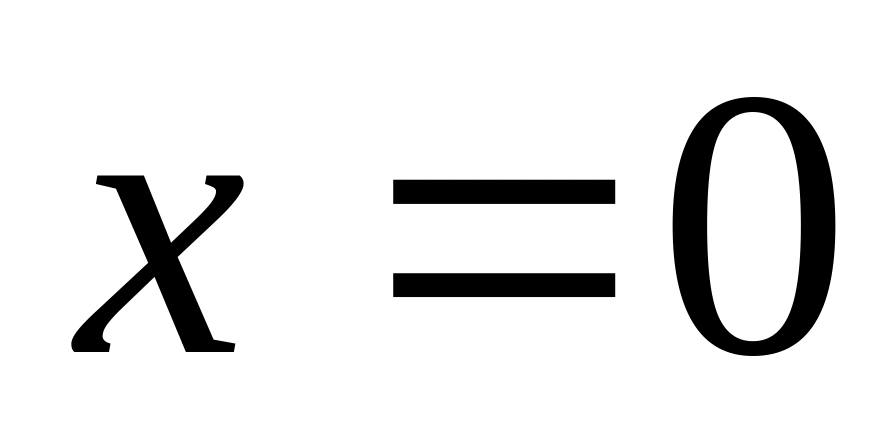 до
.
до
.Вычислить длину дуги кривой
 содержащейся
между
содержащейся
между
 и
и
 .
.Вычислить длину дуги кривой
 содержащейся
между точками (0;1) и (1;е).
содержащейся
между точками (0;1) и (1;е).Вычислить длину дуги кривой
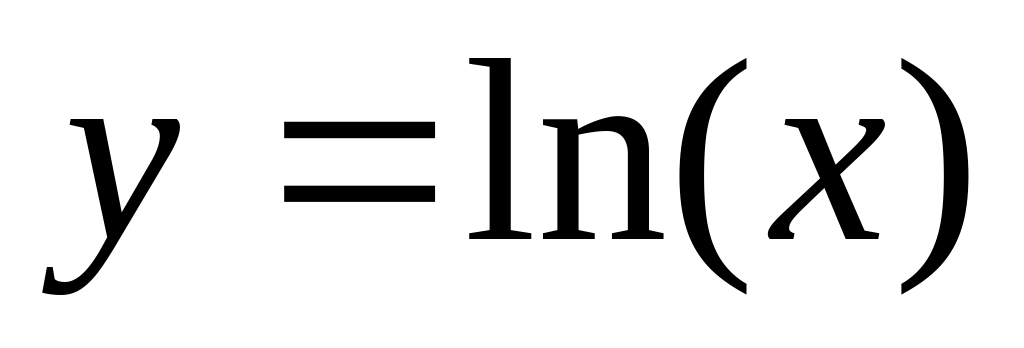 от
от
 до
до
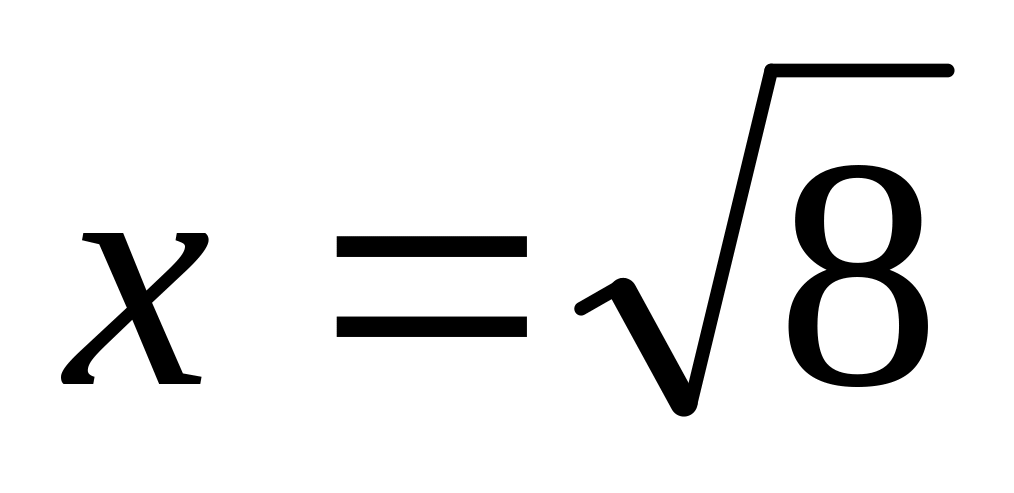 .
.Вычислить длину дуги кривой
 ,
,
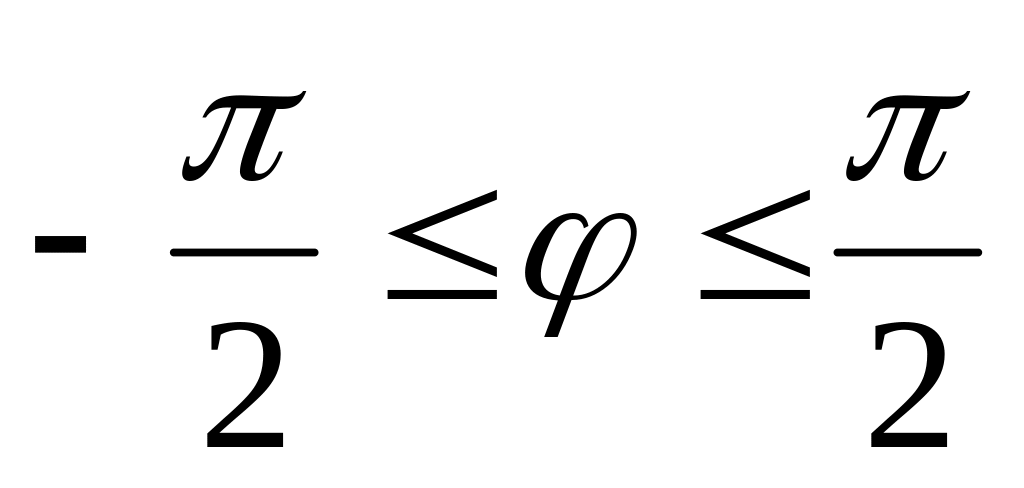 .
.Вычислить длину дуги кривой
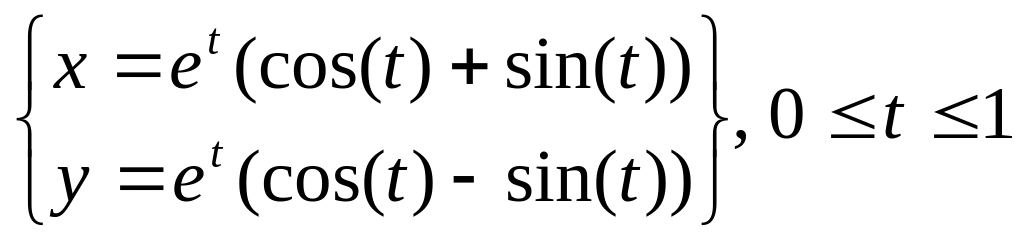 .
.Вычислить длину дуги кривой
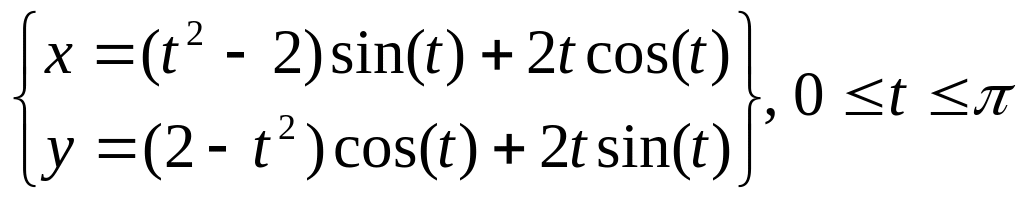 .
.Вычислить длину кривой
 .
.Вычислить длину дуги кривой
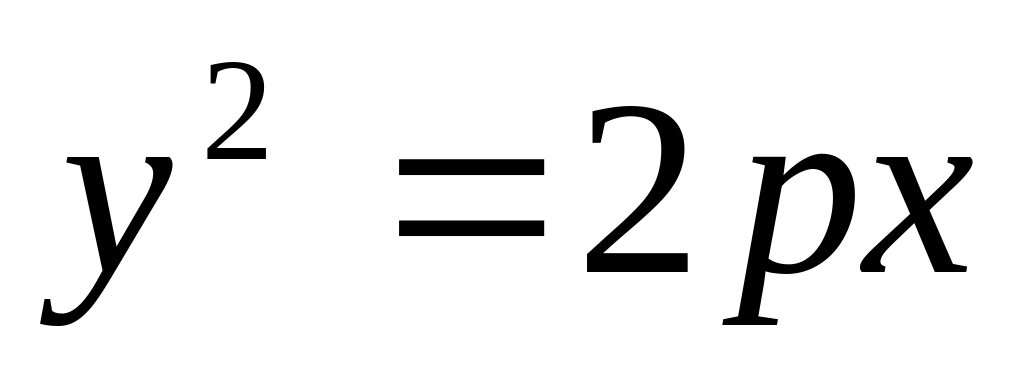 ,
отсечённой прямой
,
отсечённой прямой
 .
.Вычислить длину первого завитка спирали
 .
.Найти длину дуги АОВ кривой
 ,
где А и В имеют одинаковые абсциссы
,
где А и В имеют одинаковые абсциссы
 .
.Вычислить длину дуги кривой
 .
.Вычислить длину дуги кривой
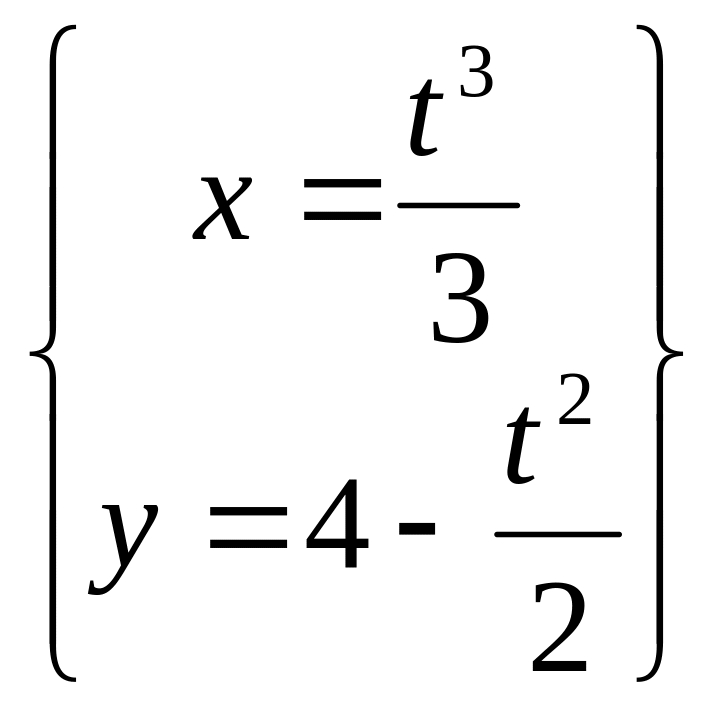 .
.Вычислить длину кривой
 .
.
Вычисление объёма тела вращения
Объём тела, образованного вращением вокруг оси Ох криволинейной трапеции, ограниченной непрерывной кривой у = f(x) и прямыми x = a, x = b, y = 0, находится по формуле:
![]()
Объем тела вращения
вокруг оси Оу криволинейной трапеции,
ограниченной непрерывной кривой
![]() прямыми
прямыми
![]() ,
,
![]() ,
,
находится по формуле:
,
,
находится по формуле:
![]()
Пример: Вычислить объём тора.
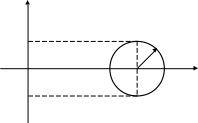 Пусть круг вращается
вокруг
Пусть круг вращается
вокруг
прямой АЕ (рис.3). Тогда объ-
А В ём тора может быть рассмот-
рен как разность объёмов вра-
щения криволинейных трапе-
L C ций ABCDE и ABLDE вокруг
![]() оси Oy.
оси Oy.
E D Уравнение окружности LBCD
Имеет вид:
Рис.3.
![]() , откуда
, откуда
![]() ,
причём уравнение кривой BCD
,
причём уравнение кривой BCD
![]() ,
,
а уравнение кривой BLD
![]() .
.
Следовательно, искомый объём равен:
![]()
