Принцип суперпозиции сил. Равнодействующая сил.

При малых силах справедлив принцип суперпозиции: если с данной частицей взаимодействует несколько других частиц, то результирующая сила, действующая на частицу, равна векторной сумме сил всех парных взаимодействий:

.

Сила называется равнодействующей.

Из принципа суперпозиции сил следует закон независимости движений:

.

Интегральное выражение основного закона динамики

Из основного закона динамики точки следует

- элементарный импульс силы равен изменению импульса частицы.

Для конечного промежутка времени:

, .

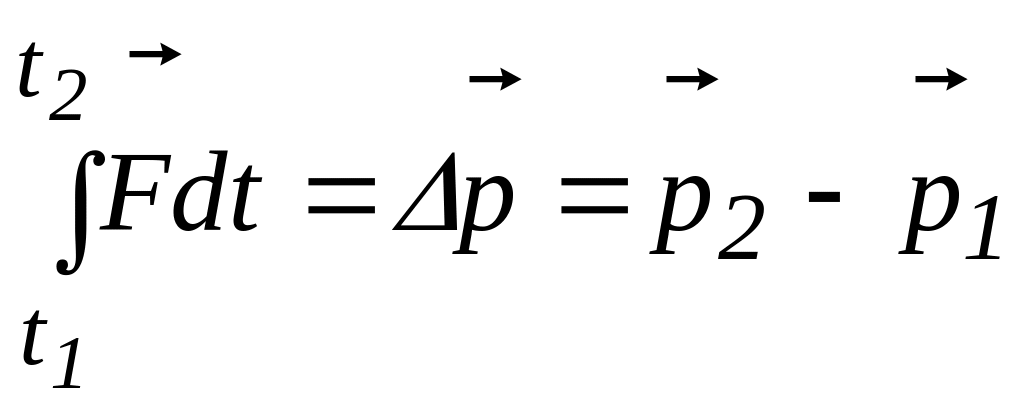Это интегральное выражение основного закона динамики точки, которое может быть представлено как:

,

г де - средняя сила для промежутка времени .

Графическая иллюстрация:

1) ,

,

.

2) ,

,

,

.

3) алгебраическая сумма площадей «+» и «-».

Третий закон Ньютона

Сила действия равна силе противодействия:

или .

Третий закон Ньютона справедлив не всегда.

Динамика систем материальных точек

Рассмотрим систему N взаимодействующих частиц. Силы взаимодействия меду частицами системы называются внутренними (f_ik). Силы взаимодействия частиц системы с частицами, не входящими в систему – внешними (F_i).

Система частиц, не испытывающая внешних взаимодействий, называется замкнутой или изолированной.

Запишем II закон Ньютона для каждой частицы системы:

Согласно III закона Ньютона

Сложим левые и правые части записанных выражений с учётом III закона Ньютона:

.

- суммарный импульс системы частиц.

- сумма внешних сил.

То есть для системы частиц можно записать:

.

Полученное выражение называется законом Ньютона для системы частиц.

Изменение импульса системы определяется внешними силами, т.е. внутренние силы не изменят полного импульса системы.

В случае замкнутой системы имеем , то есть ,

импульс замкнутой системы сохраняется.

Это не означает, что импульс каждой частицы остаётся неизменным. Под действием внутренних сил наблюдается перераспределение импульса между частицами.

Центр инерции системы частиц (тела)

Импульс – величина относительная. Найдём, как преобразуется импульс системы частиц при переходе от одной ИСО (S) к другой ИСО (S’).

В S системе ,

в S’ системе .

Для i – частицы .

Импульс системы частиц

где - масса системы частиц (тела).

Можно подобрать такую систему отсчета S’, в которой . Тогда

.

Отсюда видно, что импульс тела всегда можно представить аналогично импульсу частицы, как произведение массы тела на скорость движения тела (системы частиц):

.

Точку тела, скорость которой совпадает с называют центром инерции тела или центром масс. Найдём координату этой точки. Из выражения для импульса тела:

.

Движение системы частиц (тела) в целом можно связать с движением центра массы

.

Т.к. для замкнутой системы (тела), то - центр инерции свободного тела движется равномерно и прямолинейно. Этот вывод является обобщением закона инерции для системы.

ИСО, связанную с центром инерции системой центра инерции. В этой системе , тело в целом покоится. Чтобы тело вывести из состояния покоя, необходимо приложить внешнюю силу. Внутренние силы не могут вывести тело из состояния покоя.

Если система частиц (тело) испытывает внешнее воздействие, то его импульс изменяется согласно соотношению .

В частном случае ( ): или .

Центр инерции тела движется как материальная точка, в которой сосредоточена вся масса тела.

Полученное соотношение называется основным законом динамики системы частиц.

Интегральное выражение основного закона динамики системы частиц

Изменение импульса системы частиц равно импульсу внешней силы:

,

.

В проекциях на координатные оси:

, , .

Если сумма внешних сил, действующих в каком-либо направлении равна нулю, например, , то или - суммарный импульс частиц для этого направления сохраняется.

Такой случай называется законом сохранения проекции импульса системы частиц.

Лекция 4

Классификация сил

Сила тяготения

З акон всемирного тяготения был открыт Ньютоном и опубликован в 1697г: две материальные точки (частицы) притягиваются друг к другу с силой, пропорциональной их массам, обратно пропорциональной квадрату расстояния между ними и направлена по линии, соединяющей частицы.

, ,

где и - массы частиц, - расстояние между частицами.

В векторной форме .

Знак «-» говорит о том, что сила тяготения направлена против направления вектора .

В законе всемирного тяготения масса выступает как мера тяготения.

Гравитационная постоянная численно равна , при , .

По современным экспериментальным данным .

Сила притяжения между телами зависит от их размеров, конфигурации и распределения массы по объёму. Эту силу можно найти как сумму всех парных притяжений частиц тела.

Расчёты показывают, что для тел, имеющих форму шара сила притяжения ними:

,

где и - массы шаров, - расстояние между центрами шаров.

Притяжение тела к Земле определяется соотношением:

, где ,

где - масса Земли, - масса тела, r – расстояние от тела до центра Земли, - ускорение свободного падения в поле тяжести Земли. У поверхности Земли обозначают .

Эта сила называется силой тяжести.

Сила, с которой тело действует на связи в результате притяжения к Земле, называется весом тела.

Свободно падающее тело не действует на связи и находится в состоянии невесомости. Вес тела может многократно превышать силу тяжести. Такое состояние называется перегрузкой.

Вблизи поверхности Земли можно считать . До высоты 32 км эта величина меняется на 1 %. Такое поле тяжести называется однородным.

Для высот сравнимых с радиусом Земли уменьшением ускорения свободного падения пренебречь нельзя.

Измерение g эквивалентно «взвешиванию» Земли:

.

Строго говоря, масса в законе тяготения (мера тяготения m_T) и масса во втором законе инерции (мера инерции m_И) – это разные коэффициенты. Если , то Землю можно считать неподвижной, при этом центр инерции системы тело + Земля практически совпадает с центром Земли. Тогда силу тяжести, действующую на тело можно записать в следующей форме:

,

где ускорение свободного падения равно

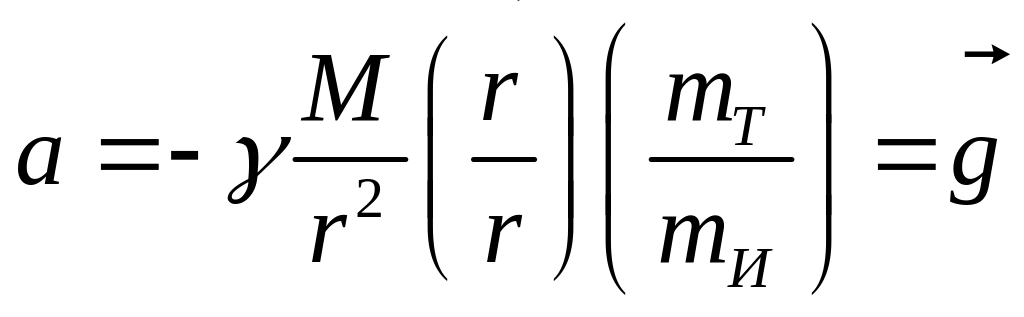при .

Эксперимент показывает, что все тела падают с одним ускорением. Откуда следует, что : масса тяготения равна инертной массе.