Колебательное движение
Это периодически повторяющееся движение точки.
Простейшим и фундаментальным движением является гармоническое колебание.
Для одномерного движения уравнения гармонических колебаний имеет вид:
,
A – амплитуда колебаний,
t – время, (
)
– фаза колебаний,
- начальная фаза,
- циклическая частота (
).
Скорость:
,
Модуль максимальной скорости:
.
Ускорение:
.
Модуль максимального ускорения:
.
Совокупностью гармонических колебаний различных частот и амплитуд можно представить любое движение (гармонический анализ).
Например, равномерное движение по окружности можно получить, суммируя два взаимно перпендикулярных гармонических колебаний одинаковой частоты и амплитуды:
,
- уравнение движения по окружности,
радиуса А.
Скорость:
,
,
,
,
- скорость движения по окружности,
Ускорение:
,
-
нормальное ускорение точки.
Движение твёрдого тела
Твёрдое тело – это физическая абстракция, когда можно пренебречь деформацией тела, т.е. расстояние между любой парой точек тела останется неизменным.
Поступательным называется такое движение твёрдого тела, при котором любая прямая тела остаётся параллельной самой себе и все точки движутся по одинаковым траекториям. Все выводы кинематики материальной точки без изменения можно отнести и к движению центра тяжести твёрдого тела.
При вращении твёрдого тела вокруг неподвижной оси все точки тела движутся по окружности разного радиуса с центром на оси вращения. Общим для всех точек тела будет угол поворота, угловая скорость, угловое ускорение.
Все выводы относительно движения точки по окружности автоматически можно перенести для характеристики вращения твёрдого тела вокруг неподвижной оси.
Любое сложное движение можно свести к комбинации поступательного движения центра масс и вращения тела относительно центра масс.
Лекция 3 Динамика материальной точки Первый закон Ньютона. Преобразования Галилея
Свободная частица – это частица, не взаимодействующая с другими частицами и полями.
Первый закон Ньютона (закон инерции): свободная частица движется равномерно и прямолинейно или покоится.
Системы отсчёта, в которых свободная частица покоится или движется равномерно прямолинейно, называются инерциальными (ИСО).
З
аконы
механики во всех ИСО имеют один и тот
же вид, т.е. не меняются при переходе от
одной ИСО к другой.
Физические величины и соотношения, которые не меняются при переходе из одной ИСО в другую, называются инвариантами (invar).
Пусть имеется ИСО (
),
которая движется относительно неподвижной
ИСО (S) со скоростью
.
Для них справедливы преобразования
Галилея:
,
.
Время во всех ИСО течёт одинаково и в одну сторону (t>0).
В S и S’ инвариантами являются:
интервалы времени
,
расстояния (длины)
.
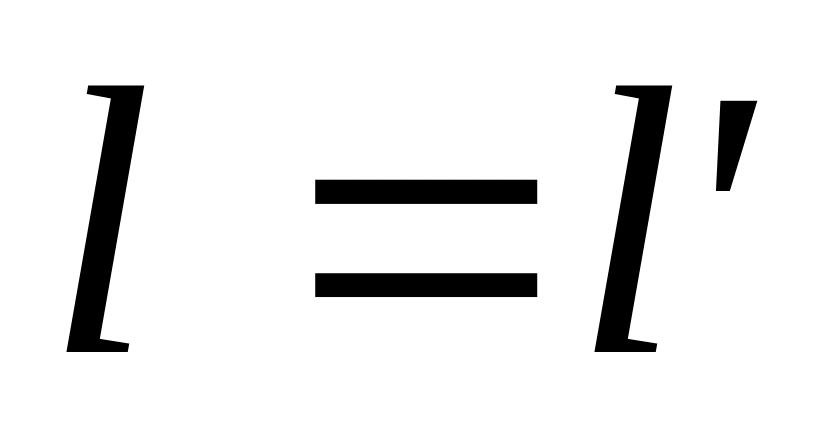Так при
имеем
.
Скорость является относительной величиной и преобразуется согласно закону сложения скоростей:
,
,
=
,
.
Второй закон Ньютона
Импульс (количество движения) – это векторная мера механического движения
,
где
-
масса – это коэффициент пропорциональности,
скаляр, m>0, инвариант.
.
Импульс – величина относительная. Если в S системе , то в системе S’
.
Импульс свободной частицы в ИСО не изменяется:
т.к.
→
.
Сила – мера механического взаимодействия между частицами (телами).
Зависимость силы от влияющих на нее
величин устанавливается экспериментально
и называется законом силы, например,
.
Еcли закон силы задан, то уравнение
называется основным законом динамики частицы или вторым законом Ньютона.
Если m=const, второй закон Ньютона приобретает вид:
или 
.
Здесь масса частицы выступает как мера инертности частицы.
-
средняя сила
,
- мгновенная сила
.
.
По второму закону Ньютона можно по силе определить ускорение , а также
,
.