2.2 Расчет перемычки

2.2.1 Исходные данные

Рассчитать перемычку 3ПБ16-37-п сечением 120220 мм длиной 1550 мм для кладки над проемом шириной 1310 мм. Бетон класса В15, рабочая арматура А400, поперечная арматура В500.

Расчетные характеристики бетона класса В 15 в соответствии с п. 2.1.2 [87]:

 расчетное сопротивление бетона осевому сжатию для предельных состояний первой группы ;

 расчетное сопротивление бетона осевому растяжению для предельных состояний первой группы ;

 расчетное сопротивление бетона осевому сжатию для предельных состояний второй группы ;

 расчетное сопротивление бетона осевому растяжению для предельных состояний второй группы ;

 начальный модуль упругости ;

 коэффициент условий работы бетона (при расчете на действие только постоянных и временных длительных нагрузок).

Расчетные характеристики арматуры класса А400 в соответствии с п. 2.2.2 [87]:

 расчетное сопротивление арматуры осевому сжатию для предельных состояний первой группы ;

 расчетное сопротивление арматуры осевому растяжению для предельных состояний первой группы ;

 расчетное сопротивление арматуры растяжению для предельных состояний второй группы ;

 модуль упругости арматуры .

Расчетные характеристики арматуры класса В500 в соответствии с п. 2.2.2 [87]:

 расчетное сопротивление арматуры осевому сжатию для предельных состояний первой группы ;

 расчетное сопротивление продольной арматуры осевому растяжению для предельных состояний первой группы ;

 расчетное сопротивление поперечной арматуры осевому растяжению для предельных состояний первой группы ;

 расчетное сопротивление арматуры растяжению для предельных состояний второй группы ;

 модуль упругости арматуры: .

Коэффициент надежности по назначению здания .

2.2.2 Сбор нагрузок на перемычку

Перемычка работает как однопролетная, свободнолежащая, равномерно нагруженная балка. Схема расположения перемычки представлена на рисунке 2.6.

Нагрузка от веса перекрытия на 1 м ² горизонтальной поверхности представлена в таблице 2.2.

Рисунок 2.6 – Схема расположения перемычки

Таблица 2.2 – Нагрузка от веса перекрытия на 1 м ² горизонтальной поверхности

Наименование	Нормативная нагрузка , кН/м 2	К-нт надежности по нагрузке	Расчетная нагрузка , кН/м 2
1	2	3	4
А. Постоянная
1. Керамогранит мм,	0,245	1,2	0,294
2. Ц/п раствор ,	0,971	1,3	1,262
3. Оклеечная гидроизоляция ,	0,035	1,2	0,042
4. Ж/б плита многопустотная ,	3,117	1,1	3,429

Продолжение таблицы 2.2
1	2	3	4
Итого:	4,368		5,027
Б. Временная
1. Полезная	1,500	1,2	1,800
Итого:	1,500		1,800
Всего:	5,868		6,827

Нагрузка от веса перекрытия на 1 м.п.:

где – расчетная нагрузка от перекрытия;

– грузовая площадь;

– коэффициент надежности по ответственности (в соответствии со ст. 16 п. 7 [108] );

;

где – продольный шаг;

Нагрузка от веса кирпичной кладки на 1 м.п.:

где – ширина кирпичной кладки;

– высота кирпичной кладки

– удельный вес кирпичной кладки;

Нагрузка от собственного веса перемычки на 1 м.п.:

где – ширина перемычки;

– высота перемычки;

– удельный вес железобетона;

Таким образом, на 1 м длины перемычки действует равномерно распределенная расчетная полная нагрузка:

2.2.3 Определение внутренних усилий в сечениях перемычки от внешней нагрузки

Расчетная схема перемычки представлена на рисунке 2.7.

Расчетная длина перемычки:

где – конструктивная длина перемычки;

– длина проема в свету;

Расчетный изгибающий момент от полной расчетной нагрузки без учета частичного защемления на опорах:

Максимальная поперечная сила на опоре от полной расчетной нагрузки:

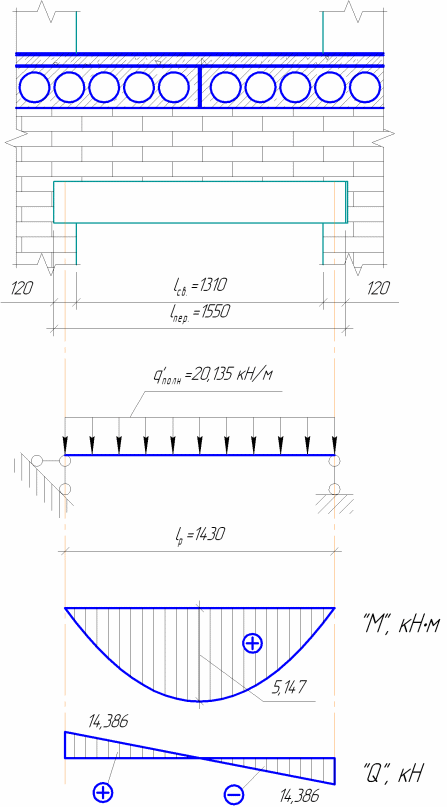
Рисунок 2.7 – Расчетная схема перемычки

2.2.4. Расчет нормальных сечений по прочности

Расчетное сечение перемычки представлено на рисунке 2.8.

Примем толщину защитного слоя , тогда расчетная высота сечения:

Определим значение по формуле:

По таблице 3.2 [61] определим граничную относительную высоту сжатой зоны бетона для арматуры класса А400 , . Так как:

то сжатая арматура по расчету не требуется.

Рисунок 2.8 – Расчетное сечение перемычки

Требуемую площадь сечения растянутой арматуры определим по формуле:

По сортаменту примем арматуру 12А400 с .

2.2.5 Расчет перемычки по полосе между наклонными сечениями

Расчет перемычки по полосе между наклонными сечениями производят из условия:

;

где – поперечная сила в нормальном сечении элемента;

Условие выполняется, прочность бетонной полосы обеспечена.

2.2.6 Расчет перемычки по наклонным сечениям на действие поперечной силы

Проверим обеспечение прочности на действие поперечной силы по наклонной трещине из условия:

где Q – поперечная сила в наклонном сечении с длиной проекции с на продольную ось элемента, определяемая от всех внешних сил, расположенных по одну сторону от рассматриваемого наклонного сечения;

– поперечная сила, воспринимаемая бетоном в наклонном сечении;

– поперечная сила, воспринимаемая поперечной арматурой в наклонном сечении;

где – коэффициент, учитывающий влияние бетона, принимаемый равный 1,5;

– длина проекции наиболее опасного наклонного сечения на продольную ось элемента:

Должны выполняться следующие условия:

Так как:

то прочность бетона не обеспечивает прочность наклонных сечений элемента и поперечная арматура устанавливается по расчету.

Усилие в поперечной арматуре на единицу длины элемента определим по формуле:

Поперечные стержни первоначально примем конструктивно 4В500 с .

Шаг поперечных стержней примем из условия:

Шаг поперечных стержней у опор должен удовлетворять условию:

Примем

Шаг поперечных стержней в пролете должен удовлетворять условию:

Примем

Усилие в поперечной арматуре на единицу длины элемента в приопорном участке:

Условие выполняется, принятой арматуры достаточно.

Определим поперечные усилия, воспринимаемые стержнями поперечной арматуры:

Так как:

то прочность по наклонной трещине обеспечена.

	Лист
	36