19. Статистические методы исследования надежности. Закон Пуассона

Статистические методы используются тогда, когда имеется априорная информация о надёжностных свойствах системы, выраженная статистическими данными испытаний или эксплуатации системы или ее аналогов. В этом случае анализ ведется на основе изучения случайных событий, характеризующих ИС.

Простейший поток случайных событий – пуассоновский. Его параметры не меняются во времени.

Закон Пуассона. Вероятность того, что на интервале времени от 0…t произойдет n случайных событий (отказов) определяется формулой:

– среднее число отказов в период 0…t.

Случайное событие – событие, которое может появиться или не появиться в результате данного опыта.

Время между двумя соседними событиями подчиняется экспоненциальному закону распределения с параметром , т.е. вероятность того, что на участке времени следующего за одним из отказов, не появится ни одного отказа, равна:

Пример:

Определить вероятность того, что за время t =100 ч произойдет 0-2 отказа, если .

Решение:

Среднее число отказов за время t: = 2,5.

Вероятность отсутствия отказов .

Вероятность одного отказа .

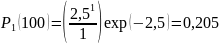Вероятность двух отказов .

20. Статистические методы исследования надёжности. Распределение Вейбулла

Для аппроксимации реальных распределений наработки до отказа на участках приработки, нормальной эксплуатации и старения используют стандартные распределения случайных величин, рассматриваемых в теории вероятности. Для каждого могут рассматриваться следующие характеристики: функция распределения F(t), плотность распределения f(t), математическое ожидание (средняя наработка до отказа) и дисперсия .

Распределение Вейбулла имеет следующие характеристики:

Вероятность безотказной работы ИС за время t:

.

Функция плотности распределения времени (наработки) до отказа:

.

Интенсивность отказов:

.

и – параметры распределения, – параметр формы, – параметр масштаба, – значение времени, при котором плотность вероятности максимальна, в теории вероятностей носит название мода.

При распределение Вейбулла совпадает с экспоненциальным распределением, у которого , при этом – убывающая функция.

Если функции и убывающие.

Если функция – одновершинная, функция непрерывно возрастающая, при – с выпуклостью вверх, а при – с выпуклостью вниз.

При функция является линейной и распределение Вейбулла превращается в распределение Рэлея. При распределение Вейбулла близко к нормальному.

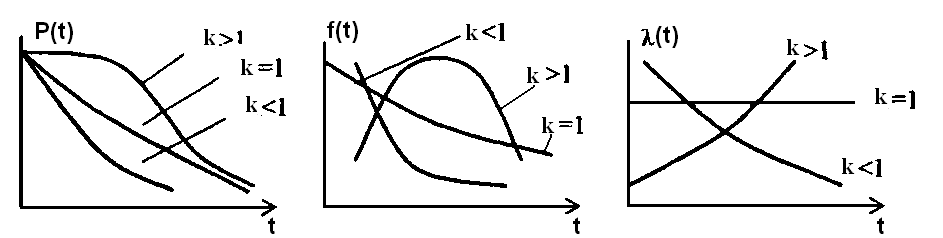
– для электронных устройств с убывающей функцией интенсивности отказов.

– для механических устройств с возрастающей функцией интенсивности отказов.

Экспоненциальное распределение имеет следующие характеристики:

.

Интенсивность отказов постоянна:

.

Экспоненциальное распределение однопараметрическое и обладает одним уникальным свойством: вероятность безотказной работы

.

не зависит от того, сколько времени изделие проработало до рассматриваемого интервала времени . Экспоненциальное распределения является частным случаем распределения Вейбулла (при ).

Пример.

Вероятность безотказной работы ВС за время t = 1000 ч составляет P(1000) = 0,99. Составить прогноз вероятности безотказной работы этой же системы через 100000 часов работы без обслуживания по экспоненциальной модели и модели Вейбулла.

Решение.

В случае выбора экспоненциальной модели получаем

или . Логарифмируя

, откуда

Прогнозируемая вероятность работы через 10⁵ ч.: .

В случае выбора модели Вейбулла примем . Тогда

, откуда .

Прогнозируемая вероятность работы через 10⁵ ч.: .

Прогнозируемые показатели надежности работы объекта зависят от правильно выбранной модели.

Выбор модели надежности – сложная научно-техническая задача. Она решается методами математической статистики. В случаях приближенной оценки выбирается экспоненциальная модель.