8. Типы ошибок в по

1. Ошибки, скрытые в программе:

• Ошибки вычислений.

• Логические ошибки.

• Ошибки ввода-вывода.

• Ошибки манипулирования данными.

• Ошибки совместимости.

Ошибки классифицируются по тяжести последствий и возможности их устранения или парирования:

1. Незначительные ошибки. Эти ошибки проявляются явно или легко обнаруживаются.

2. Средние ошибки (ошибки средней тяжести).

3. Существенные ошибки – ошибки, не устранимые без приостановки функционирования ПС.

9. Надежность по и язык программирования

Количество ошибок в разрабатываем ПО можно существенно снизить за счёт выбора наиболее подходящего языка. Современные высокоуровневые языки, имеющие продуманную структуру, механизмы безопасного управления памятью (сборщик мусора) предупреждают целые классы ошибок, связанные с неправильным управлением памятью, работой с ресурсами и проч.

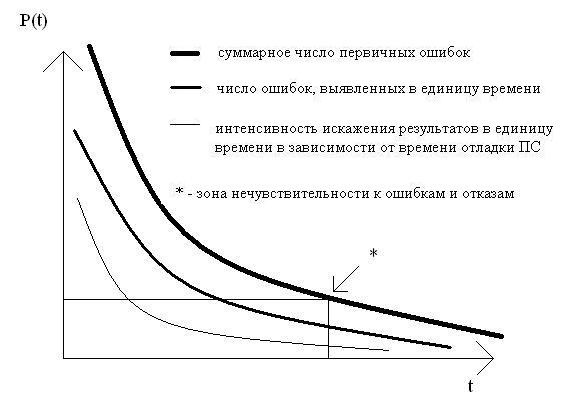
10. Математическая модель распределения ошибок в программах

где n₀ – число первичных ошибок, dn/dt – интенсивность обнаружения ошибок при отладке, K – некоторый коэффициент (характеризует изменение скорости появления искажений).

Интенсивность обнаружения ошибок в программе и абсолютное число устраненных первичных ошибок связаны уравнением:

.

При t = 0 решение этого уравнения имеет вид:

.

Число оставшихся в комплексе ПО ошибок:

.

Математические модели предназначены для приближенной оценки:

• Потенциально возможной надежности функционирования ПС в процессе испытания и эксплуатации.

• Числа ошибок, оставшихся не выявленными в анализируемых программах.

• Времени тестирования, требующегося для обнаружения ошибки в функционирующей программе.

• Времени, необходимого для выявления всех имеющихся ошибок с заданной вероятностью.

11. Простая интуитивная модель надежности по

ПО тестируется независимо двумя группами, каждая из которых разрабатывает независимые тесты. В течение некоторого времени группы работают раздельно, затем результаты сравниваются.

Пусть N ­– множество всех ошибок; N₁ – множество ошибок, выявленное первой группой; N₂ – множество ошибок, выявленное второй группой; N₁₂ – пересечение множеств N₁ и N₂.

Эффективность обнаружения ошибок каждой из групп E₁=N₁/N, E₂=N₂/N.

Интуитивное предположение: E₁ = N₁/N = N₁₂/N₂ =>

N = N₁₂ / (E₁E₂).

Последнее соотношение позволяет оценить количество ошибок в программном продукте.

В среднем считается, что в ПО одна ошибка на 100 операций.

Пример. N₁ = 20, N₂ = 30, N₁₂ = 8. E₁ = N₁₂/N₂, E₂ = N₁₂/N₁, E₁ = N₁₂/N₂ => N = 74.

12. Функция риска в теории надежности по

Количество оставшихся в программе ошибок – это количество ошибок, которые потенциально могут быть обнаружены на последующих стадиях жизненного цикла программы, после исправлений, внесенных в программу на текущей стадии ее жизненного цикла. Это количество оставшихся в программе ошибок – один из важнейших показателей надежности ПО.

Пусть P(t) – вероятность того, что ни одной ошибки не будет обнаружено на временном интервале [0,t]. Тогда вероятность хотя бы одного отказа за этот период будет Q(t) = 1 – P(t), и плотность вероятности можно записать как

Рассмотрим функцию риска R(t) как условную плотность вероятности отказа программы в момент времени t, при условии, что до этого момента отказов не было

Функция риска имеет размерность [1/время] и она очень полезна при классификации основных распределений отказов. Распределения с возрастающей функцией риска соответствуют тем ситуациям, когда статистические характеристики надежности ухудшаются со временем. И наоборот, распределения с убывающей функцией риска соответствуют обратной ситуации, когда надежность улучшается со временем в результате процесса обнаружения и коррекции ошибок.

Из последнего выражения ясно, что , и, следовательно,

, или

Данное равенство является одним из самых важных в теории надежности. Различные виды поведения функции риска во времени порождают различные возможности для построения моделей надежности ПО. Интенсивность обнаружения ошибок (функция риска), вместе с вероятностью безотказной работы программы и количеством оставшихся в программе ошибок, являются важнейшими показателями надежности программ.