Показатели, характеризующие спрос:

• структура спроса по разным признакам: степень удовлетворения, по месту покупки и т.д. Используются модели, связанные с методом группировки.

• потребительский потенциал, т.е. емкость рынка услуг;

• эластичность спроса, используется коэффициент эластичности.

3. Показатели, характеризующие пропорциональность рынка:

• соотношение спроса и предложения. Для анализа используются графические методы и методы математического анализа;

• структура рынков;

• структура товарооборота;

• структура продавцов по формам собственности;

• доля между оптовыми и розничными продавцами;

• региональность структуры рынка.

4. Показатели тенденции развития рынка:

• темпы роста продаж;

• векторы-параметры объемов продаж;

• параметры трендов товарных запасов и цен;

• тренды инвестиций и прибыли.

5. Показатели колеблемости, устойчивости и цикличности рынка:

• коэффициенты вариации продаж, цен и товарных запасов во времени и пространстве;

• индексы сезонности.

6. Показатели, характеризующие региональные различия:

• региональные вариации по отношению к спросу и предложению;

• региональные вариации уровня спроса;

• региональные вариации динамики основных показателей.

Для анализа используются динамики Фурье, параболы.

7. Показатели коммерческого риска:

• инвестиционный риск;

• маркетинговый риск;

• риск случайных рыночных колебаний;

8. Показатели деловой активности:

• портфель заказов;

• состав портфеля заказов;

• динамика;

• число, размер, частота, динамика сделок;

• степень загруженности производственных и торговых мощностей.

9. Показатели, характеризующие масштаб монополизации и конкуренции рынка:

• число фирм, их распределение на рынках каждого товара;

• общий объем реализации товара;

• доли государственных предприятий в общем объеме рынка;

• доли малых, средних и крупных фирм в общем объеме рынка.

При качественном анализе ситуации используются такие показатели как сбалансированный рынок, высокая конъюнктура, низкая конъюнктура, резкие колебания цен, дефицит, кризис сбыта.

В качестве инструментов измерения количественной оценки используются так называемые конъюнктурные индикаторы: цены, товарные запасы.

При анализе риска он подразделяется на:

• риски продавца;

• риски покупателя;

• риски инвесторов;

• риски торговцев;

• риски полной или частичной потери вложенных средств;

• риски обанкротиться и быть вытесненным с рынка;

• риски забастовки и т.д.

Наиболее распространенными методами оценки риска являются экспертные балльные оценки факторов и критериев риска. Каждый фактор риска оценивается в баллах, как правило, от 1 до 10. Каждому фактору присваивается вес, а сумма весов равна 1. Оценка равна сумме произведений факторов на вес по всем факторам риска – это аддитивная зависимость. Чем ближе оценка к единице, тем меньше риск, чем ближе к 10, тем больше риск.

При анализе потенциала рынка учитывается количество производственных или потребительских единиц, их мощность, эластичность спроса или предложения и другие факторы.

Емкость рынка зависит от численности i-той группы потребителей, норматива потребления i-той группы потребителей, эластичности спроса по ценам и доходам, насыщенности рынка, физического и морального износа, доли конкурентов на рынке.

При анализе пропорциональности развития рынка используется балансовый метод, индексный метод, коэффициент эластичности, трендовая модель, регрессионная модель. Особым показателем пропорциональности является компаративный индекс, позволяющий сравнивать динамические пропорции и являющийся одним из коэффициентов опережения, т.е. это соотношение темпов роста или темпов прироста. Например, отношение индекса продажи продуктов к индексу продажи услуг.

Основными методам анализа и прогнозирования рыночной конъюнктуры являются:

• экспертные методы;

• балансовые методы;

• методы анализа рядов динамики, т.е. выявление трендов, анализ колеблемости;

• индексный метод;

• методы классического и математического анализа;

• экспертные методы прогнозирования;

• прогнозирование по трендам;

• прогнозирование при помощи многофакторной регрессии.

16. Планирование маркетинговой и ценовой политики.

В основе планирования маркетинговой политики стоит выбор маркетинговых стратегий, которые можно назвать целевым стратегическим планированием.

При выборе маркетинговых стратегий используются две группы методов:

• методы, связанные с генерацией стратегий;

• методы, связанные с выбором оптимальной стратегии.

Для генерации стратегий можно использовать:

• морфологические методы;

• методы мозгового штурма;

• методы сценария;

• матричные методы (табличные).

Методы выбора оптимальной стратегии:

• метод анализа иерархий (самый эффективный, который включает в себя экспертные оценки);

• экспертный метод.

Матричные методы.

1. Матрица Ансоффа предназначена для генерации стратегий в условиях растущего рынка. Исходным пунктом модели является расхождение между реальным и планируемым развитием предприятия, так называемый целевой люк. Это значит, что цели предприятия не достижимы с помощью прежних стратегий.

Матрица называется "Продукт-рынок". По строкам откладываются продукты, по столбцам – рынки. Матрица размером 2*2. Продукты, как и рынки, могут быть имеющиеся и новые. В матрице элементы имеют следующее значение:

• a₁₁ – расширение рынка – увеличение доли рынка или объемов продаж с помощью снижения цен, улучшения качества, привлечения покупателей конкурирующей продукции, рекламы;

• a₁₂ – элемент развития рынка – выход со старыми продуктами на новые рынки. Методы: глобализация, расширение функций продуктов, новая область применения и т.д.;

• a₂₁ – элемент развитие продукта или инновация – новые продукты на рынке, квазиновые продукты, продуты новые только для предприятия;

• a₂₂ – элемент диверсификация – предприятие переходит к новым формам деятельности. Различают три формы диверсификации:

• горизонтальная – производятся сходные изделия (например, автопредприятие производит мотоциклы);

• вертикальная – продукты связаны между собой производственным циклом (например, предприятие одежды начинает производить ткани);

• натуральная – новый продукт совершенно не связан со старым.

Каждая стратегия из четырех характеризуется каким-то набором оценочных параметров. Чтобы выбрать нужную, используются методы многокритериальной оптимизации. В некоторых случаях можно свести к одному критерию.

Преимущества матрицы:

• наглядное структурирование сложных реальных процессов;

• простота использования.

Недостаток ее заключается в том, что она односторонне ориентирована на рост.

2. Матрица Портера основана на концепции конкурентных стратегий. Портер выделил пять движущих сил конкуренции:

1. внутриотраслевая конкуренция;

2. угроза со стороны новых конкурентов;

3. сильная позиция поставщиков;

4. сильная позиция покупателей;

5. угроза со стороны продуктов-заменителей.

Матрица Портера состоит из четырех элементов. По строкам откладываются стратегические цели, по столбцам – стратегическое преимущество. В качестве стратегической цели выбирается либо вся отрасль, либо сегмент рынка. В качестве стратегического преимущества можно выбрать либо неповторимость продукта с точки зрения покупателя, либо преимущество в затратах.

Элементы матрицы, характеризующие стратегии:

• a₁₁ – дифференцирование;

• a₁₂ – лидерство в области затрат;

• a₂₁, a₂₂ – сегментирование рынка.

Основная идея стратегии дифференцирования состоит в том, что продукт должен отличаться от продукта конкурента, затраты при этом играют второстепенную роль. В стратегии о лидерстве в области затрат основная идея в сокращении затрат. Основная идея сегментации в работе с одним или несколькими сегментами рынка (например, избранные группы клиентов рынка, географическая ограниченность рынка).

3. Матрица "Рост рынка – доли рынка". Эта модель разработана американской фирмой Boston Consulting Group. По строкам записывается рост рынка: высокий или низкий, а по столбцам – доли рынка: высокая и низкая.

Элементы матрицы – стратегические бизнес-единицы (СБЕ), представляющие независимые друг от друга сферы деятельности предприятия, которые характеризуются особой рыночной задачей, связанной с клиентами, продуктами или группами продуктов, кругом клиентов. Различные СБЕ имеют различные шансы и риск.

Элементы матрицы:

• a₁₁ – условно называются "звезды", фирма находится в фазе роста жизненного цикла. Эти СБЕ приносят прибыль, которая идет на укрепление их собственных позиций на рынке;

• a₁₂ – так называемые "знаки вопроса". Для них характерны начальные фазы жизненного цикла, т.е. небольшая доля рынка, прибыль этих продуктов меньше затрат на расширение рынка;

• a₂₁ – так называемые "дойные коровы". Продукты, достигшие фазы зрелости, приносят большую прибыль. За счет них финансируются другие СБЕ.

• a₂₂ – так называемые "собаки". Не имеют высокой доли на рынке. Находятся в фазе насыщения и дегенерации.

4. Матрица "Привлекательность рынка – преимущество конкуренции". Модель разработана General Electric и др. фирмой.

Матрица размером 3*3. По строкам откладывается привлекательность: высокая, средняя и низкая, по столбцам – преимущества конкуренции: малые, средние и большие. Эта матрица позволяет выбрать следующие стратегии:

• a₁₃ – стратегия инвестиций и роста для СБЕ;

• a₃₁ – стратегии исчерпания для СБЕ (т.е. эти продукты надо свертывать);

Для других элементов стратегические решения принимаются в зависимости от ситуации.

Планирование ценовой политики.

Если предприятие входит в отрасль, то нужно рассчитывать затратные модели. Для расчета себестоимости единицы продукции задается некоторая нормативная рентабельность. Если цена больше рыночной, то с такой продукцией на рынок выходить нельзя, и наоборот. Когда отсутствует чистая конкуренция, то это случай монополии, монопсонии и двусторонней монополии.

Рассмотрим вопрос определения договорных цен в случае двусторонней монополии, т.е. когда один – изготовитель продукции, и один – потребитель. Монопсония – случай, когда потребитель один, а монополия – производитель один. Во всех этих случаях нужен договор о цене. Здесь можно использовать теорию игр, а именно кооперативные игры.

Двусторонняя монополия.

W₁^*, W₂^* – выигрыш изготовителя и потребителя в отсутствии договора;

V₁₂ – выигрыш коалиции;

W_i – выигрыш каждого игрока в коалиции.

Нужно определить, захотят ли изготовитель и потребитель заключить договор и, если да, то каковы условия договора.

Условием является свойство супераддитивности, основанном на оптимуме по Парето: . Условие говорит о том, что совместный выигрыш при заключении договора не меньше суммарного выигрыша по отдельности или что дополнительный совместный выигрыш при заключении договора должен быть больше нуля. Далее возникает вопрос, как распределить дополнительный совместный выигрыш. Он зависит от цены. Для распределения выигрыша в рамках игровой модели можно воспользоваться принципом оптимальности Нэша, который базируется на 6 аксиомах:

1. реализуемость;

2. индивидуальная рациональность;

3. оптимальность по Парето;

4. независимость от посторонних альтернатив;

5. линейность;

6. симметрия.

В результате получается единственное решение:

Обозначим – дополнительный совместный выигрыш, тогда:

Здесь реализуется принцип эгалитаризма или принцип равенства: не совместный выигрыш делится пополам, а совместный дополнительный выигрыш. Выигрышем предприятия является прибыль. Рассмотрим часть прибыли, которая зависит от цены. Прибыль изготовителя: , где – доля чистой прибыли. Прибыль потребителя: , где – норма амортизации. Предположим, что потребитель покупает оборудование, которое будет приносить доход, который с ценой не связан. С ценой связаны затраты на покупку и обслуживание.

Введем два понятия:

1. нижний предел цены или цена изготовителя P_S – это цена, при которой выигрыш при заключении сделки и без заключения равен ;

2. верхний предел цены или цена потребителя P_C – это цена, при которой выигрыш при заключении договора и без заключения договора равен .

В качестве выигрыша можно использовать рентабельность, среднюю рентабельность в течение реализации договора, NPV, равный сумме положительных и отрицательных финансовых потоков за время эксплуатации оборудования.

Далее можно определить договорную цену по Нэшу, учитывая, что дополнительная чистая прибыль изготовителя равна дополнительной чистой прибыли потребителя (т.е. дополнительный выигрыш делится пополам).

Подставив значение прибыли, получим:

Такая цена устанавливается, если изготовитель и потребитель соглашаются с принципом эгалитаризма.

Монопсония.

Пусть будет два изготовителя и один потребитель.

W₁^*, W₂^*, W₃^*– выигрыши договаривающихся сторон без заключения договора;

V_i3 – общий выигрыш коалиции потребителя с i-тым изготовителем (i=1,2);

W_i , W₃– выигрыш каждого игрока в коалиции.

В данной задаче возможны три коалиции:

• первый изготовитель и потребитель;

• второй изготовитель и потребитель;

• первый и второй изготовители и потребитель.

Возможность образования первых двух коалиций связано со свойством супераддитивности:

Здесь возможны следующие варианты. Если ни одно из условий не выполняется, то договор не будет заключен вообще. Если выполняется одно условие из двух, то в этом случае имеем дело с двусторонней монополией. Если выполняются оба условия, то коалиция создается с тем, где больше совместный дополнительный выигрыш. Пусть с первым изготовителем совместный дополнительный выигрыш будет больше. Обозначим дополнительный совместный выигрыш через .

– условие выбора коалиции с первым изготовителем.

Здесь возможна конкуренция, т.к. изготовителей уже два. В условиях конкуренции цена снижается. Рассмотрим этот случай. Потребитель может потребовать некоторые преимущества, т.к. у него есть альтернатива. Он может объявить, что дополнительный выигрыш с первым изготовителем равен , т.е. то, что будет делиться, уменьшится. Потребитель может заявить, что он заключит договор со вторым изготовителем и получит выигрыш , т.е. цена потребителя изменится. Возможно два варианта:

1. каждый изготовитель может полностью обеспечить потребности покупателя. Тогда делится пополам:

Цена изготовителя меньше цены потребителя. Цена падает за счет конкуренции.

2. один изготовитель полностью обеспечить не может потребности покупателя. Тогда сначала заключается договор с первым изготовителем по принципу описанному выше. Но так как его потребности удовлетворены не полностью, то затем договор заключается со вторым изготовителем. Тогда изменятся начальные условия, а именно цена потребителя:

т.о. увеличивается начальный выигрыш, т.е. выигрыш без заключения договора, тогда изменится и цена потребителя:

Цена с первым и вторым изготовителями:

Цены будут разными. Цена больше со вторым изготовителем, т.к. у него меньше эффективность.

Рассмотрим случай, когда не два изготовителя, а больше. Пронумеруем их в порядке убывания совместного выигрыша. Если первый изготовитель может обеспечить потребности покупателя полностью, то договорная цена определяется, как и в случае с двумя изготовителями. Если же не полностью, то договор заключается с несколькими изготовителями по разным ценам:

и с остальными:

Монополия.

Рассматривается случай с одним изготовителем и несколькими потребителями. Цена здесь будет возрастать в отличие от предыдущего случая.

Если имеется один изготовитель и два потребителя, то:

1. первый изготовитель может обеспечить двух потребителей, следовательно, будут разные цены для двух потребителей:

Цена P₂ будет выше, т.к. второй потребитель менее эффективен.

2. изготовитель не может обеспечить полностью потребителей. Тогда возникает конкуренция и договор заключается с первым потребителем, т.к. он более эффективен:

Теперь рассмотрим случай, когда потребителей больше двух:

1. Изготовитель обеспечивает всех потребителей. Потребители нумеруются в порядке убывания совместного выигрыша и покупают продукцию по разным ценам. Число потребителей не бесконечно, а достаточно мало, т.е. ситуация не рыночная:

и с остальными:

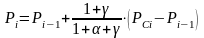
2. изготовитель не может обеспечить всех потребителей. Предположим, что он может обеспечить m из n потребителей:

17. Моделирование инвестиций и анализ их эффективности.

С математической точки зрения, в данном случае можно использовать несколько методов:

1. метод дерева решений, метод графа решений;

2. метод статистических испытаний Монте-Карло, т.е. эта модель имитационно-статистическая.

При составлении и разработке инвестиционного проекта необходимо оценить два основных его параметра, которые взаимосвязаны. Это эффективность и риск. В качестве эффективности можно использовать так называемый NPV – чистый приведенный продукт. Существует такое понятие как опасность, а ее количественная мера – это риск. Таким образом, под риском следует понимать вероятность неблагоприятного исхода. Можно использовать коэффициент вариации, т.е. правило трех сигм. Обычно чем эффективнее проект, тем больше риск.

Рассмотрим первую модель немного подробнее. Она имеет следующие стадии:

1. прединвестиционные исследования или бизнес план. Возможные исходы:

   • решение о продолжении проекта;

   • решение об остановке проекта.

2. техническая реализация проекта – создание опытного образца. Возможные исходы:

   • отказ от продолжения проекта (например, обнаружено, что затраты большие или выявлены технические сложности);

   • реализация, требующая увеличения сроков или затрат;

   • реализация в соответствии с техническим заданием.

3. техническая подготовка производства. Возможные исходы:

   • невозможность производства серийного продукта;

   • подготовка производства;

   • выпуск инвестиционного продукта.

4. производство инвестиционного продукта. Возможные исходы:

   • производство завершается выпуском первой партии (первого образца), в связи с отказом потребителя от товара;

   • производство различными объемами.

5. эксплуатация (использование) инвестиционного продукта.

Эти стадии можно представить в виде ребер графа, а исходы – в виде вершин. На ребрах могут указываться оценки вероятности того или иного исхода. Следует помнить, что сумма вероятностей должна равняться 1.

С помощью графа можно оценить средневзвешенную эффективность проекта, где веса – это вероятности исходов. Интегральный эффект Э_инт, средний взвешенный по вероятностям отдельных решений, будет равен:

где Э_i – эффект i-го исхода;

Р_i – вероятность i-го исхода.

В качестве показателя оценки эффективности рассмотрим суммарный финансовый поток, который состоит из:

• положительного финансового потока;

• отрицательного финансового потока.

Граф следует представлять в виде динамической инвестиционной модели, т.е. учитывать процесс во времени, т.к. деньги изменяют свою стоимость. Имитируется вложение денег в банк.

Рассмотрим подход, связанный с NPV, который учитывает изменение стоимости денег при помощи дисконтирования. В качестве дисконта используется величина: , где r_бр – безрисковая ставка. Т.к. мы не получаем доход от банковских процентов, то деньги уменьшаются, т.е.

, где i – номер исхода,

, иначе это называется ожидаемый показатель.

Далее нужно сравнить ожидаемый показатель с затратами, где сумма всех отрицательных потоков – это сумма на всех этапах, кроме последнего.

При таком подходе риск оценить сложно.

Рассмотрим вторую модель – метод испытаний Монте-Карло. Его суть состоит в том, что объект можно представить в виде серого ящика, имеющим входные параметры и один или несколько выходных параметров. Нам известен алгоритм преобразования входов и выходов, но, зная значения входных параметров, аналитически определить выходные параметры нельзя. Здесь используется метод статистических испытаний. Предположим, что входные параметры заданы в виде распределения. Случайный характер могут носить затраты на разных стадиях: затраты на разработку, реализацию, производство. Отсюда можно оценить закон распределения. Кроме того, при эксплуатации инвестиционного проекта случайными величинами могут быть также цены и спрос, т.е. объемы продаж тоже, что также можно представить их законами распределения.

Далее проводится ряд опытов. Чем их больше, тем точнее получится модель (900, 1000…). В каждом эксперименте при помощи датчика случайных чисел мы получаем конкретные значения – показатели на входе. Зная алгоритм преобразования входа и выхода, находим выход. В нашем случае выход – NPV.

Каждому опыту соответствует определенное значение NPV. Затем следует упорядочить полученные значения, построить интервальный ряд и гистограмму. По ней можно подобрать уже теоретический закон распределения, который позволяет определить, какие критерии используются для непараметрических гипотез.

Имитационная модель учитывает также взаи­мосвязи некоторых переменных, основанные на закономерностях рынка. В частности:

1. Взаимосвязь цены и объемов продаж (Q(P)):

где Q₀ – объем продаж инвестиционного про­дукта, соответствующий математическое ожиданию цены (Ц₀),

– относительное изменение цены;

E_p – коэффициент эластичности спроса на инвестиционный продукт по цене. (Для систем регулирования подачи тепловой энергии принято E_p=2)

2. Зависимость издержек от объемов производства:

где – относительное изменение объема продаж;

d – постоянный коэффициент, зависящий от структуры издержек.

В данной модели можно также оценить следующие характеристики совокупности: среднее значение, показатели вариации, средне квадратическое отклонение, квантили. Также можно оценить каким-либо образом риск – это соотношение среднего значения и среднеквадратического отклонения, т.е. показателей вариации. В нашем случае риск – это отрицательное значение NPV.

Достоинством этой модели является – более полная информация, а первой – простота.

18. Модели развития и размещения производства.

В качестве критерия выбираются минимальные затраты по производству и транспортировке. Это записывается в виде целевой функции. В качестве ограничений выступают ограничения по различным ресурсам.

Затем задача решается методом математического программирования.

Также в качестве критерия можно выбрать максимум загрузки мощностей. Однако с такой постановкой задачи модель становится очень сложной, что затрудняет ее решение и анализ. Поэтому иногда целесообразно разбивать модель на ряд этапов.

Рассмотрим пример, который связан с размещением и развитием производства электронной продукции на предприятиях корпорации. Особенность электронного продукта заключается в том, что затраты на перевозку значительно меньше затрат на производство. Соответственно вначале целесообразно не учитывать затраты на перевозку.

Объект – корпорация, состоящая из множества предприятий. Наша задача – спланировать производство однородной продукции, выпускаемой на предприятиях корпорации.

– предприятия корпорации;

– виды комплектующих или стадии производства;

m_i,j – производственные мощности i- того предприятия по j-тому процессу;

с_ij – себестоимость j-того комплектующего на i- том предприятии;

m_i,j+1 – максимальное количество комплектующих, которое может быть получено со стороны;

x_ij – количество комплектующих j-того вида, которые производятся на i-том предприятии;

q – количество готовых изделий, которое не должно превышать q_max – максимально определенного маркетинговыми исследованиями.

На первом шаге необходимо определить максимально возможный выпуск. Надо найти узкое место: с учетом внешних поставщиков, т.е. надо учесть m_i,j+1. Если найденное (спрос), то оно не меняется, если же превышает, то меняется на q_max.

На втором шаге определяется задача размещения, т.е. на каком предприятии сколько комплектующих выпускать. Эту задачу надо решать для каждого вида комплектующих. В узком месте все производственные мощности должны быть загружены. Как быть с другими комплектующими, отличных от узких мест?

В качестве критерия выбираются затраты на производство, которые должны быть минимизированы:

Ограничения: , .

На третьем шаге необходимо решить задачу развития производства. Предположим, что у корпорации есть финансовые средства, которые можно вложить в производство. Задачу имеет смысл решать, т.е. дальше развивать корпорацию, если рынок не насыщен.

Возникает вопрос: куда в первую очередь вкладывать средства, т.е. определить, на каком предприятии, в какое комплектующее вкладывать и размер вложений. Ответить можно следующим образом:

1. надо вкладывать в "узкое место" (т.е. определить номер комплектующего),

где Y – прирост объема производства; a_ij = M_ij – X_ij – "узкое место"; K_ij – капитальные вложения; K_удij – значения удельных капитальных вложений, необходимых для прироста мощностей на единицу. Прирост объема производства (Y) должен обеспечивать минимальные затраты.

2. в качестве критерия для определения номера предприятия нужно учитывать условие максимизации фондоотдачи, т.е. меньшие удельные капитальные вложения:

, где

Здесь обозначим индекс мощностей S, которые первоначально оказались полностью загружены. Объем капитальных вложений должен быть таким, чтобы прирост мощностей по S-му элементу стал соответствовать “узкому месту” по прочим элементам.

3. чтобы определить размер вложений, надо свободные производственные мощности предприятия (не загруженные при выпуске конечной продукции в количестве Z шт.) умножить на величину кап. вложений:

И так далее до тех пор, пока:

• не загрузим мощности по всем комплектующим одинаково;

• не насытим рынок;

• не кончатся деньги.

Теперь надо решить транспортную задачу, т.е. минимизировать транспортные издержки.

Есть поставщики и покупатели однородной продукции. Нужно определить, кто поставщик, а кто – потребитель. Если разница между комплектующими и сборкой больше нуля, то данное предприятие – поставщик, если меньше нуля – то потребитель. Затраты же от внешних поставщиков равны нулю. Далее решается транспортная задача.

19. Планирование и оптимизация работы предприятия.

Рассмотрим задачу оптимизации производственной программы. Предполагается, что предприятие выпускает различные виды изделий: .

Производственная программа представляет собой годовой план выпуска.

x_ij – количество изделий j- того вида, которое является неизвестным.

Критерием работы предприятия является максимизация прибыли (также может быть минимизация затрат, максимизация выручки, выпуска продукции).

Ограничения по факторам производства (Т, З, К). Ограничение по капиталу должно быть обязательно. Ограничения относительно оборудования удобно рассматривать по фонду времени работы оборудования. По каждой группе оборудования считается свой фонд времени. Это главное ограничение, которое всегда присутствует в оптимизации производственной программы.

Ограничение по выпуску определяется при помощи маркетинговых исследований – ограничение по рынку сбыта и точке безубыточности.

Целевая функция может иметь вид:

• Максимум прибыли, получаемой от реализации продукции:

где P_j – цена j-го изделия,

С_j – себестоимость j-го изделия,

X_j – выпуск j-го изделия (в шт.)

• Минимум себестоимости товарного выпуска:

• Максимум объема реализованной продукции:

• Если затраты разделить на переменные и постоянные, то функция прибыли примет вид:

где AVC_j – переменные издержки производства j-го изделия,

AFC – постоянные издержки производства.

С точки зрения линейной модели последняя запись прибыли более корректна.

Ограничения:

• по точке безубыточности имеют вид:

, т.е.

• по рынку сбыта: . Два ограничения по точке безубыточности и по рынку сбыта составляют ограничение по выпуску.

• по фонду времени работы оборудования:

Где T_ij – трудоемкость;

T_i – фонд времени работы i – той группы оборудования;

• по материалам:

где T_ij – норма расхода i-го материала на производство единицы j-го изделия,

A_i – максимальный запас i-го материала.

Задача решается симплекс-методом. Для этого необходимо привести уравнение к каноническому виду, т.е. ограничения из неравенств следует привести к равенствам, вводя в левую часть дополнительную переменную x_n+1, т.е. при ограничениях типа

, , ,

получаем:

a_i1 * x₁ + a_i2 * x₂ +…+ a_in * x_n + x_n+1 = b_i

a_i1 * x₁ + a_i2 * x₂ +…+ a_in * x_n – x_n+1 = b_i

Но для решения задачи на ЭВМ необходимо, чтобы новая переменная имела при себе коэффициент "+1", поэтому все второе выражение умножаем на "-1" и получаем:

- a_i1 * x₁ - a_i2 * x₂ -…- a_in * x_n + x_n+1 = - b_i

С каждой задачей линейного программирования связана другая линей­ная задача, называемая двойственной. Связь исходной и двойственной за­дачи в том, что решение одной из них может быть получено из решения другой. Решение двойственной задачи позволяет более глубоко проанали­зировать результаты.

Пусть предприятие выпускает видов продукции. Цена – P_j (в руб), выпуск – X_j (шт), расход i-го материала на производство j-го из­делия – a_ij. Тогда модель исходной задачи на максимум товарной продук­ции будет иметь вид:

,

Для этого же предприятия можно сформулировать и двойственную за­дачу. Требуется найти такие оценки ресурсов Y_j (руб/кг), которые обес­печивали бы минимум общего расхода ресурсов в стоимостном выражении, а затраты на производство каждого вида продукции не были бы меньше его цены, т.е.

Прямая задача является задачей на max, а двойственная - на min. параметры целевой функции исходной задачи являются ограничениями двойственной задачи. Ограничения исходной задачи являются параметрами целевой функции двойственной задачи. Матрица коэффициентов a_ij исход­ной задачи транспонируется в двойственной задаче. Переменные Y_i назы­ваются оценками или учетными, неявными ценами ресурсов.

С математической точки зрения, двойственная оценка показывает, на сколько изменится целевая функция при изменении соответствующих ограничений на малую единицу.

Свойства двойственных оценок:

Свойство 1. 1) Если , то X_n+1 = 0 , где X_n+1 – количество неизрасходованного ресурса, то данное выражение имеет следующий экономический смысл. Если ресурс расходуется полностью (равенство в ограничении), то он является дефицитным и его двойственная оценка, т.е. цена, больше нуля. Чем более дефицитен ресурс, тем больше двойственная оценка.

2) Если , то X_n+1 > 0, . Экономический смысл: если ресурс расходуется не полностью, то его двойственная (или неявная) оценка равна нулю.

Свойство 2. 1) Если , то . Экономический смысл: если издержки равны цене, то данная продукция выпускается, она выгодна (издержки измеряются в неявных ценах).

2) Если, то . Экономический смысл: поскольку издержки больше цены, то изделие не выпускается.

Свойство 3. Для оптимального плана , т.е. затраты на ресурсы равны стоимости товарной продукции. Для неоптимального плана:

При решении задачи для определения производственной программы нужно выявить выгодную и невыгодную продукцию, чтобы сделать ее выгодной. Также нужно выявить узкое место, используя свойство 1.

Если рассматривать случай, когда затраты на единицу продукции c_j зависят от выпуска, то получим нелинейные целевую функцию и ограничения, таким образом, имеем задачу нелинейного программирования. Для решения следует применять метод множителей Лагранжа. Но практическую значимость имеет линейное программирование (оно снижает нелинейность). Округлять следует при решении в меньшую сторону, т.к. имеются ограничения на ресурсы.

20. Модели многокритериальной оптимизации.

В процессе принятия решений одним из составляющих является выбор альтернатив или вариантов. При выборе альтернатив используют различные языки. Наиболее распространенным является критериальный язык выбора альтернатив, который заключается в том, что каждой альтернативе ставится в соответствие некоторое число. Есть множество X альтернатив, где x_j, – различные альтернативы.

Каждой альтернативе ставится в соответствие Q(x_j). Оптимальное значение может определяться как максимальное значение критерия:

Кроме критериального языка существует язык бинарных отношений. Но в основном пользуются критеральным языком выбора: Q(x_i), , где i – номер критерия.

Случаи использования моделей многокритериальной оптимизации:

1. Система, являющаяся объектом рассмотрения, характеризуется критерием набора параметров, часть из которых противоречивы.

2. Имеется один глобальный критерий С, как правило неколичественный, сравнение и выбор альтернатив по которому затруднено. Вследствие чего происходит декомпозиция глобального критерия на локальный, по которому сравниваются альтернативы. Этот случай используется на макроэкономическом уровне.

3. При кооперативном принятии решений имеет место добровольное взаимоотношение субъектов, когда они договариваются.

Основные подходы:

1. группа методов, связанных с выдвижением аксиом ведущим функциям полезности, а аксиома проверяется лицами, принимающими решение;

2. группа методов, при использовании которых руководители непосредственно назначают вид зависимости по оценкам между различными критериями;

3. методы поэтапного определения компромисса между оценками различных критериев;

4. методы сравнения альтернатив с использованием порогов несравнимости;

5. человеко-машинные методы принятия решений по поиску лучшей альтернативы.

Вторая классификация выделяет следующие группы методов:

1. лексикографическое упорядочивание;

2. сравнение разностей критериальных оценок;

3. метод идеальной точки;

4. методы эффективность-стоимость;

5. методы свертки на иерархии критериев;

6. методы порогов независимости;

7. методы кривых безразличия;

8. методы анализа иерархий;

9. методы теории нечетких множеств;

10. методы теории ожидаемой полезности.

Третья классификация:

1. принцип равномерности;

2. принцип абсолютной уступки;

3. принцип относительной уступки;

4. принцип выделения главного критерия;

5. принцип последовательной уступки.

На основе сравнительного анализа различных подходов может быть предложена следующая классификация методов многокритериальной оптимизации:

1. Выделение множества Парето. Метод заключается в попарном сравнении альтернатив на основе выбранного бинарного отношения (например, отношения доминирования). Причем альтернативы, не худшие по всем критериям, выделяются в множество, называемым ядром. Если бинарное отношение является таким, при котором одна альтернатива имеет по всем критериям не худшие, а хотя бы по одному, лучшие оценки, то выделенное ядро называется множеством Парето.

2. Условная оптимизация. Метод основан на предположении, что можно выделить один главный критерий, а остальные использовать как ограничения. Тогда задача выбора оптимального варианта формулируется как задача нахождения основного критерия:

при условии, что ,

3. Введение суперкритерия. Данный метод предполагает свертку критериев, т.е. введение скалярной функции векторного аргумента:

При определении вида функции f(Q(X)) можно использовать аксиоматический подход. Однако в большинстве случаев принятие аксиомы на практике разрушается. Лучше использовать прямое задание функции f(Q(X)).

Наиболее часто используют следующие виды функции:

1. Максиминная свертка основана на принципе эгалитаризма и ведет к увеличению уровня минимального или наихудшего критерия. Принцип эгалитаризма состоит в следующем: если у субъектов существуют оценки полезности, тот этот принцип максимизирует полезность наиболее слабого субъекта. Если нет ограничений, в частном случае, тот этот принцип приводит к равенству полезностей:

При этом предполагается, что Q_i(x) пронормированны.

2. Аддитивная свертка основана на принципе утилитаризма и ведет к увеличению суммарной полезности, соответствует принципу абсолютной уступки, может допускать резкую дифференциацию критериев. Так называемое высокое значение суперкритерия может быть получено за счет высокого уровня одних локальных критериев при низких уровнях других критериев.

, где - вес i – ого критерия.

Похожий результат дает метод анализа иерархий в случае трехуровневой иерархии, где цель разбивается на критерии.

Это граф со слабыми связями, , , q_i – критерии, x_j – альтернативные варианты.

Метод анализа иерархий предполагает последовательную оценку влияния элементов нижнего уровня на элементы верхнего уровня. В результате получается оценка влияния каждого элемента самого нижнего уровня на общую цель. Соответственно выбирается та альтернатива в качестве наилучшей, влияние которой на общую цель максимально.

Влияние элементов нижнего уровня на верхний оценивается при помощи матрицы сравнения А: a_ij = 1/a_ji, что показывает уровень преобладания влияния элемента i над элементом j на элемент высшего уровня. Для оценки a_ij используется шкала отношений с нечетными цифрами от 1 до 9, где 1 – одинаковая значимость, одинаковое влияние, 9 – максимальное различие. При обработке матрицы А получается вектор приоритетов альтернатив, представляющий собой собственный вектор W матрицы A, что определяется по рекуррентному соотношению:

где Е – единичный вектор; k – номер итерации; С – константа.

Процесс продолжается до выполнения условия:

, где – зафиксированная погрешность.

При k=1 .

Для альтернатив x компоненты векторов-приоритетов в нашем случае будут являться пронормированными значениями критерия Q_i(x). Аналогично определяются веса критериев. Составляется матрица парных сравнений для критериев. Компоненты векторов-приоритетов будут являться весами критерия . Результирующий вектор приоритетов относительно цели определяется следующим образом:

Первая матрица получается следующим образом: друг за другом записываются вектора приоритетов для каждого критерия.

При парном сравнении Q_i(x) должно быть предварительно проранжированны:

.

Обобщенная формула нахождения степени влияния любого j-го элемента n-го уровня на общую цель выглядит:

где k – число элементов в n-1 уровне; C_i0 – степени влияния элементов n-1 уровня на общую цель;C_ji – степени влияния j-го элемента n-го уровня на элементы n-1 уровня.

В результате полученный при трехуровневой иерархии критерий аналогичен аддитивной свертке. Метод иерархий при трехуровневой свертке имеет достоинство: удобство оценивания альтернатив (для оценивания может использоваться как попарное сравнение, так и критерий). Кроме того, предполагается при анализе иерархий автоматическое нормирование и использование при необходимости большего числа уровней для анализа иерархий.

3. Мультипликативная свертка основана на принципе относительной уступки, которая снижает цену уступки для локальных критериев с большей величиной. Этот принцип близок принципу эгалитаризма. Этот вид свертки – что-то среднее между максиминной сверткой и аддитивной, но все же ближе к максиминной:

Все методы прямого оценивания предполагают нормирование критерия. Используются следующие способы нормирования:

1. Вводится понятие идеального качества операции Q_{i норм}(X): . В качестве идеального вектора выбираются заданные величины критериев, которые задаем сами.

2. В качестве идеального вектора выбирается вектор, компонентами которого являются максимально возможные величины критериев Q_i(X).

3. В качестве идеального вектора берется максимально возможный разброс вектора, т.е. разница между максимальным и минимальным значениями.

4. Расчет компонентов вектора приоритетов.

4. Поиск альтернативы с заданными свойствами. Этот метод используется в том случае, если заранее могут быть заданы значения локальных критериев , называемые уравнениями притязания. Задача в этом случае сводится к приближению к идеальной точке в m-мерном пространстве с использованием числовой меры близости.

Например:

Модель Парето-Лоренца-Джини.

Кривая Лоренца

По закону Парето-Лоренца-Джини, чем больше доход, тем меньше людей его имеют. На графике кривой Лоренца по оси абсцисс откладываются квинтильные точки, по оси ординат – процентный уровень дохода. При равномерном распределении доходов каждая двадцатипроцентная группа населения имела бы пятую часть доходов общества. На графике это изображается диагональю квадрата и рассматривается как линия равномерного распределения, т.е. при равномерном распределении коэффициент Джини равен 0. При неравномерном распределении "линия концентрации" представляет собой вогнутую вниз кривую. Чем больше отклонение кривой Лоренца от диагонали квадрата, тем выше поляризация доходов общества.

Если рассматривать кривую, то коэффициент Джини можно рассчитывается по формуле, где – доля населения в интервале, – доля доходов у этой доли населения, cumy_i – кумулята, т.е. накопленный доход, где n – число интервалов.

Децильные коэффициенты дифференциации доходов показывают отношение минимального дохода 10 % самых богатых к максимальному доходу 10 % самых бедных.

Коэффициент фондов, во сколько раз среднедушевой доход 10 % наиболее высокодоходного населения больше, чем у 10 % населения с наименьшими доходами.

21. Хаотическая динамика. Примеры хаотических систем.

Тео́рия ха́оса — математический аппарат, описывающий поведение некоторых нелинейных динамических систем, подверженных при определённых условиях явлению, известному как хаос. Поведение такой системы кажется случайным, даже если модель, описывающая систему, является детерминированной.

Примерами подобных систем являются атмосфера, турбулентные потоки, биологические популяции, общество как система коммуникаций и его подсистемы: экономические, политические и другие социальные системы. Их изучение, наряду с аналитическим исследованием имеющихся рекуррентных соотношений, обычно сопровождается математическим моделированием, эффект Коновала — распределение частот выпадения положительных результатов, или принятия правильных решений.

Теория хаоса — область исследований, связывающая математику и физику.

Динамическая система, процессы в которой характеризуются странным аттрактором, является хаотической системой. Динамическая система хаотична тогда и только тогда, когда у нее существует незамкнутая фазовая траектория. В отличие от устойчивой динамической системы определить состояние хаотической системы по заданным значениям времени и начальных условий невозможно.

Приведем примеры моделей хаотических систем.

1. / = + - ,

=- ,

=- - ( ) ,

где ( )= 0 при 0 и ( )=1 при 0.

2. Система уравнений Лоренца — трехмерная система нелинейных дифференциальных уравнений первого порядка вида

/ = – + ,

/ = – + – , (1)

3/ = –

В ней s, b и r — параметры. Эта система возникла в задаче о моделировании конвективного течения жидкости, подогреваемой снизу. Такое течение описывается системой дифференциальных уравнений в частных производных. Система (1) получается из нее проектированием на специальное трехмерное подпространство.

В результате численного интегрирования системы (1) Э. Лоренц обнаружил, что при s = 10, b = 8/3 и r = 28 у этой динамической системы, с одной стороны, наблюдается хаотическое, нерегулярное поведение всех траекторий и все траектории притягиваются к аттрактору рис. 1. На рис. 2 приведена зависимость от времени.

Рис. 1.  Пример странного аттрактора (для задачи Лоренца)

Рис. 2.  Хаотические колебания (зависимость переменной x₁ от времени в задаче Лоренца)

22. Переход к динамическому хаосу в классических трехмерных диссипативных системах обыкновенных дифференциальных уравнений. Системы Лоренца, Ресслера, Чуа, Магницкого. Многомерные нелинейные системы обыкновенных дифференциальных уравнений.

СИСТЕМА ЛОРЕНЦА. dx/dt= -a*x+a*y ,     a>0 dy/dt= r*x-y-x*z,       r>0 dz/dt= -b*z+x*y,        b>0

Уравнения подвергались всестороннему изучению многими авторами, начиная с Лоренца, который проинтегрировал их численно, используя фиксированные значения управляющих параметров a =10, b=8/3 и единственный переменный управляющий параметр r.            При 0< r<1 (рис.1) имеем только одну критическую точку. Она является одновременно локальным и глобальным аттрактором. Другими словами, любое начальное состояние будет приближаться к началу координат при t стремящемся к бесконечности. Когда r становится близким к единице, возникает критическое замедление, а при достижении величиной r значения +1 начало координат теряет устойчивость и от него ответвляются два аттрактора, причем оба глобально и локально устойчивы. В случае r<1.345 равновесия - узлы, r >1.345 - фокусы.          При увеличении r до величины 13.926 две неустойчивые траектории, исходящие из начала координат, возвращаются в начало координат при t стремящемся к бесконечности, при этом перестают быть глобальными аттракторами. Напротив, они окружены; окрестностями, в которых являются локальными. Точка, исходящая из области, лежащей вне этих окрестностей, может совершать колебательные движения из одной окрестности в другую и обратно. Такое поведение называют метастабильным хаосом (рис.2).         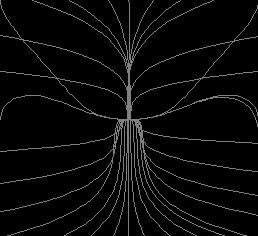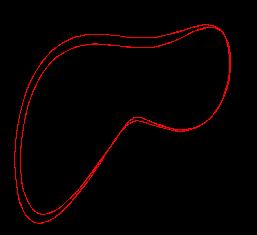При r =24.74 возникает инверсия бифуркации Хопфа, при r > 24.74 остается "странный аттрактор" (рис.3). При больших r в системе существует симметричный цикл (рис.6 - r=400). Далее при уменьшении параметра происходит бифуркация потери симметрии и в системе существуют два несимметричных периодических решения (рис.5 - r=300 ), затем происходит каскад бифуркации удвоения (рис.4 - r=225).                                  Каждая из основных областей классической физики создала свою модель хаотической динамики: гидромеханика - уравнения Лоренца строительная механика - аттрактор Дуффинга-Холмса с двумя потенциальными ямами, электротехника - аттрактор Дуффинга-Уэды.       Еще одна простая модель возникла в динамике химических реакций, протекающих в некоторой смеси с перемешиванием. Предложил ее Ресслер:

dx/dt=-(y+z) dy/dt=x+a*y dz/dt=b+z*(x-c)

      Эти уравнения часто исследовались при a=b=0.2. Периодические движения с периодами 1,2 и 4 могут быть обнаружены при c=2.6; 3.5 и 4.1 соответственно (см. рис.1, 2, 3). При c > 4.23 могут встретиться хаотические движения (рис.4).          Модель Ресслера обладает свойствами линейного осциллятора с отрицательным коэффициентом затухания и обратной связью

 y''-a*y'+y=-z.

     Она служит примером многомерных систем, динамика которых допускает аппроксимацию одномерным отображением. Если провести сечение Пуанкаре при y=0 и построить на плоскости (x,z) одномерное отображение из точек Хn ,т.е. построить график зависимости Хn+1 от Xn , то обращает на себя внимание сходство полученной кривой с квадратичным, или логистическим, отображением. В модели Ресслера наблюдается удвоение периода.

Цепь Чуа - http://ru.Wikipedia.Org/wiki/%d0%a6%d0%b5%d0%bf%d1%8c_%d0%a7%d1%83%d0%b0

23. Классический геометрический подход к объяснению явления динамического хаоса. Гиперболическая теория. Отображение подковы Смейла, отображение Хенона, соленоид Смейла-Вильямса. Фракталы. Фрактальная размерность. Теория гомоклинического хаоса.

Подкова Смейла — предложенный Стивом Смейлом пример динамической системы, имеющей бесконечное число периодических точек (и хаотическую динамику), причём это свойство не разрушается при малых возмущениях системы.

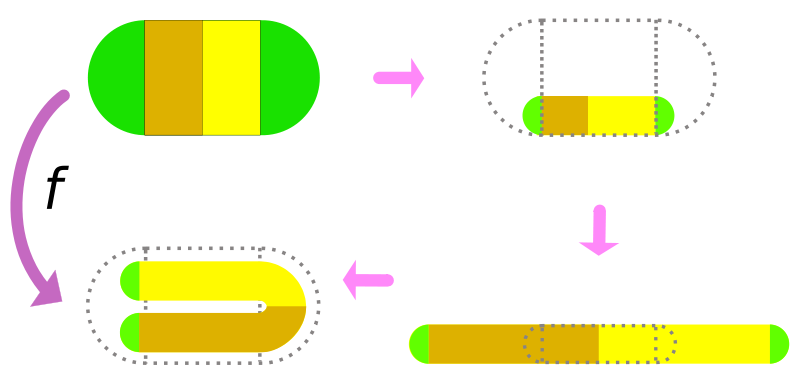
Соленоид Смейла — Вильямса — пример обратимой динамической системы, аналогичной по поведению траекторий отображению удвоения на окружности. Более точно, эта динамическая система определена на полнотории, и за одну её итерацию угловая координата удваивается; откуда автоматически возникает экспоненциальное разбегание траекторий и хаотичность динамики. Также соленоидом называют и максимальный аттрактор этой системы (откуда, собственно, и происходит название): он устроен как (несчётное) объединение «нитей», наматывающихся вдоль полнотория.

Определение

Отображением соленоида называют отображение

полнотория в себя, заданное как

Здесь диск для удобства рассматривается как единичный диск на комплексной плоскости: .

Максимальный аттрактор этого отображения (как и всю соответствующую динамическую систему) называют соленоидом Смейла — Вильямса.

Свойства

• Отображение соленоида гиперболично.

• Сам соленоид оказывается гомеоморфен множеству, получаемому при реализации процедуры надстройки над одометром — отображением прибавления единицы в 2-адических целых числах .

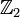• Динамика на соленоиде допускает символическое кодирование: точке соленоида можно (почти взаимно-однозначно) сопоставить двусторонне-бесконечным последовательностям нулей и единиц, причём применению отображения будет соответствовать левый сдвиг на пространстве последовательностей, а часть последовательности с положительными индексами будет являться двоичной записью угловой координаты.

Термин фрактал был предложен Бенуа Мандельбротом (B. Mandelbrot) в 1975 году для обозначения нерегулярных самоподобных математических структур. Основное определение фрактала, данное Мандельбротом, звучало так: "Фракталом называется структура, которая состоит из частей, которые в каком-то смысле подобны целому" [37]. Следует признать, что это определение, ввиду своей нестрогости, не всегда верно. Можно привести много примеров самоподобных объектов, не являющихся фракталами, например, сходящиеся к горизонту железнодорожные пути.

В самом простом случае небольшая часть фрактала содержит информацию обо всем фрактале. Строгое определение самоподобных множеств было дано Дж. Хатчинсоном (J. Hutchinson) в 1981 году. Он назвал множество самоподобным, если оно состоит из нескольких компонент, подобных всему этому множеству, т.е. компонент получаемых афинными преобразованиями - поворотом, сжатием и отражением исходного множества.

Однако самоподобие – это хотя и необходимое, но далеко не достаточное свойство фракталов. Ведь нельзя же, в самом деле, считать фракталом точку, или плоскость, расчерченную клетками. Главная особенность фрактальных объектов состоит в том, что для их описания недостаточно «стандартной» топологической размерности , которая, как известно, для линии равна 1 ( - линия одномерный объект), для поверхности , и т.д. Фракталам характерна геометрическая «изрезанность». Поэтому используется специальное понятие фрактальной размерности, введенное Ф. Хаусдорфом (F. Hausdorf) и А.С. Безиковичем. Применительно к идеальным объектам классической евклидовой геометрии она давала те же численные значения, что и топологическая размерность, однако новая размерность обладала более тонкой чувствительностью ко всякого рода несовершенствам реальных объектов, позволяя различать и индивидуализировать то, что прежде было безлико и неразличимо. Размерность Хаусдорфа - Безиковича как раз и позволяет измерять степень «изрезанности». Размерность фрактальных объектов не является целым числом, характерным для привычных геометрических. Вместе с тем, в большинстве случаев фракталы напоминают объекты, плотно занимающие реальное пространство, но не использующие его полностью.

Пусть есть множество в евклидовом пространстве размерности . Это множество покрывается кубиками размерности , при этом длина ребра любого кубика не превышает некоторого значения , т.е. .

Вводится зависящая от некоторого параметра и сумма по всем элементам покрытия:

.

Определим нижнюю грань данной суммы:

.

При уменьшении максимальной длины , если параметр будет достаточно велик, очевидно, будет выполняться:

При некотором достаточно малом значении параметра будет выполняться:

Промежуточное, критическое значение , для которого выполняется:

и называется размерностью Хаусдорфа-Безиковича (или фрактальной размерностью). Для простых геометрических объектов размерность Хаусдорфа-Безиковича совпадает с топологической (для отрезка =1, для квадрата =2, для куба =3 и т.д.)

Несмотря на то, что размерность Хаусдорфа-Безиковича с теоретической точки зрения определена безупречно, для реальных фрактальных объектов расчет этой размерности является весьма затруднительным. Поэтому вводится несколько упрощенный показатель - емкостная размерность . При определении этой размерности используются кубики с гранями одинакового размера. В этом случае, естественно, справедливо:

,

где - количество кубиков, покрывающего область . Путем логарифмирования и перехода к пределу при уменьшении грани кубика ( ) получаем:

если этот предел существует. Следует отметить, что в большинстве численных методов определения фрактальной размерности используется именно , при этом необходимо учитывать, что всегда справедливо условие: . Для регулярных самоподобных фракталов емкостная размерность и размерность Хаусдорфа-Безиковича совпадают, поэтому терминологически их часто не различают и говорят просто о фрактальной размерности объекта [13].

При проведении практических вычислений фрактальной размерности для реальных объектов используют следующий методический прием. Пусть на некотором этапе покрытия фрактала пришлось использовать кубиков с гранями размера , а на другом – элементов с гранями размера . Ввиду предполагаемой степенной зависимости справедливо:

,

откуда значение может оцениваться как:

.

24. Распределенная система уравнений рыночной экономики Магницкого.