Мультипликативная производственная функция

,

•  — выпуск продукции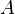

•  — многофакторная производительность труда (технический прогресс)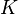

•  — объем используемого капитала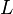

•  — затраты живого труда

Под техническим прогрессом в данной модели подразумевается вся совокупность качественных изменений труда и капитала. Таким образом, показатель технического прогресса является показателем времени. Технический прогресс называется нейтральным, так как он одинаково влияет на все задействованные для выпуска продукции ресурсы.

Условия модели

1. При отсутствии одного из факторов выпуск является нулевым.

2. Предельные продуктивности факторов являются положительными.

3. При увеличении объёмов ресурсов выпуск возрастает.

4. При увеличении объёмов ресурсов предельная производительность уменьшается.

5. При неограниченном увеличении одного из ресурсов выпуск также неограниченно увеличивается.

6. Норма сбережения капитала (инвестиции) является постоянной.

7. Норма выбывания капитала является постоянной.

8. Производственная функция обладает постоянной отдачей от масштаба (единичным эффектом масштаба).

11. Линейная динамическая система. Равенство спроса и предложения: динамическая модель Кейнса. Модель Самуэльсона-Хикса.

Модель Самуэльсона-Хикса включает в себя только рынок благ, и поэтому уровень цен и ставка процента предполагаются неизменными; объем предложения благ совершенно эластичен.

Объем потребления домашних хозяйств в текущем периоде зависит от величины их дохода в предшествующем периоде

C_t = C_a,t + C_yy_t-1,

где C_a - автономное потребление.

Предприниматели осуществляют автономные инвестиции, объем которых при заданной ставке процента фиксирован, и индуцированные инвестиции, зависящие от прироста совокупного спроса в предшествующем периоде

I_t = I_a,t +  (y_t-1 - y_t-2).

На рынке благ установится динамическое равновесие, если

,

(9.1)

где A_t = С_a,t + I_a,t.

Уравнение (9.1) является неоднородным конечно-разностным уравнением второго порядка, характеризующим динамику национального дохода во времени.

При фиксированной величине автономных расходов (A_t = A = const) в экономике достигается динамическое равновесие, когда объем национального дохода стабилизируется на определенном уровне , т.е. y_t = y_t-1 = y_t-2 = ... = y_t-n =  , где n - число периодов с неизменной величиной автономных расходов.

Из уравнения (9.1) следует, что  = A/(1 - C_y).

Посмотрим, какова будет динамика национального дохода, если в состоянии динамического равновесия изменится величина автономного спроса.

Освободимся от неоднородности в уравнении (9.1). Значения y_t и удовлетворяют равенству (9.1), поэтому можно записать следующее однородное конечно-разностное уравнение второй степени с постоянными коэффициентами:

,

(9.2)

где y_t   y_t -  .Так как y_t =   + y_t, то направление изменения y_t определяется направлением изменения y_t.

Из теории решения дифференциальных и конечно-разностных уравнений⁴ следует, что характер изменения y_t зависит от значения дискриминанта характеристического уравнения. Поскольку в данном случае дискриминант равен (C_y +  )² - 4 , то динамика национального дохода зависит от предельной склонности к потреблению, определяющей величины мультипликатора и акселератора.

Рис. 9.3. Четыре области сочетаний Cy,

Если (Cy +  )2 - 4  > 0, то изменение yt происходит монотонно; при (Cy +  )2 - 4  < 0 оно будет колебательным. Следовательно, график функции , изображенный на рис. 9.3, отделяет множество сочетаний Cy, , обеспечивающих монотонное изменение yt, от множества комбинаций из значений Cy, , приводящих к колебаниям yt.

Устремляется ли значение y_t к некоторой конечной величине или уходит в бесконечность, зависит от значения последнего слагаемого характеристического уравнения. Если  < 1, то равновесие установится на определенном уровне. При  > 1 нарушенное 1 раз равновесие больше не восстановится. Когда  = 1 , тогда значение yt будет колебаться с постоянной амплитудой.

В результате все множество сочетаний C_y и оказалось разделенным на пять областей, как это показано на рис. 9.3. Если значения C_y и указывают на область I, то после нарушения равновесия в результате изменения автономного спроса значение y_t монотонно устремится к новому равновесному уровню При значениях C_y и , находящихся в области II, национальный доход достигнет нового равновесного уровня, пройдя через затухающие колебания. Сочетания значений C_y и , расположенные справа от перпендикуляра, опущенного из точки B на ось абсцисс, соответствуют нестабильному равновесию. Когда сочетания значений C_y, указывают на область III, тогда динамика y_t приобретает характер взрывных колебаний. Комбинации значений C_y, в области IV приводят к тому, что после нарушения равновесия y_t монотонно устремляется в бесконечность. И наконец, если акселератор равен единице, то при любом значении предельной склонности к потреблению в случае нарушения равновесия возникают равномерные незатухающие колебания y_t.

12. Анализ и синтез динамических систем. Устойчивость динамических систем. Устойчивость и синергетика модели Самуэльсона-Хикса.

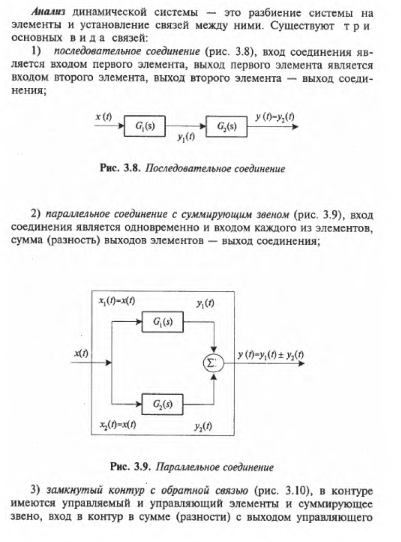
13. Линейные многосвязные динамические системы. Динамическая модель Леонтьева.

14. Нелинейные динамические системы. Управление динамическими системами.

15. Методы и модели анализа и прогнозирования рыночной конъюнктуры.

Рыночная конъюнктура – конкретная экономическая ситуация, сложившаяся на рынке в данный момент или ограниченный отрезок времени.

Конъюнктура характеризуется следующими факторами:

• степень сбалансированности рынка, т.е. соотношение между спросом и предложением;

• уровень устойчивости или колеблемости основных параметров;

• масштаб рыночных операций и степень деловой активности;

• уровень коммерческого риска;

• уровень конкуренции;

• положение рынка в определении точки сезонного или экономического цикла.

Существует несколько иное понятие рыночной конъюнктуры – это совокупность условий, определяющих рыночную ситуацию. Конъюнктура рынка имеет три принципиальные отличительные черты, обуславливающие использование соответствующего класса моделей:

• вариабельность;

• цикличность;

• динамичность.

Рынок подвержен колебаниям, случайным и не случайным, таким как, например, сезонным.

Система показателей конъюнктуры рынка:

1. Показатели, связанные с предложением товара:

   • объем предложения;

   • структура предложения;

   • динамика предложения;

   • эластичность предложения.

Модели и методы анализа и прогнозирования:

• динамика определяется с помощью выявления тренда, оценки колеблемости, оценки сезонности, индексных методов оценки динамики;

• структура методом группировок;

• эластичность 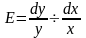показывает, на сколько процентов изменится y при изменении x на 1%, где процент означает относительное изменение. При анализе применяется классический математический анализ.