5. Математическая модель оптимальных управляемых процессов. Достаточные условия оптимальности.

Оптимальное управление — это задача проектирования системы, обеспечивающей для заданного объекта управления или процесса закон управления или управляющую последовательность воздействий, обеспечивающих максимум или минимум заданной совокупности критериев качества системы ^[1].

Для решения задачи оптимального управления строится математическая модель управляемого объекта или процесса, описывающая его поведение с течением времени под влиянием управляющих воздействий и собственного текущего состояния. Математическая модель для задачи оптимального управления включает в себя: формулировку цели управления, выраженную через критерий качества управления; определение дифференциальных или разностных уравнений, описывающих возможные способы движения объекта управления; определение ограничений на используемые ресурсы в виде уравнений или неравенств^[2].

Наиболее широко при проектировании систем управления применяются следующие методы: вариационное исчисление, принцип максимума Понтрягина и динамическое программирование Беллмана^[1].

Иногда (например, при управлении сложными объектами, такими как доменная печь в металлургии или при анализе экономической информации) в исходных данных и знаниях об управляемом объекте при постановке задачи оптимального управления содержится неопределённая или нечёткая информация, которая не может быть обработана традиционными количественными методами. В таких случаях можно использовать алгоритмы оптимального управления на основе математической теории нечётких множеств (Нечёткое управление). Используемые понятия и знания преобразуются в нечёткую форму, определяются нечёткие правила вывода принимаемых решений, затем производится обратное преобразование нечётких принятых решений в физические управляющие переменные.

Задача оптимального управления

Сформулируем задачу оптимального управления:

• Уравнения состояния: 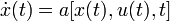(1).

• Граничные условия 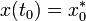, 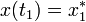(2).

• Минимизируемый функционал: .

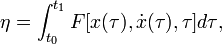здесь  — вектор состояния  — управление,  — начальный и конечный моменты времени.

Задача оптимального управления заключается в нахождении функций состояния и управления для времени , которые минимизируют функционал.

Метод динамического программирования

Метод динамического программирования основан на принципе оптимальности Беллмана, который формулируется следующим образом: оптимальная стратегия управления обладает тем свойством, что каково бы ни было начальное состояние и управление в начале процесса последующие управления должны составлять оптимальную стратегию управления относительно состояния, полученного после начальной стадии процесса^[6]. Более подробно метод динамического программирования изложен в книге^[7]

Достаточные условия оптимальности

Достаточные условия оптимальности управляемых процессов были предложены В. Ф. Кротовым, на основе которых были построены вычислительные алгоритмы последовательного улучшения, позволяющие находить глобальный оптимум в задачах управления

6. Задача Эйлера вариационного исчисления. Метод Лагранжа-Понтрягина для непрерывных управляемых процессов.

Вариационная задача означает, как правило, нахождение функции (в рамках вариационного исчисления — уравнения на функцию), удовлетворяющей условию стационарности некоторого заданного функционала, то есть такой функции, (бесконечно малые) возмущения которой не вызывают изменения функционала по крайней мере в первом порядке малости. Также вариационной задачей называют тесно связанную с этим задачу нахождения функции (уравнения на функцию), на которой данный функционал достигает локального экстремума (во многом эта задача сводится к первой, иногда практически полностью).

 Хотя задачи, к которым применимо вариационное исчисление, заметно шире, в приложениях они главным образом сводятся к двум основным задачам:

нахождение точек в пространстве функций, на котором определён функционал — точек стационарного функционала, стационарных функций, линий, траекторий, поверхностей и т. п., то есть нахождение для заданного Φ[f] таких f, для которых δΦ = 0 при любом (бесконечно малом) δf, или, иначе, где ,

нахождение локальных экстремумов функционала, то есть в первую очередь определение тех f, на которых Φ[f] принимает локально экстремальные значения — нахождение экстремалей (иногда также определение знака экстремума).

 Очевидно, обе задачи тесно связаны, и решение второй сводится (при должной гладкости функционала) к решению первой, а затем проверке, действительно ли достигается локальный экстремум (что делается независимо вручную, или — более систематически — исследованием вариационных производных второго и, если все они одного знака и хотя бы одна из них равна нулю, то производных более высокого порядка). В описанном процессе выясняется и тип экстремума. Нередко (например, когда функция стационарного функционала единственная, а все изменения функционала при любом большом возмущении имеют один и тот же знак) решение вопроса, экстремум ли это и какого он типа, заранее очевидно.

 Пусть задан функционал

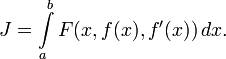
 с подинтегральной функцией , обладающей непрерывными первыми частными производными и называемой функцией Лагранжа или лагранжианом. Если этот функционал достигает экстремума на некоторой функции , то для неё должно выполняться обыкновенное дифференциальное уравнение

 которое называется уравнением Эйлера — Лагранжа.

7. Численные методы оптимизации для многошаговых процессов с непрерывным управлением.

8. Численные методы оптимизации для многошаговых процессов с дискретным управлением.

9. Динамическая модель оптимального развития многоотраслевой экономики.

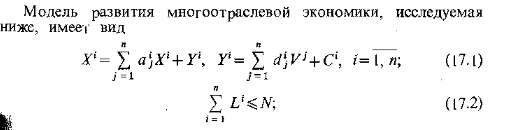
10. Экономика как нелинейная динамическая система. Модель Солоу.

Описанная модель развития и самоорганизации системы мировой экономики позволяет сделать следующие заключения о свойствах исследуемой системы.

В основе развития системы лежат два противоположно направленных процесса, являющихся ее изначально природным свойством: диссипация - рассеивание ресурсов и принцип минимума диссипации, который выражается оптимизацией распределения ресурсов для производства и благ для потребления на основе существующих договорных правил взаимодействия - институтов. Фактором, порождающим динамику, является рост численности населения в течение длительного времени. Природное свойство данной системы, выражающееся производством и неограниченным потреблением благ в условиях ограниченных ресурсов, предопределяет необходимость самостоятельного формирования ее структуры, которая бы обеспечивала эффективное распределение ресурсов для производства и благ для потребления, то есть самоорганизацию. Неравновесность системы также порождается этими двумя противоположными трендами.

Свойствами рассеивания и минимизации рассеивания ресурсов обладают все иерархические типы общественных систем: отдельно взятая страна, региональная, цивилизационная система и глобальная система - "мировая экономика". Наблюдается фрактальная симметрия основных свойств общественной системы "мировая экономика". Ее развитие происходит циклично с интервалом примерно в 70 лет. Каждый цикл развития проходит через конфликтный (50 лет) и бесконфликтный (20 лет) этапы, реализуемые бифуркационным и адаптационным механизмами развития, соответственно. На этапе действия бифуркационного механизма развития реструктуризуются старые и формируются новые связи системы, что сопровождается снижением количественного показателя развития. На этапе действия адаптационного механизма развитие проходит бесконфликтно и сопровождается скачкообразным ростом количественного показателя. Каждый цикл развития соответствует одному состоянию системы. Каждое последующее состояние системы обладает более сложной и более эффективной, с экономической точки зрения, структурой, чем предыдущее, что и обеспечивает целостность системы в условиях давления среды. Устойчивость имеет свои пределы, в которых происходит устойчивое развитие. Выход системы за пределы устойчивости вызывает крайне неравновесные состояния и неопределенность дальнейшего поведения системы, где одним из вероятных вариантов развития могут быть глобальный конфликт и самоуничтожение человечества.

Вот почему поддержание устойчивости системы "мировая экономика" является основным условием сохранения ее целостности. Расчет пределов устойчивости и определения условий поддержания системы в них является основной целью исследования поведения нелинейной динамической системы — развития глобальной цивилизации — на основе моделирования и проведения численного эксперимента.

Наблюдается усложнение структуры системы - самоорганизация как механизм реализации ее устойчивого развития.

Таким образом, можно сделать вывод, что система "мировая экономика" обладает рядом свойств, присущих нелинейной динамической системе: открытостью, неравновесностью, диссипативностью, а также свойством функционировать в двух различных режимах - бифуркационном и адаптационном, переходя из одного режима функционирования в другой в процессе развития, и свойством самоорганизации . Основная функция системы - развитие, посредством которого реализуется ее целеполагание - сохранение целостности.

Как уже отмечалось, основные свойства системы, порождающие развитие, - это процессы рассеивания ресурсов и минимизация рассеивания. Первый процесс проявляется в росте производства и потребления на основе повышения квалификации и численности населения, второй - в оптимизации распределения ресурсов для производства и благ для потребления в условиях ограниченности ресурсов и неограниченности потребления.

Целостность сохраняется благодаря поддержанию системы в границах устойчивого функционирования в процессе развития на основе существующей структуры системы, выраженной ее институтами.

Неоклассическая модель экономического роста Роберта Солоу основывается на производственной функции Кобба-Дугласа.

Основное отличие модели Солоу от производственной функции заключается в том, что автор вводит технический прогресс как фактор экономического роста наравне с такими факторами производства как труд и капитал. Модель описывает влияние трех вышеупомянутых факторов на экономический рост и описывается мультипликативной производственной функцией, составляющую основу модели, и рядом условий и ограничений.