Как интерпретировать полученное уравнение?

Т.к. коэффициент регрессии показывает как изменится результативный признак при росте одного признака-фактора на 1 ед. своего измерения при сохранении другого (или других) признака(-ов)-фактора(ов) на среднем уровне, имеем:

• Вывод 1: при росте коэффициента обновления основных средств на 1% (т.е. x₁ на ед. своего измерения), выработка продукции на 1 работника увеличивается в среднем на 2,051 млн.р. при сохранении удельного веса рабочих высокой квалификации на среднем уровне;

• Вывод 2: сформулируйте по аналогии сами.

Значимость параметров модели подтверждается или отклоняется при помощи t-критерия Стьюдента (пятый столбец таблице на рисунке 3.4). Выводы о значимости параметров модели сделайте сами.

!!!Подсказка!!!

Значимые параметры в программе Statistica автоматически выделяются красным цветом.

Ход выполнения задания 4: с помощью f-критерия оценить статистическую надежность уравнения регрессии и оценить r2. Разложить множественный коэффициент детерминации на частные

Рисунок 4.1. Описание регрессионной модели

Требуемые характеристики в программе расположены на белом поле над итоговой таблицей. На рисунке 4.1. оно выделено красной рамкой.

Так, R=0,8898 – это множественный коэффициент корреляции;

R?=0,792 – множественный коэффициент детерминации;

F(2,17)=32,306 – F-критерий Фишера (в скобках указаны число независимых переменных (2) и степень свободы (17)).

Множественный коэффициент вариации объясняет долю вариации результативного признака, вызванную вариацией признаков-факторов. Т.е. в нашем случае: 79,2% вариации выработки продукции на 1 работника объясняется вариацией коэффициента обновления основных средств и удельного веса рабочих высокой квалификации в общей численности рабочих.

Множественный коэффициент вариации можно разложить на частные (которые будут характеризовать вариацию результативного признака за счет вариации каждого признака-фактора):

или 67,6%;

или 11,6%.

и - коэффициенты парной корреляции, рассчитанные в пункте 2 (рисунок 2.3); β₁ и β₂ – бета-коэффициенты (первый столбец таблицы на рисунке 4.1).

Выводы для каждого из частных коэффициентов детерминации сделайте сами.

F-критерий Фишера подтверждает либо опровергает значимость и надежность построенной модели в целом. Т.е. если > - модель в целом значима.

для нашего случая, т.е. F(2;17) = 3,59. Вывод сформулируйте самостоятельно.

Ход выполнения задания 5: Рассчитать средние частные коэффициенты эластичности и дать на их основе оценку влияния факторов на результат

Частные коэффициенты эластичности рассчитываются по формуле:

,

где b_i – i-й коэффициент регрессии; - среднее значение i-го признака-фактора (т.е. x-а); - среднее значение результативного показателя.

Коэффициент эластичности показывает, на сколько процентов изменится результативный признак при увеличении признака-фактора на 1% от своего среднего уровня при сохранении другого (других) признака(ов)-фактора(ов) на среднем уровне.

Так,

;

.

• Вывод 1: При увеличении коэффициента обновления основных средств на 1% выработка продукции на 1 работника увеличивается в среднем на 0,931% при сохранении удельного веса рабочих высокой квалификации на среднем уровне;

• Вывод 2: Сформулируйте самостоятельно.

Ход выполнения задания 6: Рассчитать прогнозные значения y, если прогнозные значения факторов составят 80% от их максимальных значений. Доверительный интервал для прогноза рассчитать для уровней значимости 5% и 10%

Вначале необходимо рассчитать прогнозные значения факторов:

;

.

Далее в окне Multiple Regression Results переходим на третью вкладку Residuals/assumption/prediction:

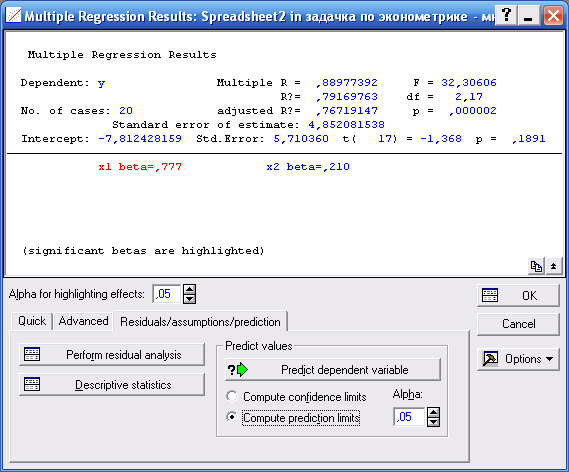
Рисунок 6.1. Расчет прогнозных значений y

И выставляем флажок Compute prediction limits, где можно менять уровень значимости для расчета интервала прогноза. В первом случае оставляем 0,05 (т.е. 5%).

Далее для того, чтобы задать прогнозные значения факторов, жмем кнопку Predict dependent variable и указываем рассчитанные ранее значения:

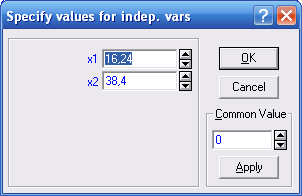
Рисунок 6.2. Указание прогнозных значений факторов

Далее жмем ОК и получаем результат:

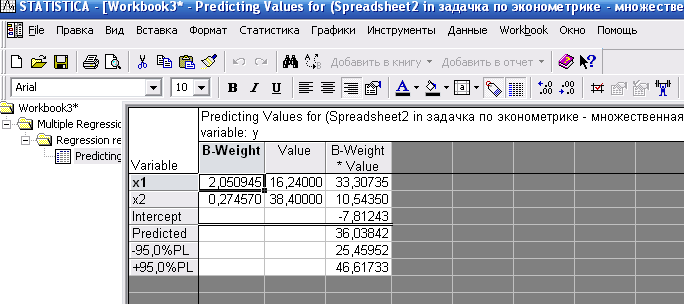
Рисунок 6.3. Прогнозные значения y для Alpha 5%

Точечный прогноз y при заданных значения факторов равен 36,04 млн. руб.; при уровне значимости 5% y (т.е. выработка продукции на 1 работника) будет заключен в пределах от 25,46 до 46,62 млн. руб.

Для выполнения второго задания возвращаемся в окно Multiple Regression Results, вкладка Residuals/assumption/prediction и указываем уровень значимости Alpha 0,1 (т.е. 10%):

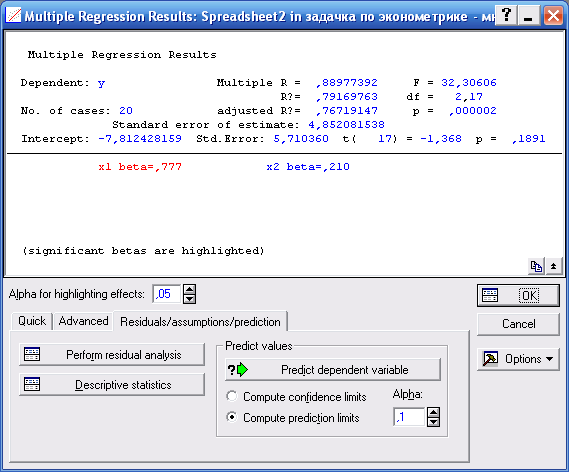
Рисунок 6.4. Расчет прогнозных значений у при уровне значимости 10%

Заново задаем прогнозные значения факторов (рисунок 6.2) и жмем ОК, получаем результат:

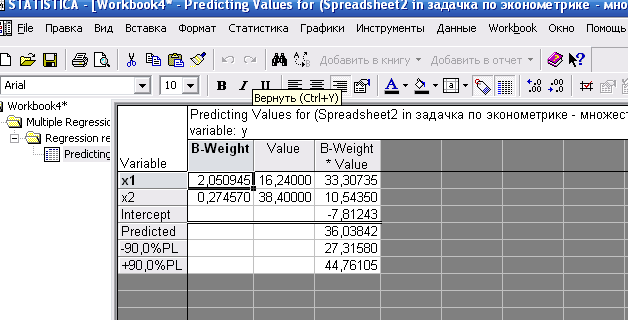
Рисунок 6.5. Прогнозные значения y для Alpha 10%

Значение точечного прогноза не изменяется, меняются границы интервала прогноза. Сделайте вывод, в каких пределах заключен y при уровне значимости 10%.