Лабораторна робота № 5 вимірювання питомого опору матеріалів електронної техніки чотиризондовим методом

Мета роботи: Визначення питомого опору напівпровідників чотиризондовим методом вимірювання

1 Теоретичні відомості

Чотиризондовий метод вимірювання питомого опору напівпровідників є найпоширенішим. Крім високих метрологічних показників перевага четиризондового методу полягає в тому, що для його застосування не потрібне створення омічних контактів до зразка, можливе вимірювання питомого опору об'ємних зразків найрізноманітнішої форми і розмірів, а також питомого опору шарів напівпровідникових структур. Умовою для його застосування з погляду форми зразка є наявність плоскої поверхні, лінійні розміри якої перевершують лінійні розміри системи зондів.

Теорія методу. Розглянемо теоретичні основи чотиризондового методу вимірювання питомого опору стосовно до зразка, що представляє собою напівнескінченний об’єм, обмежений плоскою поверхнею.

На плоскій поверхні зразка уздовж прямої лінії розміщені чотири металевих зонди з малою площею зіткнення (рис.1), відстані між якими , , . Через два зовнішніх зонди 1 і 4 пропускають електричний струм , на двох внутрішніх зондах 2 і 3 вимірюють різницю потенціалів . За вимірюваним значенням різниці потенціалів між зондами 2 і 3 і струму, що протікає через зонди 1 і 4, можна визначити питомий опір зразка.

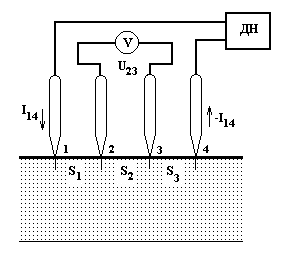
Рисунок 1 - Електрична схема вимірювання питомого опору чотиризондовим методом: ДН – джерело постійної напруги; V – вольтметр

Щоб знайти аналітичний зв'язок між питомим опором , струмом , і напругою , необхідно спочатку вирішити більш просту задачу, зв'язану з протіканням струму через окремий точковий зонд, що знаходиться в контакті з плоскою поверхнею напівпровідникового зразка напівнескінченного об’єму (рис.2).

Рисунок 2 - Модель зонда

Оскільки просторовий розподіл електричного потенціалу в зразку має сферичну симетрію, то для його визначення досить вирішити рівняння Лапласа в сферичній системі координат, у якому залишений лише член, що залежить від ,

,

за умови, що потенціал у точці позитивний і прагне до нуля при дуже великих . Інтегрування цього рівняння з врахуванням зазначених граничних умов дозволяє одержати рішення:

.

Константу інтегрування можна обчислити з умови для напруженості електричного полючи при деякім значенні :

.

Оскільки щільність струму, що протікає через півсферу радіусом , , а відповідно до закону Ома , то . Остаточно одержимо:

. (1)

Очевидно, що розподіл потенціалу буде таким же, коли форма контакту зонда з поверхнею зразка має вигляд півсфери кінцевого діаметра.

Нехай радіус контакту дорівнює . Тоді електрична напруга зразка дорівнює електричному потенціалу зонда:

. (2)

З порівняння напруги на приконтактному шарі товщиною

,

і напруги на зразку (2) випливає, що основна зміна потенціалу відбувається поблизу зонда. Наприклад, при напруга на зразку перевершує напругу на шарі товщиною усього лише на 10%. Це означає, що значення струму, що протікає через зонд, визначається головним чином опором приконтактної області, довжина якої чим менше, чим менше радіус контакту.

Лінійне розташування зондів. Сформулюємо припущення, на яких заснований чотиризондовий метод вимірювання питомого опору: 1) зонди розташовані на плоскій поверхні однорідного ізотропного зразка напівнескінченного об’єму; 2) зонди мають контакти з поверхнею зразка в точках, що розташовані уздовж прямої лінії; 3) інжекція носіїв заряду в об’ємі зразка відсутня.

За принципом суперпозиції електричний потенціал у будь-якій точці зразка дорівнює сумі потенціалів, створюваних у цій точці струмом кожного зонда. При цьому потенціал має позитивний знак для струму, що втікає в зразок (зонд 1), і негативний знак для струму, що витікає зі зразка (зонд 4). Для системи зондів, відстані між який , , , потенціали вимірювальних зондів 2 і 3 набувають значення:

,

.