Характеристики векторного поля.
Рассмотрим поле
вектора
,
.
Векторной линией данного векторного поля называется линия, касательная к которой в любой точке параллельна вектору поля, определенному в этой точке. Примеры: в случае поля скоростей векторные линии называются линиями тока, в случае электростатического поля – силовыми линиями.
Характеристика векторного поля:
Дивергенцией
данного
векторного поля с непрерывно
дифференцируемыми компонентами
является скалярная величина
.
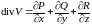Термин дивергенция (или расхождение) поля в точке связан с наличием дополнительных источников или стоков в этой точке. Если значение дивергенции в точке больше нуля, то в этой точке находится источник, а если меньше нуля – сток. Если во всех точках поля дивергенция равна нулю, то это поле называется соленоидальным.
Циркуляцией вектора , , вдоль некоторой замкнутой ориентированной кривой C , находящейся внутри множества , назовем следующий криволинейный интеграл второго рода:
.
Ротором вектора поля с непрерывно дифференцируемыми компонентами назовем следующую векторную величину:
.
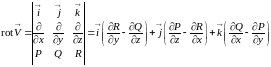Здесь «умножение» элементов второй строки на элементы третьей строки означает, что от функции из третьей строки берется соответствующая производная.
Ротор иногда называют вихрем, он характеризует вращение поля в данной точке. Если во всех точках векторного поля ротор равен нулю, то поле называется потенциальным. Если во всех точках векторного поля дивергенция и ротор равны нулю, то такое поле называется гармоническим.
Для потенциального
поля
,
существует
скалярная функция
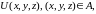такая, что
или
.
При этом функция
называется потенциалом вектора
.
Действительно, если такая функция
существует,
то
.
Разложение произвольного векторного поля.
Пусть , , – произвольное векторное поле. Покажем, что вектор может быть представлен как сумма двух векторов, один из которых представляет потенциальное, а другой – соленоидальное векторное поле.
Пусть вектор
.
Какой должна быть эта функция
,
чтобы вектор
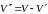был соленоидальным?
Поскольку
,
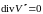получим
,
то есть
.
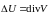Таким образом, чтобы разложить исходный
вектор
на сумму потенциального и соленоидального
векторов, необходимо сначала решить
уравнение Пуассона
.
Такое уравнение всегда имеет решение
(и даже бесчисленное множество решений).
Определив
,
мы получим потенциальный вектор
.
Теперь по построению вектор
соленоидальный. Следовательно, требуемое
разложение
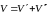построено.
Оператор Гамильтона (набла-оператор).
Для упрощения
записи характеристик скалярных и
векторных полей был введен символический
векторный оператор, имеющий вид
.
Символическое «умножение» этого
оператора на какую-то величину означает,
что каждая из компонент
оператора
применяется к этой величине.
Например, если – скалярная величина, то
.
Для векторных
величин возможно как скалярное, так и
векторное умножение. Проследим, что
дадут такие произведения с
оператором
в случае векторного поля
.
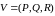Скалярное
произведение:
.
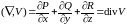Векторное
произведение:
.
Отдельный интерес представляет определенный для скалярных полей оператор
.
Такой оператор
называется оператором Лапласа. Функции,
удовлетворяющие уравнению Лапласа
называются гармоническими
в
функциями.