Связь между криволинейным интегралом второго рода вдоль замкнутой кривой на плоскости и двойным интегралом. Формула Грина.
Пусть C
– кусочно-гладкая замкнутая кривая,
ограничивающая область D.
На кривой C
задано такое направление, что при
движении в этом направлении область D
остается слева. Функции
и
непрерывны в области D
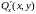вплоть до ее границы, кроме того, функции
и
также непрерывны в D
вплоть до границы. Тогда справедлива
формула Грина
.
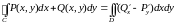Условие независимости криволинейного интеграла второго рода от пути интегрирования на плоскости.
В общем случае
криволинейный интеграл
,
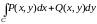где кривая C
соединяет точки A
и B
на плоскости XY,
зависит от пути C.
Зададимся вопросом, каким условиям
должны удовлетворять функции
и
в области
,
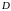чтобы результат интегрирования по
любой кривой, лежащей внутри
,
и соединяющей две фиксированные точки,
был одинаковым.
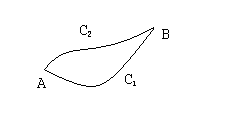
Очевидно, что
условие независимости результата
интегрирования криволинейного интеграла
по кривой, соединяющей две фиксированные
точки области, от формы этой кривой
равносильно условию равенства нулю
интеграла по любой замкнутой кривой,
лежащей в этой области. Действительно,
обозначим через
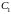и
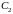две кривые, лежащие в
,
с общими начальной и конечной точками.
Тогда кривая
,
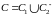где знак «-» означает, что соответствующая
кривая проходится в противоположном
направлении, будет замкнутой.
Следовательно, соотношение
равносильно тому,
что
.
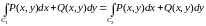Необходимым и
достаточным условием того, что
,
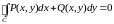где
– любая замкнутая кривая, лежащая в
области
,
является равенство
,
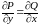выполняющееся всюду в
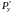для непрерывных функций
и
.
Для доказательства этого факта
используется формула Грина.
Заметим, что
выполнение условие
– это условие того, что подынтегральное
выражение
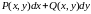является полным дифференциалом некоторой
функции
,
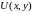называемой потенциалом. Действительно,
если
и
,
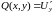то
.
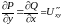Таким образом,
выполнение условие
обеспечивает представление
,
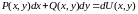и криволинейный интеграл от этого
выражения по любой кривой, соединяющей
две фиксированные точки A
и B
с координатами
,
соответственно, равен
.
Поверхностные интегралы Поверхностный интеграл первого рода.
Основной задачей, приводящей к поверхностному интегралу первого рода, является задача о вычислении массы неоднородной оболочки.
Пусть S
– поверхность в пространстве XYZ.
Тяжелая неоднородная оболочка расположена
в пространстве в виде этой поверхности.
Плотность оболочки, рассчитанная на
единицу площади поверхности, зависит
от местоположения точки на поверхности
и равна
,
причем
–
непрерывная на S
функция. Для того, чтобы вычислить
массу неоднородной оболочки, разобьем
поверхность S
на n
фрагментов
с площадями
и на каждом таком фрагменте
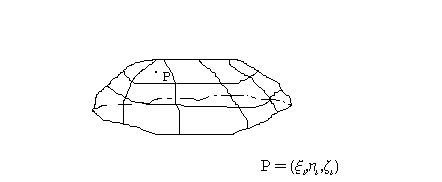
выберем точку
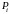с координатами
.
Найдем значение
.
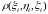Предполагая, что площадь i-го
поверхностного фрагмента мала и учитывая,
что плотность непрерывна, получим, что
масса этого фрагмента будет приблизительно
равна
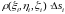, причем чем меньше фрагмент, тем точнее
полученная масса этого фрагмента.
Поэтому массу всей оболочки можно
получить, просуммировав массы всех
фрагментов и устремив к нулю площади
фрагментов, одновременно увеличивая
количество фрагментов, на которые
разбита поверхность. Таким образом,
выражение для массы оболочки будет
иметь вид
.
Представим предел
интегральной суммы через двойной
интеграл, так как сомножитель
– элемент площади. В результате
предельного перехода получим
.
Интеграл, стоящий в правой части последнего выражения, называется поверхностным интегралом первого рода или поверхностным интегралом по площади поверхности. Заметим, что результат интегрирования не зависит от выбора стороны оболочки.
С помощью поверхностного интеграла 1-го рода можно вычислять не только массу оболочки, но и другие физические характеристики оболочки: моменты, центр тяжести….