Лабораторная работа № 5 определение главных напряжений при совместном действии изгиба и кручения
Цель работы: экспериментальное определение величины главных напряжений в тонкостенной трубе при совместном действии изгиба и кручения; сравнение полученных величин с вычисленными теоретически.
1. Постановка опыта
Опыт проводится на специальной установке типа СМ18. Схема установки приведена на рис. 10 а. Трубу 1, изготовленную из алюминиевого сплава Д16Т, жёстко закреплённую на одном конце, нагружают на свободном конце двумя грузами РЛ и РП разной величины. Грузы приложены на расстояниях a от оси трубы и создают изгибающие крутящие моменты в поперечных сечениях. При этом в поверхностном слое трубы возникает плоское напряженное состояние, потому что внешняя поверхность трубы свободна от напряжений и одно из трёх главных напряжений (перпендикулярное к внешней поверхности) равно нулю. Напряженное состояние в некоторой верхней точке К сечения, расположенного на расстоянии l от свободного конца трубы, изображено на рис. 10, б.
Направление
главных напряжений заранее неизвестно
и зависит от соотношения
и
(крутящего и изгибающего моментов).
Очевидно,
что для определения трёх неизвестных:
двух главных напряжений
и
(или
)
и угла, определяющего направление
первого главного напряжения (первой
главной площадки) - необходимо получить
из опыта три какие-либо деформации.
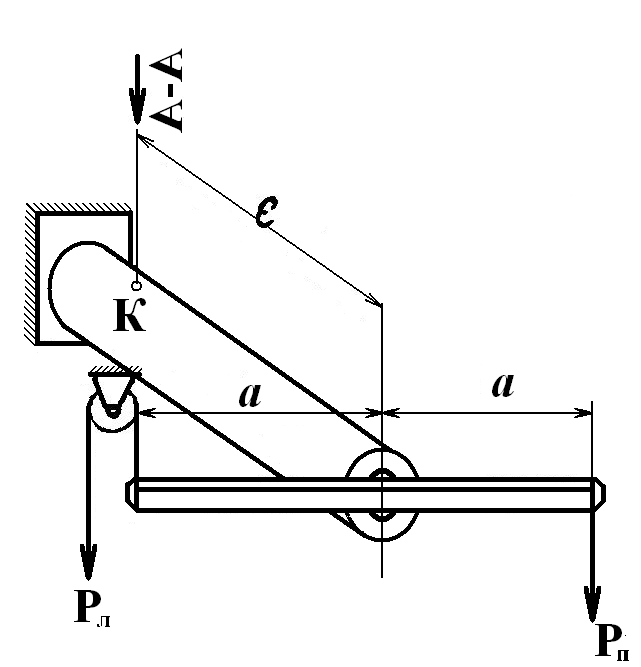
а
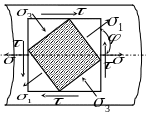
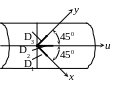
б Вид по А-А
в
Рис.10
Обычно в данной точке измеряют три линейных деформации εx, εy в направлениях некоторых взаимно перпендикулярных осей X и У и под углом 45° к ним εu. Для этого в исследуемой точке К приклеивают три тензорезистора так, как показано на рис. 10, в. Такая комбинация тензорезисторов называется прямоугольной розеткой. Получим расчётные формулы для прямоугольной розетки.
В соответствии с обобщённым законом Гука деформация в направлении X при плоском напряженном состоянии
(5.1)
Для плоского напряженного состояния известна формула для определения напряжений σх на площадке, расположенной под углом α. К первой главной площадке, через главные напряжения определяются σx и σу
(5.2)
Напряжение
определяется из формулы (5.2) после
подстановки вместо
угла 90° +
:
(5.3)
Подставим значения σх в формулу (5.1), тогда
(5.4)
Запишем обобщенный закон Гука для плоского напряженного состояния в главных напряжениях
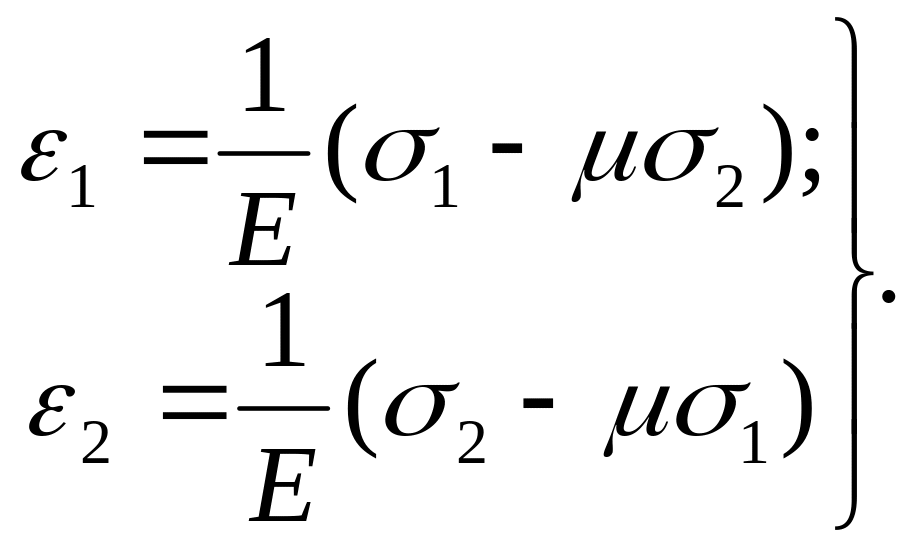(5.5)
Подставляя в формулу (5.5) в (5.4), имеем:
(5.6)
После подстановки известных из тригонометрии равенств
и
(5.6) примет вид
(5.7)
Чтобы
получить аналитические формулы для
и
,
достаточно в выражение (5.7) вместо
подставить соответственно углы 90°+
;
45°+
.
С учётом того, что cos2(90°+ ) = - cos2 и cos2(45°+ ) = - sin2 , получим
(5.8)
(5.9)
Для
разрешения последних трёх уравнений
относительно
,
и
сложим почленно (5.7) и (5.3). Получим:
(5.10)
Подставим в выражение (5.10) в формулу (5.9) и (5.7):
(5.11)
Возведём оба равенства (5.11) в квадрат, сложим и извлечём корни из обеих частей полученного уравнения:
(5.12)
Складывая
и вычитая уравнения (5.12) и (5.10), одновременно
раскрывая скобки и группируя слагаемые
под корнем, приходим к формуле для
вычисления главных деформаций через
деформации
,
и
,
определяемые с помощью тензорезисторов
Т1,
Т2,
Т3:
(5.13)
После
вычисления главных деформаций определяем
из обобщенного закона Гука (после
разрешения формул (5.5) относительно
и
)
главные напряжения:
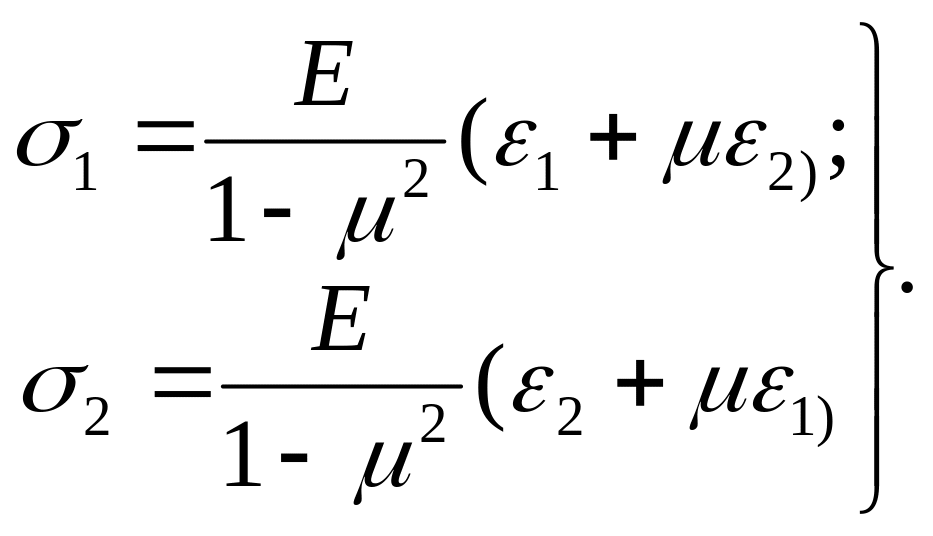(5.14)
Заметим,
если вычисленные главные напряжения
имеют разные знаки, то это будут
и
,
а
= 0, так как индексация главных напряжений
ведётся с учётом неравенства
.
Разделив первое уравнение (5.11) на второе, получим формулу для вычисления угла α, определяющего положение главных площадок:
(5.15)
Так
как tg2α
– периодическая функция с периодом
,
то уравнению (5.15)
будут удовлетворять углы
и
,
определяющие положение первой и второй
главных площадок.