2. Теоретический расчёт исследуемых величин

Для теоретического определения исследуемых величин раскроем сначала статическую неопределимость рамы.

Замкнутая кольцевая рама три раза статически неопределима, но условия симметрии позволяют сократить число неизвестных до одного.

Мысленно рассечём раму по горизонтальной оси симметрии СК, получаем эквивалентную систему в виде, изображенном на рис. 5,а (верхняя часть). Из условий симметрии относительно вертикальной оси – линии действия внешней силы Р – вытекает, что

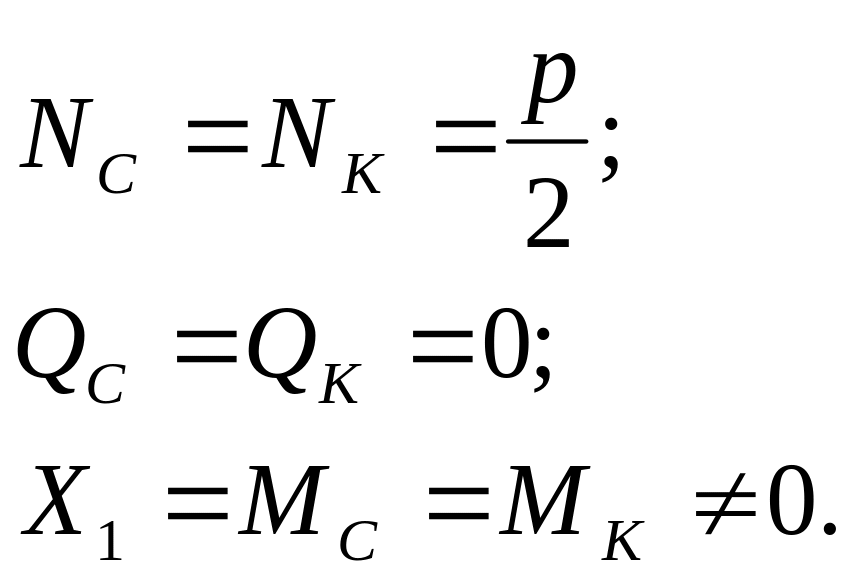
Для определения Х₁ воспользуемся каноническим уравнением метода

сил:

(2.1)

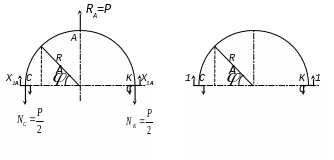
Рис. 5 Рис. 5

Величины Δ_1Р и вычислим с помощью интеграла Мора. В сечении, определяемом угловой координатой , изгибающий момент (для четверти окружности)

По условиям симметрии аналогично находится момент для других четвертей.

Момент от единичного силового фактора (рис. 5,б) m = - 1. Тогда с учётом того, что dS = R·d , имеем

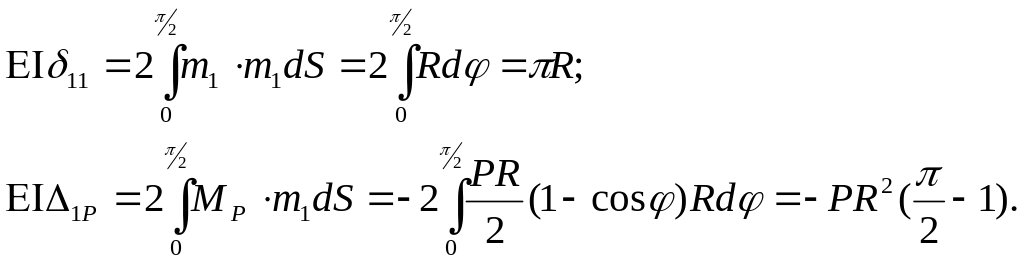
Из уравнения (2.1) следует, что

Изгибающий момент в произвольном сечении четверти рамы равен сумме момента от заданных сил М_Р и момента m₁ (с учётом знака), увеличенного в Х₁ раз, т.е.

(2.2)

Поскольку статическая неопределимость рамы раскрыта, так как известно выражение (2.2) момента в основной системе, то для определения уменьшения диаметра СК достаточно рассечь кольцо в любом сечении, например в сечении Д, и в точках С и К приложить противоположно направленные единичные силы (рис. 6).

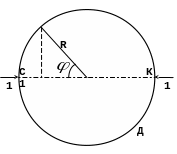
Рис. 6

Тогда

;

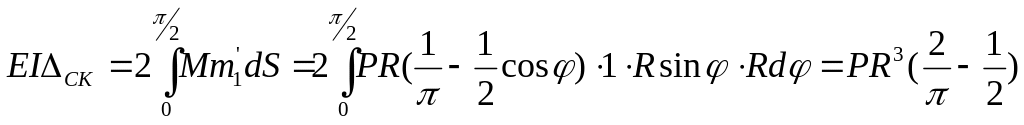(2.3)

Выражение для теоретического определения увеличения диаметра Δ_АВ в вертикальном направлении получить самостоятельно.

3. Порядок выполнения работы

Индикаторы устанавливают таким образом, чтобы обеспечить измерения перемещений в возможном интервале их изменения (5-6 мм). Нагрузив раму весом подвески, стрелки индикаторов устанавливают на нулевую отметку. Затем последовательно нагружают кольцевую раму, каждый раз снимая показания индикаторов. Нагрузку увеличивают равными ступенями (5 Н). Результаты измерений заносят в табл. 2.

Средние приращения показаний индикаторов с учётом цены их деления (0,01 мм) определяют исследуемые в опыте величины (перемещения на ступень нагрузки):

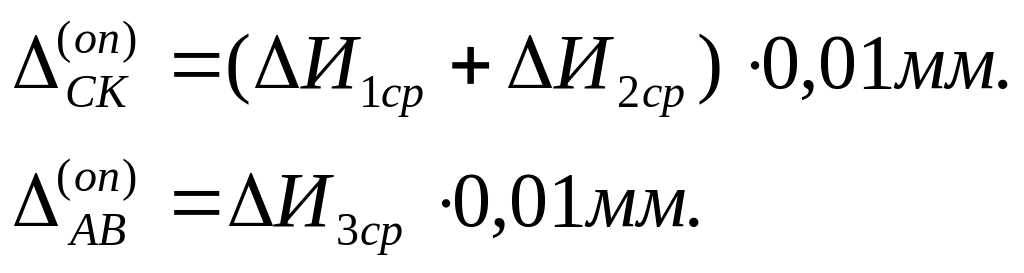
Таблица 2

Нагрузка Р, Н	Показания индикаторов			Приращение нагрузки ΔР, Н	Приращение показаний индикаторов
	И1	И2	И3		ΔИ1	ΔИ2	ΔИ3
Средние значения				ΔРср =	ΔИ1ср =	ΔИ2ср =	ΔИ3ср =

Производят определение этих же величин теоретическим расчётом: Δ_ск^(теор) определяют по формуле (2.3), а Δ_АВ^(теор) – по выведенной самостоятельно формуле. Определяют процент расхождения между опытным и теоретичес- кими значениями исследуемых величин.