3. Обработка результатов работы и подготовка отчета по работе

По данным табл.6. подсчитывают средние значения приращений отсчётов для каждого тензорезистора и вычисляют напряжения в соответствующих точках по формуле закона Гука

где ε₀ – цена деления измерительной шкалы электротензометра;

Е – модуль продольной упругости материала образца,

Е = 2 · 10⁵ МПа (2 · 10⁶ кгс/см²).

По полученным данным построить эпюры распределения нормальных напряжений в образце для сечений АВ и СД.

Теоретический коэффициент концентрации напряжений определяется отношением наибольшего местного напряжения в ослабленном сечении к номинальному для этого сечения:

где ;

Здесь ΔР – величина приращения растягивающей силы на ступень нагружения;

F_нетто – площадь ослабленного сечения.

В отчёт включить: схему образца с указанием места наклейки тензорезисторов и их номера, размеры поперечного сечения образца, таблицу записи результатов испытания, вычисления и эпюры напряжений.

Для защиты (допуска) лабораторной работы необходимо подготовить ответы на нижеприведенные контрольные вопросы.

Контрольные вопросы

1. Когда возникает концентрация напряжений?

2. Какие напряжения называются местными?

3. Какие напряжения называются номинальными и как они определяются для различных случаев нагружения образца: растяжения, изгиба, кручения?

4. Что представляет собой теоретический коэффициент концентрации напряжений?

5. Что называется эффективным коэффициентом концентрации напряжений?

6. Какие меры применяются для уменьшения концентрации напряжений?

7. Почему концентрация напряжений менее опасна для пластических материалов, чем для хрупких?

8. Почему концентрация напряжений не опасна для чугуна?

9. С помощью каких приборов происходит определение деформаций?

10. Каким образом можно вычислить нормальные напряжения по измеренной относительной деформации?

11. На чём основано применение тензорезисторов для измерения деформаций?

12. В чём преимущество тензорезисторов по сравнению с другими видами тензометров?

13. Какие размеры образца должны быть измерены?

14. Как определяется величина наибольшего местного напряжения?

Лабораторная работа № 7 исследование напряжений в плоском кривом брусе большей кривизны при изгибе

Цель работы: проверка опытным путём закона распределения нормальных напряжений в сечении кривого бруса при изгибе.

1. Постановка опыта

Работа проводится на универсальной машине типа Р-20. Для испытания используется кривой брус с прямоугольным поперечным сечением (рис. 12).

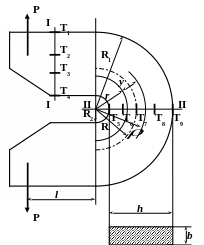
Рис. 12

При растяжении кривого бруса силой Р, приложенной вдоль вертикальной оси, в опасном сечении II-II возникают продольная сила N = P и изгибающий момент M = P(R+l). Нормальные напряжения в сечении кривого бруса изменяются по гиперболическому закону

,

где F = b·h – площадь поперечного сечения;

S = F·(R-r) – статический момент площади сечения относительно

нейтральной оси;

y – расстояние от нейтральной оси до рассматриваемого

волокна;

– радиус рассматриваемого волокна (расстояние от

центра кривизны бруса);

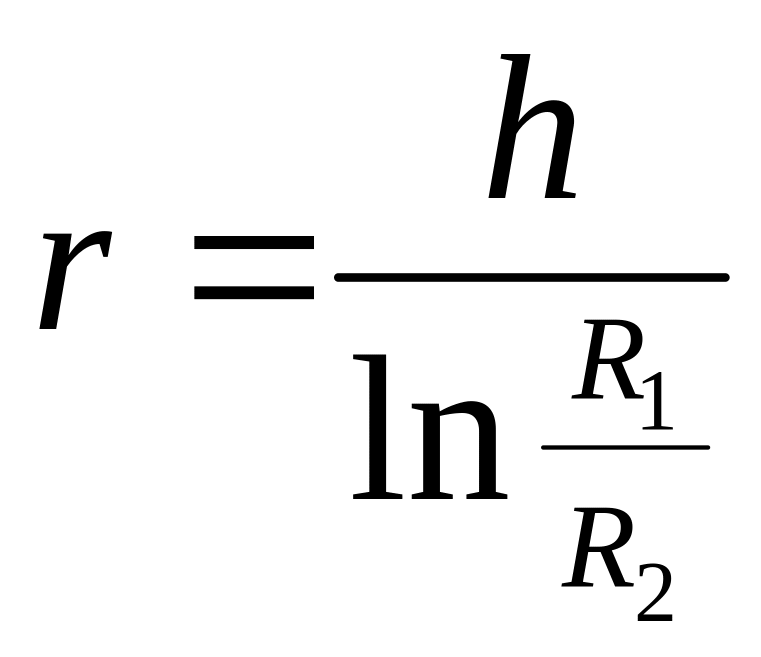– радиус нейтрального слоя при чистом изгибе;

– радиус центральной оси бруса;

R₂ и R₁ – внутренний и наружный радиусы бруса.

В сечении I-I исследуется распределение нормальных напряжений при плоском изгибе прямого бруса (выполняется по указанию преподавателя).

Для выяснения закона распределения нормальных напряжений кривого бруса в 5-ти точках боковой поверхности его опасного сечения II-II (и в четырёх точках сечения I-I) предварительно наклеены электрические датчики сопротивления (тензорезисторы).

Для замера деформаций тензорезисторы подключают к электротензометру. Вследствие нагружения внутренние волокна бруса растягиваются, а наружные- сжимаются. Вместе с волокнами изменяется длина проволоки тензорезисторов, их электросопротивление, что и фиксируется измерительным прибором.