5.3 Понятие и виды структурных средних величин

Степенные средние достаточно достоверно отражают сущность явления при нормальном (или близком к нему) распределении признака в статистической совокупности. Однако в социально-экономических явлениях такой вид распределения встречается редко. В асимметричном распределении более верное представление о типичной величине признака позволяют получить структурные средние величины.

К ним относят медиану, квартили, квинтили, децили, перцентили и т.д. Большинство авторов структурной средней величиной считают и моду, но, строго говоря, она не отражает структуру статистической совокупности.

5.4 Мода и ее определение в дискретном и интервальном вариационном ряду распределения

Мода (Мо) — это наиболее часто встречающееся значение признака в статистической совокупности или значение варианты с наибольшей частотой. В дискретных и интервальных рядах моду рассчитывают по разному.

В дискретных вариационных рядах мода – это признак, которому соответствует наибольшая частота.

В зависимости от того, равны интервалы между собой или нет, применяют тот или иной подход к определению моды. Для определения моды в интервальных вариационных рядах с равными интервалами сначала по наибольшей частоте находят модальный интервал, затем рассчитывают моду по формуле:

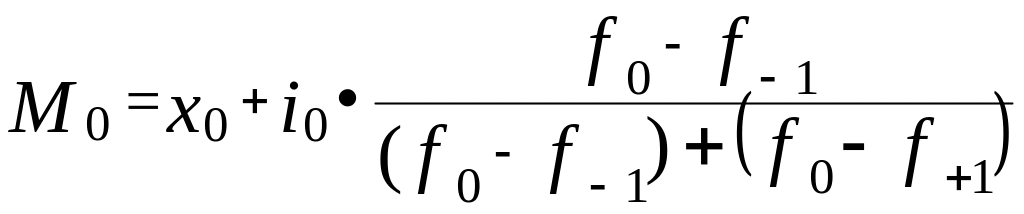, (5.18)

где – начало модального интервала,

– длина модального интервала,

– частоты интервалов, стоящих перед модальным, модального и после модального.

Если интервалы вариационного ряда не равны между собой, то для определения моды необходимо проделать следующие действия:

1) для каждого интервала на основе частот и длин интервалов

лов рассчитать величину, которая называется абсолютной плотностью распределения, как отношение частоты к длине интервала;

2) по наибольшей абсолютной плотности распределения найти модальный интервал;

3) определить значение моды по вышеприведенной формуле, подставив вместо частот абсолютные плотности распределения.

Модальное значение признака можно найти по графику.

Вариационный ряд может содержать несколько мод. Вариационный ряд, имеющий одну моду, называется унимодальным, две - бимодальным, три и более - мультимодальным.

5.3 Структурные средние в дискретном и вариационном ряду распределения

Для получения более полной характеристики вариационного ряда помимо средней величины и моды рассчитываются так называемые структурные показатели. К ним относятся медиана, квартили, децили и перцентили (персентили).

Медианой (Me) является значение варианты, находящейся в центре упорядоченной по возрастанию значений признака совокупности. Медиана делит вариационный ряд на две равные части. При этом 50% единиц совокупности имеют значение меньше медианного, а 50% - больше медианного.

В дискретном ряду распределения медиана находится по номеру. Номер медианы находится по формуле:

, (5.19)

где n – число единиц в совокупности.

При четном количестве единиц в совокупности медиана получается путем расчета средней арифметической из двух рядом стоящих значений признаков.

В интервальном ряду распределения медиана рассчитывается по формуле:

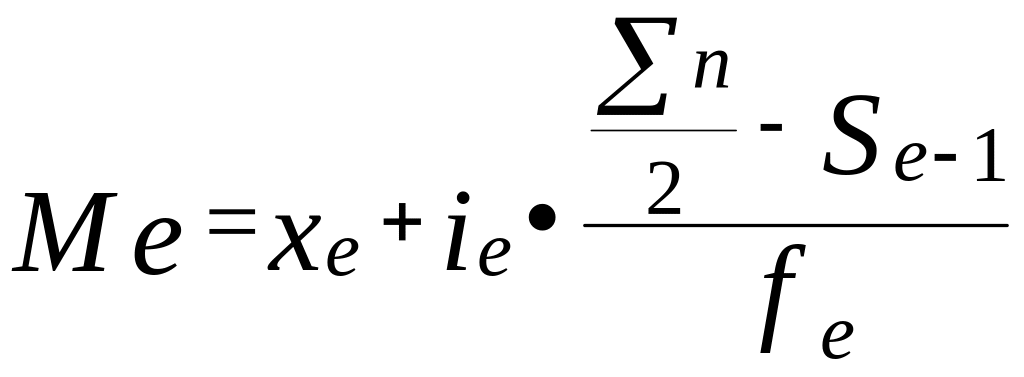, (5.20)

где - начало медианного интервала,

– длина медианного интервала,

– сумма накопленных частот до интервала, в котором находится медиана,

– частота медианного интервала.

Медиана имеет свойство, благодаря которому используется в экономических и коммерческих расчетах:

(5.21)

В нормальных рядах распределения мода и медиана совпадают со средним арифметическим значением.

Лекция 6 Ряды динамики

6.1 Понятие и виды рядов динамики

6.2 Показатели рядов динамики