Уточнені дані нормалізованих критеріїв за альтернативними інноваційними проектами

Номер варіанту (J=1)	Безрозмірні величини критеріїв оптимальності
1	0	0,25	0,75
2	0,1538	0,75	0,875
3	0,2308	1	1
4	0,6154	0,375	0
5	0,8462	0	0,625
6	1	0,125	0,5

Формула для розрахунку за методом справедливого компромісу має вигляд [16, с.361]:

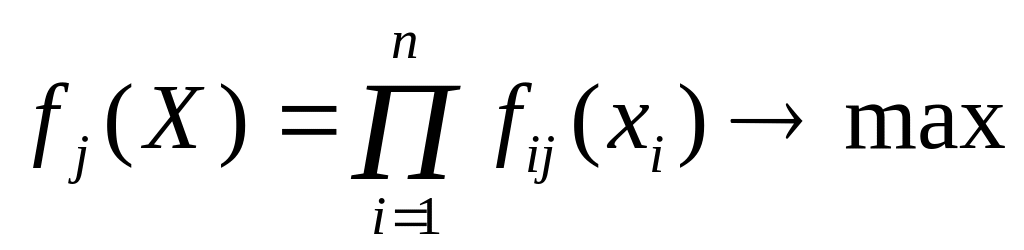. (7)

Тобто необхідно знайти добуток безрозмірних нормалізованих величин критерії оптимальності проектів, які наведені в таблиці 6.

Таблиця 6.

Номер варіанту J=1	Безрозмірні величини критеріїв оптимальності			Добуток безрозмірних величин критеріїв оптимальності
1	0	0,25	0,75	0
2	0,1538	0,75	0,875	0,1009
3	0,2308	1	1	0,2308
4	0,6154	0,375	0	0
5	0,8462	0	0,625	0
6	1	0,125	0,5	0,0625

Відповідь: з наведених в таблиці 6 розрахунків видно, що економічно найбільш ефективним за методом справедливого компромісу є третій варіант з альтернативних інноваційних проектів.

Задача 11. Виберіть з наведених в таблиці 1 один найбільш ефективний інноваційний проект, використовуючи метод, що заснований на визначенні сумарного за всіма критеріями відхилення від ідеальної точки (дивіться умови задачі 9).

Згідно інформації, наведеної в таблиці 5, визначимо ідеальні (оптимальні) нормалізовані значення по кожному з трьох критеріїв оптимальності:

Формула для розрахунків за цим методом має вигляд [16, с.361]:

(8)

дe - відхилення числового значення i-го критерію по по j-му варіанту від ідеальної точки.

Після виконання необхідних розрахунків отримаємо матрицю відхилень числових значень критеріїв від ідеальної точки (таблиця 7).

Таблиця 7

Матриця відхилень числових значень критеріїв від ідеальної точки

Номер варіанту J=1	Відхилення від ідеальної точки			Сумарне відхилення від ідеальної точки
1	1 (1-0)	0,75(1-0,25)	0,25(1-0,75)	2
2	0,8462	0,25	0,125	1,2212
3	0,7692	0	0	0,7692
4	0,3846	0,625	1	2,0096
5	0,1538	1	0,375	1,5288
6	0	0,875	0,5	1,375

Відповідь: як видно з таблиці 7 третій варіант інноваційного проекту є оптимальним при застосуванні методу відхилення від ідеальної точки.

Задача 12. Виберіть з наведених в таблиці 1 один найбільш ефективний інноваційний проект, використовуючи метод згортання критеріїв (дивіться умови задачі 9).

Якщо головним принципом попередніх методів визначення коефіцієнтів важливості критеріїв був принцип їх рівноцінності, то особливістю даного методу є диференціація оцінки коефіцієнтів важливості кожного з включених в економіко-математичну модель критеріїв.

Для нашого випадку скористаємося експертним методом нормування коефіцієнтів важливості різних критеріїв. Зокрема, внаслідок опитування визначено, що ЧДД, ІД та Т_ок були присвоєні такі вагові коефіцієнти як 0,4; 0,4; 0,2 (відповідно .

Для вибору економічно найбільш ефективного інноваційного проекту використовується формула [16, с.362]

, (9)

де ai – коефіцієнт важливості по i-тому критерію,

- числові значення нормалізованого по i-тому критерію j-того варіанту.

Числові значення нормалізованих критеріїв оптимальності по альтернативним варіантам інноваційних проектів наведені в таблиці 8 (для розрахунків скористаємося даними таблиці 6).

Таблиця 8