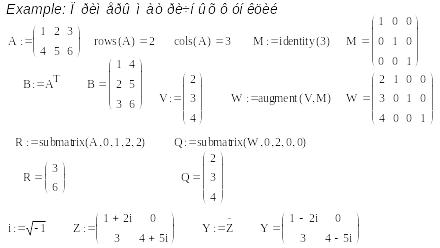Работа с массивами, векторами и матрицами.

Матрицей называется прямоугольная таб­ли­ца из чи­­сел, содержащая некоторое количество m строк и n столбцов, при этом числа m и n на­зываются порядками мат­ри­цы. Если m = n, мат­­рица на­зывается квадратной, а число m = n - ее по­­рядком. Для записи матриц ис­пользуются сле­ду­ю­щие обо­зна­че­ния:

,

г де числа a_ij называются элементами матрицы A. В слу­чае, если m = n и определитель матрицы detA  0, мат­ри­ца A на­зывается невырожденной и для нее можно найти об­рат­ную мат­ри­цу. Обратной по от­но­шению к дан­ной мат­ри­це A называется матрица A^-1, которая, бу­ду­чи умно­женной как справа, так и сле­ва на A, дает еди­­ничную матрицу:

.

Матрица A^T, полученная перестановкой строк со столб­ца­ми в мат­­ри­це A, называется транс­по­ни­ро­ван­ной. Квад­ратная мат­ри­ца A на­зы­ва­ет­ся сим­мет­рич­еской, если A^T = A, и ор­то­го­наль­ной, если A^T A = E.

Вектор – одномерный массив данный, матрица – двумерный массив данных.

В диалоговом окне задаются: Rows – число строк, Columns – число столбцов.

Задается через меню или вызовом шаблона с панели инструментов. Шаблон обрамляющие прямые скобки и темные маленькие прямоугольники, обозначающие места ввода значений (числовых или символьных) для элементов вектора или матрицы.

CTRL+М – вставка шаблона матрицы.

Example:

Можно задать путем ввода элементов – индексированных переменных.

А_0,0:=1 А_0,1:=2 А_1,0:=4 А_1,1:=8, если ORIGIN:=0 (по умолчанию)

А_1,1:=1 А_1,2:=2 А_2,1:=4 А_2,2:=8, если ORIGIN:=1

Значение ORIGIN (номер первой строки (столбца) матрицы или первой компоненты вектора) задается один раз в начале документа и принимается по умолчанию для всего документа.

ВНИМАНИЕ!!! ORIGIN пишется прописными буквами!

Одномерные массивы

общее обозначение элемента А_i, где i – номер элемента в массиве.

Обращение к каждому элементу осуществляется через счетчик

i:=1..n (при ORIGIN:=1),

где n – количество элементов в массиве, или

i:=0..n-1 (при ORIGIN:=0)

Индексация : или

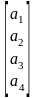
Двумерные массивы

общее обозначение элемента А_i,j, где i – номер строки, j – номер столбца элемента в массиве.

Индексация : 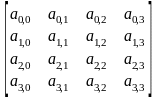или

Обращение к каждому элементу осуществляется через счетчики :

i:=1..n j:=1..n (при ORIGIN:=1), где n – количество элементов в массиве,

или

i:=0..n-1 j:=0..n-1 (при ORIGIN:=0)

Векторные и матричные функции:

lenght (V) – вычисление числа элементов вектора V.

last (V) – вычисление номера последней компоненты вектора V.

max (V) – возвращает максимальный по значении элемент вектора (или матрицы).

min (V) – возвращает минимальный по значении элемент вектора (или матрицы).

Re(V) – возвращает вектор действительных частей вектора в комплексными элементами.

Im (V) – возвращает вектор мнимых частей вектора в комплексными элементами.

Матричные функции:

augment (M1,M2) – объединяет в одну матрицы М1, М2, имеющие одинаковое число строк (объединяются бок о бок).

stack(M1,M2) - объединяет в одну матрицы М1, М2, имеющие одинаковое число столбцов (объединяются сверху вниз).

identity (n) – создает единичную квадратную матрицу n х n.

Re(M) – возвращает матрицу действительных частей матрицы в комплексными элементами.

Im(M) – возвращает матрицу мнимых частей матрицы в комплексными элементами

“ (SHIFT+Э) – задание комплексно-сопряженной матрицы

matrix (m,n,f) – создает матрицу элементов f(i,j), i=0,1..m j=0,1..n, f(i,j) – функция.

diag(V)–создает диагональную матрицу, элементы главной диагонали равны эл-там вектора V.

submatrix(A,ir,jr,ic,jc) – формирует матрицу, которая является блоком матрицы А, расположенным в строках с ir по jr и в столбцах с ic по jc, ir≤jr, ic≤jc.

Обратите внимание на задание номеров строк и столбцов при различной индексации элементов!

Специальные характеристики матриц:

cols(M)–число столбцов матрицы; rows(M)–число строк матрицы; rank(M)–ранг матрицы.

tr(M) – след (сумма диагональных элементов) квадратной матрицы.

mean (M) – среднее значение элементов массива. median(M) –медиана элементов массива.

eigenvals(M) – вектор, содержащий собственные значения матрицы.

Функции преобразования координат:

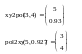– преобразование вектора в декартовых координатах (x=3,y=4) в вектор в полярной системе координат (полярная координата и полярный угол: r=5, φ=0.927)

– преобразование вектора в полярной системе координат (полярная координата и полярный угол: r=5, φ=0.927) в вектор в декартовых координатах (x=3,y=4)

- преобразование вектора в декартовых координатах (x=3,y=4,z=2)

в цилиндрические (r=5, φ=0.927, z=2)

Операции с матрицами: