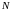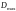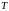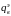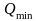4.Основные предпосылки и упрощения для статического расчёта рамы каркаса
Для облегчения расчёта вводятся следующие упрощения:
сквозные элементы (ферма, колонна) заменяются сплошными стержнями эквивалентной жёсткости;
ось эквивалентного ригелю стержня принимается на отметке нижнего пояса фермы;
оси верхней и нижней частей колонны совмещаются, что учитывается введением дополнительных изгибающих моментов в месте изменения сечения колонны;
пролёт рамы принимается по разбивочным осям;
неравномерно распределённая ветровая нагрузка заменяется более простой.
Эквивалентными жесткостям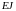и
и
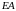задаются из опыта проектирования. Для
статического расчёта рамы важно знать
не сами жёсткости, а их соотношения. Из
опыта проектирования примем значения
изгибных жёсткостей верхней, нижней
колонны и ригеля:
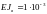кНм2;
кНм2 и
кНм2, а продольные жёсткости
кН. В последствии (после подбора сечений
ригеля и стойки) эти соотношения будут
установлены точно. Если разница
установленных и предварительно принятых
соотношений не превышает 1,5 … 2 раза, то
это неощутимо для результатов статического
расчёта. При большей разнице статический
расчёт рамы подлежит корректировке.
Смещение осей верхней и нижней частей колонны вызывает появление дополнительного изгибающего момента в месте изменения сечения от вертикальных нагрузок, приложенных по оси верхней части колонны. Величина смещений осей:
Нагрузка от веса шатра (опорная реакция фермы):
Дополнительный изгибающий момент от шатровой нагрузки
Аналогично для снеговой нагрузки
Вертикальные крановые нагрузки
приложены с эксцентриситетом
.
При переносе этих сил на ось нижнего
пояса появятся дополнительные изгибающие
моменты: от максимального и минимального
кранового давления:
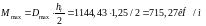
Эксцентриситетом приложения других нагрузок (стенового ограждения, веса подкрановых балок и т.д.) пренебрегаем.
5. Параметры для статического расчёта рамы каркаса
В процессе компоновки, сбора и преобразования нагрузок установлены расчётная схема и другие данные для статического расчёта рамы.
В расчётной схеме постоянные нагрузки, действующие на колонну, обобщены в виде соcредоточенных сил G:
;
;
;
.
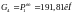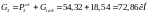Нагрузка
и соответствующий ей момент
возникают при смещении тележки крана
к левой колонне. При этом на правой
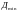колонне возникают нагрузки
и
.
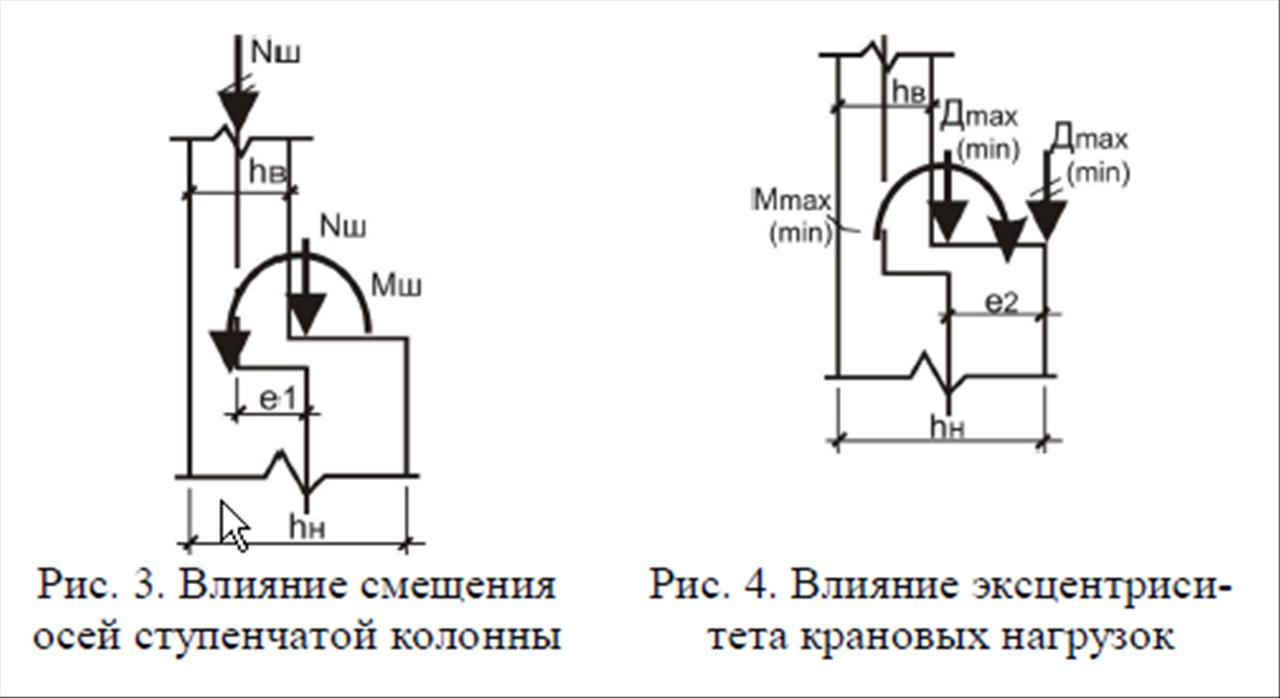
Рис. 5
Параметры для статического расчёта рамы каркаса.
Параметр |
Обозначение |
Величина |
|
/
|
6 36 м 12м 11,73м 6,17 м 1,77м 49,27 кН 72,86 кН
19,57 кН 191,81 кН 42,46 кН/м 9,6 кН/м 1144,47 кН 273,72 кН 33,21 кН 5,623 кН/м
6,653 кН/м 25,148 кН 191,07 кНм 136,08 кНм 715,27 кНм 171,08 кНм |
Таблица расчётных сочетаний усилий
№ сечения |
n |
Расчётное сочетание усилий |
|||||||||||||||
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
1-1 |
1 |
1+(4+7) |
1+(3+5) |
1+(3+6) |
1+9 |
1+10 |
|||||||||||
893,6 |
-1339 |
-73,7 |
-52,1 |
-2291,9 |
-28 |
-2297,9 |
640,3 |
-87 |
87,7 |
-942,1 |
-745,9 |
-125,9 |
-969,7 |
1328,4 |
|||
0,9 |
1+0,9(2+(4+7)+10) |
1+0,9((3+5)+9) |
1+0,9((3+6)+2+9) |
1+0,9((3+5)+9) |
1+0,9(2+(3+6)+10) |
||||||||||||
1857 |
-1540 |
-168 |
-975,48 |
-2145,9 |
74,93 |
-2378,1 |
-238,29 |
-0,31 |
-975,48 |
-2145,9 |
74,93 |
-179,86 |
-2402,9 |
1628,6 |
|||
2-2 |
1 |
1+9 |
1+(3+6) |
1+(3+6) |
1+9 |
1+10 |
|||||||||||
-8,1 |
-942,1 |
-746 |
-654,8 |
-2297,9 |
-87 |
-2297,9 |
-654,8 |
- 87 |
-745,9 |
-942,1 |
-8,1 |
-68,8 |
-969,7 |
-119,3 |
|||
0,9 |
1+0,9((4+7)+9) |
1+0,9(2+(3+6)+10) |
1+0,9((3+6)+2+10) |
1+0,9((3+5)+9) |
1+0,9(2+(3+6)+10) |
||||||||||||
-131,7 |
-1289 |
217 |
-664,13 |
-491,12 |
-119,02 |
-491,12 |
-664,13 |
-119 |
6,44 |
-2145,9 |
-371,63 |
-119,02 |
-491,12 |
-664,2 |
|||
3-3 |
1 |
1+(3+5) |
1+2 |
1+2 |
1+9 |
1+(3+5) |
|||||||||||
41,9 |
-760,1 |
-73,7 |
-324,8 |
515,4 |
-37 |
515,4 |
-324,8 |
-37 |
11,6 |
-753,6 |
-168 |
-73,7 |
-760,1 |
41,9 |
|||
0,9 |
1+0,9(3+5+9) |
1+0,9(2+10) |
1+0,9(2+(4+7)+10) |
1+0,9(2+9) |
1+0,9(2+(3+5)+10) |
||||||||||||
72,91 |
-748,4 |
-34,7 |
-357,2 |
-1006,6 |
-74,02 |
-1013,2 |
-305 |
-116,5 |
-1,66 |
-981,78 |
-257,12 |
-41,8 |
-1000,1 |
-109,8 |
|||
4-4 |
1 |
1+9 |
1+10 |
1+2 |
1+9 |
1+(4+7) |
|||||||||||
-180,9 |
-753,6 |
-16,2 |
-596,1 |
-781,2 |
-47,9 |
-1019,4 |
-525,7 |
-37 |
-16,2 |
-753,6 |
-180,9 |
-73,7 |
-774,7 |
-575,5 |
|||
0,9 |
1+0,9(9+(3+5)) |
1+0,9(2+(4+7)+10) |
1+0,9(2+(4+7)+10) |
1+0,9(9+2) |
1+0,9((4+7)+10+2) |
||||||||||||
-183,8 |
-748,4 |
-59,7 |
-886,5 |
-1013,2 |
-97,69 |
-1013,2 |
-886,5 |
-97,69 |
-26,68 |
-981,78 |
-334,26 |
-97,69 |
-1013,2 |
-886,5 |
|||
