3А. Начинаем внутреннюю итерационную процедуру расчета температуры стенки tст1.

1. Задаемся, согласно приведенным выше рекомендациям, значением температурного напора пар – стенка t₁ и находим t_ст1:

t₁=0  t_ст1= t_н-t₁=191,6-0=191,6С.

2. Рассчитываем коэффициент теплоотдачи со стороны пара:

где: =0,6

_к=_к*_к=0,141*10^-6*880=1,241*10^-4 Па*с.

3. Находим значение температуры стенки труб со стороны мазута:

t_ст2= t_ст1-_п*t₁*(_ст/_ст)=191,6-19269,8*0*(2,5*10^-3/46,5)=191,6С,

где: _ст=(d_н- d_вн)/2=(0,038-0,033)/2=0,0025 м.

4. Определяем средний коэффициент теплоотдачи со стороны мазута:

Для этого определяем теплофизические характеристики мазута при t_ст2=191,6С:

Плотность мазута: _м.ст=(0,881-0,00304*(t_ст2-68))*10³=

=(0,881-0,00304*(191,6-68))*10³=505,256 кг/м³;

Кинетическая вязкость: _м.ст=(10^{10^(9,8555-3,745*log(tст2+273))}-0,8)*10^-6=

=(10^{10^(9,8555-3,745*log(191,6+273))}-0,8)*10^-6=4,95*10^-6 м²/с;

Динамическая вязкость: _м.ст=_м.ст*_м.ст=4,95*10^-6*505,256=2,5*10^-3 Па*с.

После определяем безразмерные комплексы:

Число Прандтля для мазута:

Pr_м=_м* С_рм*_м/_м=3,3*10^-5*2011,24*754,84/0,139=360,4;

Средняя скорость течения мазута в гладких трубах:

Число Рейнольдса: Re_м=W_м*d_вн/_м=0,836*0,033/3,3*10^-5=836;

Разность температур: t₂= t_ст2- t_мср=191,6-109,5=82,1С;

Плотность мазута при t_1м: _1м=(0,881-0,00304*(t_1м-68))*10³=

=(0,881-0,00304*(60-68))*10³=905,32 кг/м³;

Плотность мазута при t_2мопт: _2мопт=(0,881-0,00304*(t_2мопт-68))*10³=

=(0,881-0,00304*(159-68))*10³=604,36 кг/м³;

Коэффициент объемного расширения мазута:

;

Число Грасгофа:

Gr_м=_м*g d³_вн*t₂/²_м=5,03*10^-3*9,81*0,033³*82,1/(3,3*10^-5)²=133688,5;

5. Определяем коэффициент теплопередачи:

6. Вычисляем t_лог и t₁:

t₁=k*t_лог/_п=151,2*71/19269,8=0,557С.

7. Погрешность расчета по первой внутренней итерации:

_t=t₁-t₁/ t₁=0-0,557/0,557=1 не выполняется условие _t0,03…0,05.

3Б. Переходим ко второй внутренней итерации, при этом значению t1 присваивается значение t1.

1. Задаемся, согласно приведенным выше рекомендациям, значением температурного напора пар – стенка t₁ и находим t_ст1:

t_ст1= t_н-t₁=191,6-0,557=191,04С.

2. Рассчитываем коэффициент теплоотдачи со стороны пара:

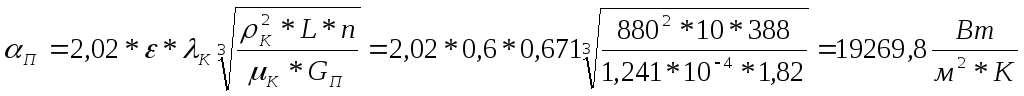
где: =0,6

_к=_к*_к=0,141*10^-6*880=1,241*10^-4 Па*с.

3. Находим значение температуры стенки труб со стороны мазута:

t_ст2= t_ст1-_п*t₁*(_ст/_ст)=191,04-19269,8*0,557*(2,5*10^-3/46,5)=190,4С,

где: _ст=(d_н- d_вн)/2=(0,038-0,033)/2=0,0025 м.

4. Определяем средний коэффициент теплоотдачи со стороны мазута:

Для этого определяем теплофизические характеристики мазута при t_ст2=190,4С:

Плотность мазута: _м.ст=(0,881-0,00304*(t_ст2-68))*10³=

=(0,881-0,00304*(190,4-68))*10³=509 кг/м³;

Кинетическая вязкость: _м.ст=(10^{10^(9,8555-3,745*log(tст2+273))}-0,8)*10^-6=

=(10^{10^(9,8555-3,745*log(190,4+273))}-0,8)*10^-6=4,74*10^-6 м²/с;

Динамическая вязкость: _м.ст=_м.ст*_м.ст=4,74*10^-6*509=2,41*10^-3 Па*с.

После определяем безразмерные комплексы:

Число Прандтля для мазута:

Pr_м=_м* С_рм*_м/_м=3,3*10^-5*2011,24*754,84/0,139=360,4;

Средняя скорость течения мазута в гладких трубах:

Число Рейнольдса: Re_м=W_м*d_вн/_м=0,836*0,033/3,3*10^-5=836;

Разность температур: t₂= t_ст2- t_мср=190,4-109,5=80,9С;

Плотность мазута при t_1м: _1м=(0,881-0,00304*(t_1м-68))*10³=

=(0,881-0,00304*(60-68))*10³=905,32 кг/м³;

Плотность мазута при t_2мопт: _2мопт=(0,881-0,00304*(t_2мопт-68))*10³=

=(0,881-0,00304*(159-68))*10³=604,36 кг/м³;

Коэффициент объемного расширения мазута:

;

Число Грасгофа:

Gr_м=_м*g d³_вн*t₂/²_м=5,03*10^-3*9,81*0,033³*80,9/(3,3*10^-5)²=131734,5;

5. Определяем коэффициент теплопередачи:

6. Вычисляем t_лог и t₁:

t₁=k*t_лог/_п=151,04*71/19269,8=0,5565С.

7. Погрешность расчета по первой внутренней итерации:

_t=t₁-t₁/ t₁=0,557-0,5565/0,5565=0,0005 выполняется условие _t0,03…0,05.