
- •1. Принцип максимума гамильтона – понтрягина 3
- •Принцип максимума гамильтона – понтрягина
- •Использование уравнения риккати для синтеза оптимальных непрерывных су
- •Синтез оптимальных цифровых су с использованием уравнения риккати
- •4. Реализация цифровых регуляторов
- •1. (4.7) Представим в виде:
- •2. Представим (4.8) в виде:
- •Метод декомпозиции.
- •5. Применение функций ляпунова при построении самонастраивающихся систем
- •Список используемой литературы
1. (4.7) Представим в виде:
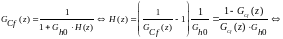
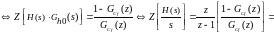
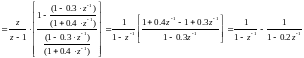 (4.71)
(4.71)
или:
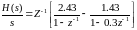 (4.72)
(4.72)
Обратное Z-преобразование будем брать по частям:
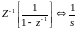 (4.73)
(4.73)
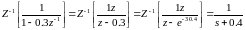 (4.74)
(4.74)
тогда:
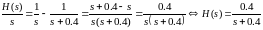 (4.75)
(4.75)
2. Представим (4.8) в виде:
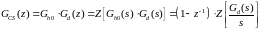 (4.
81)
(4.
81)
или обратная:
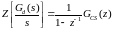 (4.
82)
(4.
82)
Тогда (4. 82) с учетом (4.8) будет иметь вид:
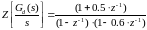 (4.83)
(4.83)
Разложим (4. 83) на простые дроби:
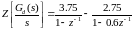 (4.84)
(4.84)
Возьмем обратное Z-преобразование от (4.84):
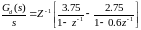 (4.9)
(4.9)
Будем брать по частям:
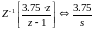 (4.91)
(4.91)
Для поиска последнего слагаемого воспользуемся следующей формой:
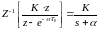 (4.92)
(4.92)
Следовательно:
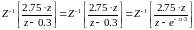 (4.93)
(4.93)
где:
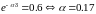 (4.94)
(4.94)
Тогда (4.93) с учетом (4.92) и (4.94) будет равно:
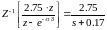 (4.95)
(4.95)
Тогда (4.9) с учетом (4.91) и (4.95) будет равно:
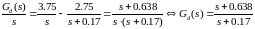 (4.10)
(4.10)
Для подбора электрической схемы преобразуем последнее выражение:
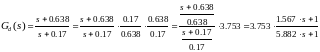 (4.11)
(4.11)
Для подбора электрической схемы воспользуемся атласом для проектирования САР Топчеева Ю.И. Электрическая схема с передаточной функцией вида:
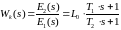 (4.12)
(4.12)
Так
как коэффициент передачи
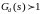 ,
то RC-четырехполюсник
реализуем для коэффициента L0=1,
а в импульсный фильтр дополнительно
включим усилитель с коэффициентом
K=3.753.
Схема имеет следующую структуру:
,
то RC-четырехполюсник
реализуем для коэффициента L0=1,
а в импульсный фильтр дополнительно
включим усилитель с коэффициентом
K=3.753.
Схема имеет следующую структуру:
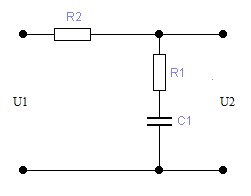
Рис.4.4. RC-четырехполюсник
для передаточной функции вида (4.12)
где её параметры:
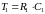
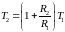
Так как имеется 3 неизвестных и всего два уравнения, зададимся одним любым элементом. Пусть C1=2 мкФ, тогда, решая, получим:
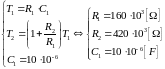
Таким образом, синтезированный ИФ комбинационного типа будет иметь вид:
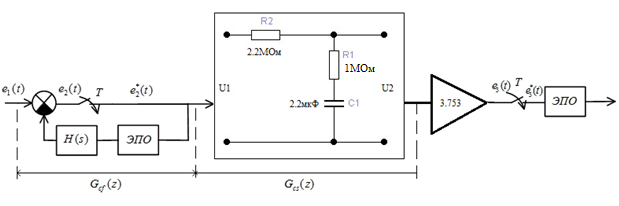
Рис.4.5. Синтезированный ИФ комбинационного типа
Задание 4.2: реализовать цифровой регулятор в виде программы на ЭВМ методами декомпозиции и параллельного программирования.
Дано: передаточная функция регулятора:
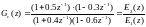 (4.13)
(4.13)
Метод декомпозиции.
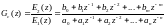 (4.14)
(4.14)
П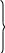 рименительно
к уравнению (4.14) непосредственная
декомпозиция позволяет получить
следующее уравнение:
рименительно
к уравнению (4.14) непосредственная
декомпозиция позволяет получить
следующее уравнение:
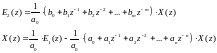 (4.15)
(4.15)
где:
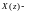 фиктивная
переменная в данный момент времени.
фиктивная
переменная в данный момент времени.
В общем случае, количество накопленных значений сигналов (элементов задержки) равно наибольшему значению из n и m.
Структурная схема непосредственного программирования с использованием декомпозиции при m=n приведена на рисунке (4.7):
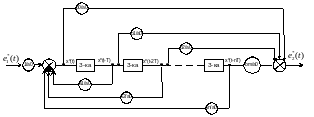
Рисунок 4.6 - Структурная схема реализации ЦР методом декомпозиции при m=n.
Ч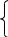 тобы
перейти к непосредственной декомпозиции
введем в уравнении (4.13) фиктивную
переменную, получим следующее:
тобы
перейти к непосредственной декомпозиции
введем в уравнении (4.13) фиктивную
переменную, получим следующее:
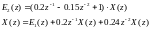 (4.16)
(4.16)
Исходя из системы (4.20) изобразим структурную схему реализации ЦР, имеющую два запоминающих устройства:
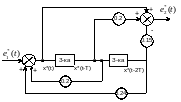
Рисунок 4.8 – структурная схема реализации ЦР (4.13) методом декомпозиции.
Метод параллельного программирования.
При параллельном программировании, передаточная функция цифрового регулятора представляется в виде суммы элементарных дробей соответствующих простейшим передаточным функциям.
Уравнение в этом случае имеет вид:
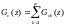 (4.17)
(4.17)
где: Р – наибольшее из чисел n и m. Таким образом, схема параллельного программирования имеет вид:
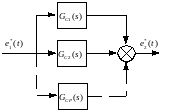
Рисунок 4.9 – структурная схема реализации ЦР методом параллельного программирования.
Передаточные
функции
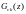 могут
иметь различный вид в зависимости от
нулей и полюсов передаточной функции
ЦР и соотношения между n
и m.
С учетом этого, разделим заданную
передаточную функцию ЦР (4.13) на две
простые функции:
могут
иметь различный вид в зависимости от
нулей и полюсов передаточной функции
ЦР и соотношения между n
и m.
С учетом этого, разделим заданную
передаточную функцию ЦР (4.13) на две
простые функции:
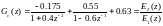 (4.18)
(4.18)
Далее воспользуемся методом декомпозиции и реализуем каждую из простых функций:
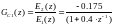
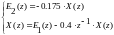
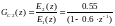
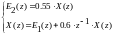
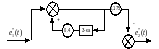
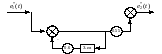
Рис.4.10.1. Структурная схема реализации Gc1
Рис.4.10.2. Структурная схема реализации Gc2
Соединив параллельно схемы на рисунке (4.10.1) и (4.10.2) получим структурную схему вида:
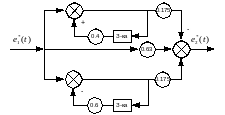
Рисунок 4.11 – структурная схема реализации ЦР методом параллельного
программирования.
