
- •1. Принцип максимума гамильтона – понтрягина 3
- •Принцип максимума гамильтона – понтрягина
- •Использование уравнения риккати для синтеза оптимальных непрерывных су
- •Синтез оптимальных цифровых су с использованием уравнения риккати
- •Реализация цифровых регуляторов
- •Построение самонастаивающихся система методом функций ляпунова
- •Список используемой литературы
Реализация цифровых регуляторов
Задание 1: реализовать цифровой регулятор в виде последовательного импульсного фильтра и RC – четырехполюсника.
Дано: передаточная функция цифрового регулятора:
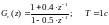 (4.1)
(4.1)
Решение:
Из теории известно, что цифровой регулятор (ЦР) может быть изображен в виде следующей структурной схемы:
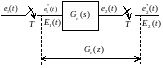
Рисунок 4.1 – структурная схема ЦР.
Входной
сигнал
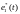 регулятора является последовательностью
чисел
регулятора является последовательностью
чисел
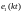 аналитически
представляющих собой выборку значений
сигнала
аналитически
представляющих собой выборку значений
сигнала
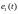 .
ЦР выполняет определенные линейные
преобразования последовательности
и
вырабатывает выходную последовательность
.
ЦР выполняет определенные линейные
преобразования последовательности
и
вырабатывает выходную последовательность
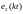 в
виде квантованного сигнала
в
виде квантованного сигнала
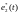 .
.
ЦР может быть реализован в виде последовательного импульсного фильтра, структурная схема которого изображена на следующем рисунке:
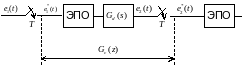
Рисунок 4.2 – структурная схема последовательного импульсного фильтра.
На основании рисунка (4.2) можно записать:
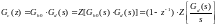 (4.2)
(4.2)
На основании зависимости (4.2) можно записать:
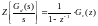 (4.3)
(4.3)
Это соотношение позволяет определить передаточную функцию последовательного ИФ по заданной передаточной функции ЦР.
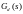 -
этой функции соответствует любой элемент
цепи. Однако, из соображений простоты
предпочтение отдается RC
– четырехполюсникам. Соответственно,
для возможности реализации функции
в
виде RC
– четырехполюсника, передаточная
функция ЦР
-
этой функции соответствует любой элемент
цепи. Однако, из соображений простоты
предпочтение отдается RC
– четырехполюсникам. Соответственно,
для возможности реализации функции
в
виде RC
– четырехполюсника, передаточная
функция ЦР
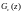 должна
обладать следующими свойствами:
должна
обладать следующими свойствами:
число полюсов должно быть больше или равно числу нулей этой функции;
нули функции могут быть произвольными;
полюсы должны быть простые, положительные, действительные и меньше единицы.
На основании (4.3) перепишем (4.1) в следующем виде:
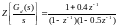 (4.4)
(4.4)
Представим уравнение (4.4) в виде:
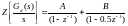 (4.5)
(4.5)
Приравняв (4.5) к (4.4) и решив это уравнение методом неопределенных коэффициентов, получим:
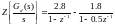 (4.6)
(4.6)
Возьмем обратное Z-преобразования от (4.6):
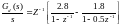 (4.7)
(4.7)
Обратное Z-преобразование от первого слагаемого будет равно:
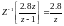 (4.8)
(4.8)
Для определения второго слагаемого воспользуемся следующей формой:
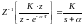 (4.9)
(4.9)
Таким образом, получим:
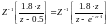 (4.10)
(4.10)
где:
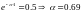 (4.11)
(4.11)
Тогда (4.10), с учетом (4.9) и (4.11), будет равно:
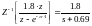 (4.12)
(4.12)
Тогда, с учетом (4.8) и (4.12), перепишем (4.7) в следующем виде:
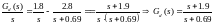 (4.13)
(4.13)
Для подбора схемы корректирующего устройства преобразуем выражение (4.13), получим:
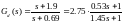 (4.14)
(4.14)
Для подбора корректирующего устройства САР воспользуемся атласом для проектирования САР Топчеева Ю.И. В соответствии с получившейся передаточной функцией:
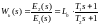 (4.15)
(4.15)
Поскольку
коэффициент передачи функции
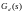 >1,
то RC-четырехполюсник
реализуем для коэффициента
>1,
то RC-четырехполюсник
реализуем для коэффициента
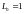 ,
а в импульсный фильтр дополнительно
включаем операционный усилитель с
коэффициентом усиления
,
а в импульсный фильтр дополнительно
включаем операционный усилитель с
коэффициентом усиления
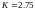 .
Тогда схема корректирующего устройства
имеет вид:
.
Тогда схема корректирующего устройства
имеет вид:
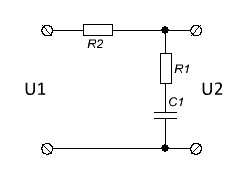
Рисунок 4.3 – RC – четырехполюсник для передаточной функции вида (4.15).
Параметры, которого найдем из следующих формул:
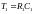
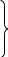 (а)
(а)
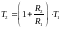 (б)
(б)
П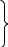 оскольку
имеется три неизвестных (
оскольку
имеется три неизвестных (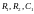 )
и всего два уравнения, зададимся одним
любым элементом. Пусть
)
и всего два уравнения, зададимся одним
любым элементом. Пусть
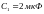 ,
тогда решая систему, получим:
,
тогда решая систему, получим:
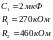
Таким образом, синтезированный последовательный импульсный фильтр будет иметь вид:
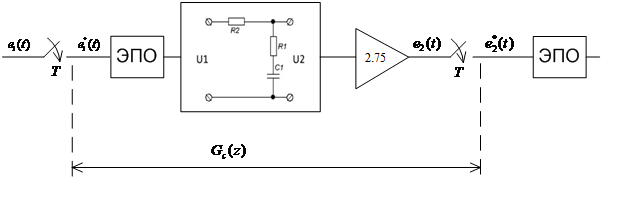
Рисунок 4.4 – синтезированный ИФ последовательного типа.
Задание 2: реализовать цифровой регулятор в виде программы на ЭВМ методами непосредственного и последовательного программирования.
Дано: передаточная функция регулятора:
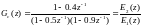 (4.16)
(4.16)
Метод непосредственного программирования.
Из теории известно, что при этом методе передаточная функция ЦР может быть записана в следующем виде:
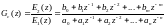 (4.17)
(4.17)
где:

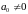 если
если
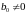
Чтобы перейти к непосредственному программированию, выполним перекрестное умножение в уравнении (4.17), взяв обратное z – преобразование:
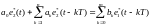 (4.18)
(4.18)
Решение уравнения (4.18) имеет вид:
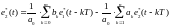 (4.19)
(4.19)
Для составления программы вычисления по уравнению (4.19) необходимы два основных вида операций:
А) накопление данных в памяти ЭВМ;
Б) математические операции на ними.
Запишем выражение (4.19), используя следующую подстановку:
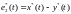
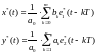
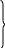
В этом случае непосредственное программирование ЦР выполняется в виде структурной схемы:
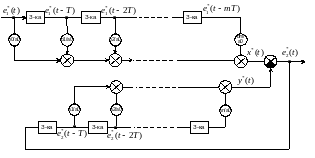
Рисунок 4.5 - Структурная схема реализации ЦР методом непосредственного программирования
Произведём перекрестное умножение в уравнении (4.16), получим:
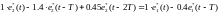 (4.20)
(4.20)
Возьмем от (4.20) обратное z – преобразование, получим:
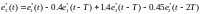 (4.21)
(4.21)
Исходя из уравнения (4.21) изобразим структурную схему реализации ЦР, имеющую три запоминающих устройства:
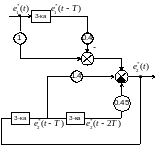
Рисунок 4.6 – структурная схема реализации ЦР с ПФ (4.16) методом непосредственного программирования.
Метод последовательного программирования.
(4.21)
При параллельном программировании, передаточная функция цифрового регулятора представляется в виде суммы элементарных дробей соответствующих простейшим передаточным функциям.
Уравнение в этом случае имеет вид:
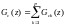 (4.22)
(4.22)
где: Р – наибольшее из чисел n и m. Таким образом, схема параллельного программирования имеет вид:
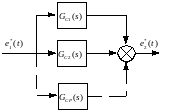
Рисунок 4.9 – структурная схема реализации ЦР методом параллельного программирования.
Передаточные
функции
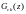 могут
иметь различный вид в зависимости от
нулей и полюсов передаточной функции
ЦР и соотношения между n
и m.
С учетом этого, разделим заданную
передаточную функцию ЦР (4.21) на две
простые функции:
могут
иметь различный вид в зависимости от
нулей и полюсов передаточной функции
ЦР и соотношения между n
и m.
С учетом этого, разделим заданную
передаточную функцию ЦР (4.21) на две
простые функции:
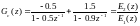 (4.23)
(4.23)
Далее воспользуемся методом декомпозиции и реализуем каждую из простых функций
Получим структурную схему вида:
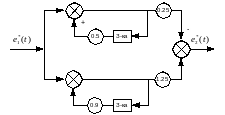
Рисунок 4.10 – структурная схема реализации ЦР методом параллельного
программирования.
