2. Использование уравнения риккати для синтеза оптимальных непрерывных су

Задание: определить оптимальное управление непрерывной системы, используя уравнение Риккати.

Дано: Уравнение движения объекта:

(2.1)

где:

Оптимизирующий функционал имеет вид:

(2.2)

Решение:

Из теории известно, что для оптимизирующего функционала вида:

(2.3)

можно найти оптимальное управление, которое представляет собой линейную функцию от фазовых координат:

_(2.4)

где:

(2.5)

Р(t) – решение уравнения Риккати, которое в алгебраической форме имеет вид:

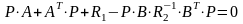(2.6)

где и 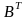найдем из (2.1.1), а и найдем из (2.2):

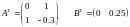(2.7.1)

(2.7.2)

Будем искать решение уравнения Риккати в виде: (2.8)

Подставим (2.1.1), (2.7.1), (2.7.2) в уравнение (2.6), получим:

(2.9)

Подставим (2.7.1), (2.7.2) в (2.6), получим:

Р ешая уравнение (2.10), получим систему:

Решая систему (2.11) с помощью ППП MathCAD, получаем четыре возможные матрицы-решения уравнения Риккати:

(2.12.1)

(2.12.2)

(2.12.3)

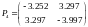(2.12.4)

Проверим каждую из матриц (2.12.1-2.12.4) на не отрицательность. Найдем собственные значения λ каждой из матриц Р₁-P₄:

(2.13)

где Е – единичная матрица.

Произведем подобное вычисление с помощью встроенной функции ППП MathCAD:

(2.14¹)

(2.14²)

(2.14³)

(2.14⁴)

Из полученных пар λ₁ и λ₂ в (2.14¹)- (2.14⁴) видно, что лишь матрица Р₃ удовлетворяет условию не отрицательности. Следовательно, она и является искомой матрицей-решением уравнения Риккати (2.6). Тогда (2.5) примет вид:

_(2.15)

_{Следовательно искомое оптимальное управление (2.4) будет равно:}

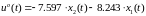_(2.16)

3. Синтез оптимальных цифровых су с использованием уравнения риккати

Задание: определить оптимальное управление цифровой СУ, используя уравнение Риккати.

Дано: Уравнение движения объекта:

(3.1)

где:

(3.1.1)

Оптимизирующий функционал имеет вид:

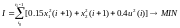(3.2)

Необходимо определить оптимальное управление при

Решение:

Из теории известно, что для оптимизирующего функционала вида:

(3.3)

можно найти оптимальное управление, которое представляет собой линейную функцию от фазовых координат:

(3.4)

где:

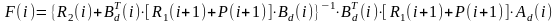; (3.5)

где матрица-решение уравнения Риккати:

(3.6)

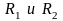где найдем из (3.1.1), а найдем из (3.2):

(3.7.1)

(3.7.2)

Уравнения (3.5) и (3.6) удобно решать в обратном порядке, при этом сначала, в соответствии с уравнением (3.5), вычисляют , а затем с помощью уравнения (3.6) по значениям и находят значение 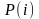и т.д. Значение выбирают равным 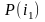, где 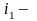произвольно большая величина (в данном случае ). Если терминальная составляющая в оптимизирующем функционале отсутствует, то . Расчеты продолжаются до тех пор, пока значение матрицы F не установится на трёх шагах подряд. Матрица считается установившейся если коэффициенты в ней на этих шагах отличаются только в третьем знаке после запятой.

Зададимся значением:

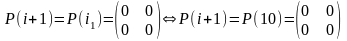(3.8)

Для :

Для :

Для :

Для :

Для :

Для :

Для :

_{Видно, что в последних трёх шагах значение функции F остаётся постоянным с точностью до тысячной доли [см. (3.13.1.),(3.14.1.),(3.15.1)], поэтому расчет останавливаем. Следовательно, оптимальное управление будет равно:}