СОДЕРЖАНИ

1. ПРИНЦИП МАКСИМУМА ГАМИЛЬТОНА – ПОНТРЯГИНА 3

2. ИСПОЛЬЗОВАНИЕ УРАВНЕНИЯ РИККАТИ ДЛЯ СИНТЕЗА ОПТИМАЛЬНЫХ НЕПРЕРЫВНЫХ СУ 7

3. СИНТЕЗ ОПТИМАЛЬНЫХ ЦИФРОВЫХ СУ С ИСПОЛЬЗОВАНИЕМ УРАВНЕНИЯ РИККАТИ 10

4. РЕАЛИЗАЦИЯ ЦИФРОВЫХ РЕГУЛЯТОРОВ 14

5. ПОСТРОЕНИЕ САМОНАСТАИВАЮЩИХСЯ СИСТЕМА МЕТОДОМ ФУНКЦИЙ ЛЯПУНОВА 20

СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ 25

1. Принцип максимума гамильтона – понтрягина 3

2. ИСПОЛЬЗОВАНИЕ УРАВНЕНИЯ РИККАТИ ДЛЯ СИНТЕЗА ОПТИМАЛЬНЫХ НЕПРЕРЫВНЫХ СУ 6

3. СИНТЕЗ ОПТИМАЛЬНЫХ ЦИФРОВЫХ СУ С ИСПОЛЬЗОВАНИЕМ УРАВНЕНИЯ РИККАТИ 9

4. РЕАЛИЗАЦИЯ ЦИФРОВЫХ РЕГУЛЯТОРОВ 13

5. ПОСТРОЕНИЕ САМОНАСТАИВАЮЩИХСЯ СИСТЕМА МЕТОДОМ ФУНКЦИЙ ЛЯПУНОВА 20

СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ 25

1. Принцип максимума гамильтона – понтрягина

Задание: определить оптимальное управление как функцию времени, используя принцип максимума.

Дано: уравнение движения объекта:

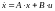(1.1)

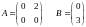(1.1.2)

Управление не ограничено.

Оптимизирующий функционал имеет вид:

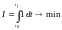(1.1.3)

Начальные и конечные условия:

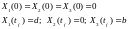(1.1.4)

Изопараметрическое ограничение:

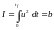(1.1.5)

Решение:

Переведем уравнение (1.1) из матричной формы в систему уравнений:

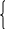
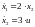(1.2)

Введем вспомогательные функции 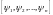и составим Гамильтониан вида:

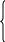
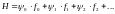(1.3)

где: 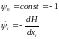(1.4)

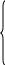
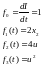(1.5)

Учитывая (1.2), (1.3), получим Гамильтониан вида:

(1.6)

С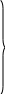 учетом (1.5) определим вспомогательные функции 𝜓:

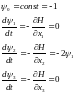
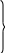или после интегрирования 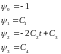(1.7)

Т.к. управление не ограничено, то необходимо найти экстремум функции Гамильтона – Понтрягина. Для этого определим частную производную от него по управлению, получим:

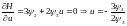
Или с учетом (1.7): 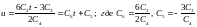(1.8) Перепишем систему (1.3), подставив в неё значение (1.8) и проинтегрируем:

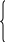
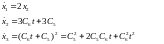(1.9)

Далее получим:

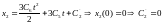
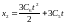(1.10)

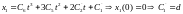
(1.11)

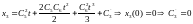
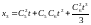(1.12)

Подставив условия (1.1.4), получим:

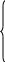
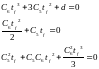(1.13)

Решаем данную систему:

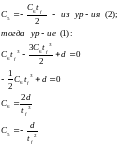(1.14)

Оптимальное управление (1.8), с учетом (1.14), будет равно:

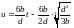(1.15)

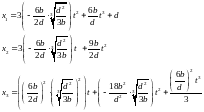(1.16)