Используя закон Кулона, распишем силы
,
где
так как среда воздух,
– сторона квадрата;
где
;
Подставим
уравнения для сил
в
выражение (2):
(3)
Преобразуем выражение (3), найдя общий знаменатель:
(4)
Выражение (4) верно, если числитель равен 0:
(5)
Из
выражения (5), найдем величину заряда
:
Произведём вычисления
Кл.
Ответ:
Кл
= – 96∙10 – 9 Кл = – 96 нКл.
Пример
11. Электрическое поле создано зарядами
нКл
и
нКл,
находящимися на расстоянии 10 см.
Определить напряжённость и потенциал
поля в точке, удалённой от первого
заряда на 12 см, а от второго на 6 см.
Дано:
нКл
=
Кл;
нКл
=
Кл;
;
см
= 0,12 м;
см
= 0,6 м.
Найти:
Решение: В соответствии с условием задачи изобразим вектора напряжённостей, созданные зарядами Q1 и Q2 в точке А (рис. 10):
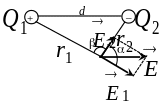
Рис. 10
Согласно принципу суперпозиции
Используя теорему косинусов, перейдём от векторной формы к скалярной:
(1)
Напряжённость
электрического поля, создаваемого
точечными зарядами
и
на расстояниях
и
,
соответственно равны:
так как
Определим
значение
из треугольника со сторонами
,
,
d, используя теорему
косинусов ( рис. 10):
Таким образом,
Произведём
расчёт
:
Н/Кл,
Н/Кл.
Для
расчёта результирующего значения
напряжённости Е подставим значения
в формулу (1):
Н/Кл.
Так как поле создаётся двумя точечными зарядами, то потенциал в рассматриваемой точке следует искать методом суперпозиции. В соответствии с этим
где
– потенциалы в рассматриваемой точке,
созданные зарядами
и
соответственно.
Используя формулу потенциала поля, создаваемого точечным зарядом, получим:
Выполним вычисления:
В.
Ответ:
Н/Кл,
=1500
В.
Постоянный ток Основные законы и формулы
1. Сила постоянного тока
где q –заряд, прошедший через поперечное сечение проводника за время t.
2. Плотность электрического тока
или
где
– площадь поперечного сечения проводника
перпендикулярного направлению тока;
n и q
– концентрация и заряд носителей тока;
– средняя скорость направленного
движения заряженных частиц.
3. Сопротивление однородного проводника
где – удельное сопротивление вещества проводника (табличное данное); l – длина проводника; S – площадь поперечного сечения проводника.
4. Сопротивление системы проводников:
а) при последовательном соединении
,
б) при параллельном соединении
,
где
– сопротивление отдельных проводников,
n – число проводников.
5. Закон Ома:
а) для неоднородного участка цепи
,
б) для
однородного участка цепи (
)
,
З
нак
определяется следующим образом:
1) – + , при переходе в самом источнике от “–” обкладки к
“+” берётся со знаком плюс;
2
)
+ – , при переходе в самом
источнике от “+” обкладки к
“–” берётся со знаком минус;
в) для
замкнутого контура (
)
,
где (
)
– разность потенциалов на концах
участка цепи;
– ЭДС источников тока, входящих в
участок; U12 –
напряжение на участке цепи;
– ЭДС всех источников тока замкнутого
контура; R, r
–соответственно внешнее и внутреннее
сопротивления
.
6. Падение напряжения или напряжение на участке цепи
.
7. Законы Кирхгофа:
а) Первый закон: алгебраическая сумма сил токов, сходящихся в узле, равна нулю.
,
где n – число токов, сходящихся в узле;
б) Второй закон: в замкнутом контуре алгебраическая сумма напряжений на всех участках равна алгебраической сумме электродвижущих сил, действующих в этом контуре.
,
где n
– число участков, содержащих активное
сопротивление, k –
число участков, содержащих источники
тока,
–
сила тока на отдельном участке,
–
активное сопротивление на отдельном
участке,
– ЭДС источников тока на отдельном
участке.
8. Работа, совершаемая электростатическим полем и сторонними силами в участке цепи постоянного тока за время t
.
9. Мощность тока при прохождении по проводнику с сопротивлением R
.
10. Полная мощность цепи – мощность, развиваемая источником тока
.
11. КПД источника тока
12. Закон Джоуля–Ленца
где Q – количество теплоты, выделившееся в проводнике за время t.
Пример
12. Два источника тока с
В,
и внутренними сопротивлениями
Ом,
Ом
соединены как показано на рисунке 11.
Определить:
а) разность потенциалов на участке проводника АB;
б)
выяснить условие, при котором
Дано:
В;
В;
Ом;
Ом.
Найти:
а)
б) условие, когда
?
Решение:
а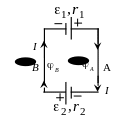
)
Выберем направление тока по часовой
стрелке (рис. 11).
Рис. 11
Разобьем
контур на два неоднородных участка
и
.
Запишем для каждого участка закон Ома
для неоднородного участка цепи:
,
(1)
.
(2)
Решим систему уравнений (1) и (2):
,
либо
.
(3)
Решая
уравнение (3), выразим
:
.
Выполним вычисления:
В.
Тогда
В.
Знак “–” говорит о том, что потенциал точки В больше потенциала точки А, то есть ток течёт в другом направлении.
б) По
условию
.
Следовательно и
Тогда выражения (3) примет вид:
,
или
.
Ответ:
а)
В;
б)
Пример
13. Три источника тока с ЭДС
В,
В,
В и внутренними сопротивлениями
Ом и три реостата с сопротивлениями
Ом,
Ом,
Ом
соединены, как показано на рисунке 12.
Определить силу тока в реостатах.
Дано:
В;
В;
В;
Ом;
Ом;
Ом;
Ом.
Найти:
Р
ешение:
Рис. 12
Силы токов в разветвленной цепи можно определить с помощью правил Кирхгофа. Для этого необходимо составить три уравнения. Перед составлением уравнений необходимо:
а) выбрать произвольно направления токов, текущих через сопротивления, указав их стрелками на чертеже;
б) выбрать направления обхода контуров.
В нашем случае направление токов выберем как на рисунке 12 и обходы контуров по часовой стрелке.
Воспользуемся первым правилом Кирхгофа, учитывая что, ток подходящий к узлу входит в уравнение со знаком “+”, а ток отходящий из узла – со знаком “–” .
Для узла А
,
или
При составлении уравнений по второму правилу Кирхгофа учитываем следующие правила знаков:
если ток по направлению совпадает с выбранным направлением
обхода
контуров, то соответствующее произведение
входит в уравнение со знаком “плюс”,
иначе – со знаком “минус”;
если при обходе контура приходится идти от “–” к “+” внутри
источника тока, то соответствующая входит в уравнение со знаком “плюс”, иначе – со знаком “минус”.
Для контуров
ACDBА:
, (1)
CDFEС:
.
(2)
Подставив
значения
в соотношения (1) и (2), получим систему
уравнений:
.
Решим эту систему с помощью определителей. Для этого запишем её в виде:
Искомые токи найдем по формулам:
;
;
Найдем
определители
:
Таким образом
А;
А;
А.
Знак
“минус” у тока
говорит о том, что направление тока на
рисунке 12 было указано противоположно
истинному, т.е. ток идет от узла B
к узлу A.
Ответ:
;
;
.
Пример
14. Три одинаковых источника тока с
ЭДС
каждый соединены одинаковыми полюсами
параллельно (рис. 13) и создают в цепи
ток
.
Определить коэффициент полезного
действия батареи, если внутреннее
сопротивление каждого источника тока
.
Дано:
В;
Ом;
.
Н
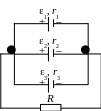айти:
Решение:
Рис. 13
При параллельном подключении одинаковых источников тока их общая электродвижущая сила равна ЭДС одного источника. В то же время батарея источников создаёт разветвлённый участок цепи, общее сопротивление которого определяется:
(1)
Так
как в задаче группа параллельно
соединённых элементов образована
батареей из трёх источников тока с
общим сопротивлением
,
а
,
формулу (1) можно записать в виде
(2)
Батарея
источников тока замыкается потребителем
электроэнергии, сопротивление которого
.
Тогда на основании закона Ома для
замкнутой цепи
.
Отсюда
,
(3)
где U – разность потенциалов на зажимах батареи источников электроэнергии.
Коэффициент полезного действия батареи
.
(4)
Из (3) следует, что
.
(5)
Подставив (2) в (5) и затем в (4), получим:
.
Выполним вычисления:
.
Ответ:
