2.6 Исследование точности системы

Чтобы определить границу устойчивости системы воспользуемся инструментом GUI-интерфейс SISO-Design Tool из пакета прикладных программ Control System Toolbox

>> w=tf([0.00816 0.24],[0.0000017408 0.0002816 0.000576 0.0328704 0])

Transfer function:

0.00816 s + 0.24

---------------------------------------------------------

1.741e-006 s^4 + 0.0002816 s^3 + 0.000576 s^2 + 0.03287 s

>>p=zpk('p'); w=(12*0.02*(0.034*p+1))/(0.32*(0.02*0.01*0.034*0.08*p^4+0.02*0.08*p^3*(0.034+0.01)+0.02*p^2*(0.08+0.01)+(0.08*(0.034+1)+0.02)*p))

Ноль/Полюс/Увеличение:

46875 (p+29.41)

----------------------------------

p (p+114.9) (p^2 + 14.49p + 1643)

На основе нашего zpk объекта вызовем SISO-Design Tool командой Sisotool(w)

>> sisotool(w)

Рисунок 12 - Полученный корневой годограф

_{Передвинем красным курсором по годографу (Рисунок 12) до пересечения с мнимой осью, и определим коэффициент усиления, при котором система находится на границе устойчивости (Рисунок 13):}

Рисунок 13 - Корневой годограф на границе устойчивости

В результате мы нашли коэффициент усиления, при котором наша система находится на границе устойчивости.

В нашем случае он равен 0,124

Затем мы задали значения К_РС=0, 5 и К_РС=0,1 (Рисунок 14, Рисунок 15) и определили значения полюсов:

Рисунок 14 - Корневой годограф САУ, при К_РС=0,5

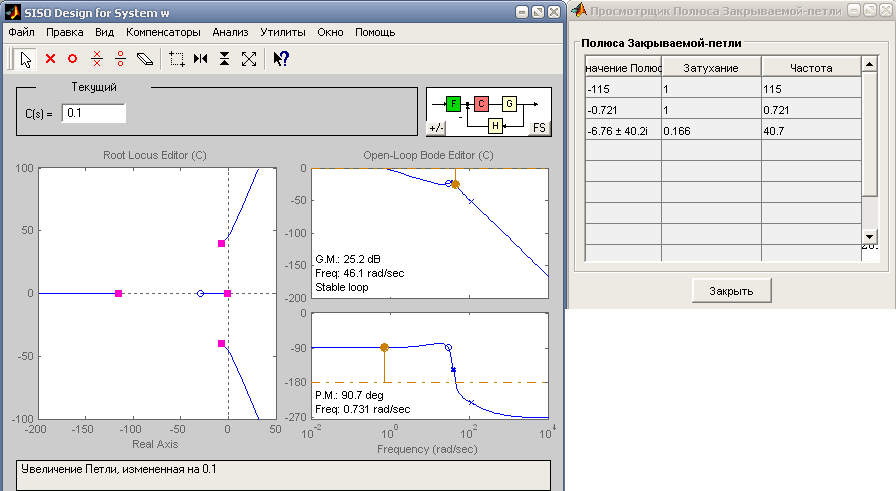
Рисунок 15 - Корневой годограф САУ, при К_РС=0,1

На основе использования метода корневого годографа получили области значений коэффициента усиления, при которых система автоматического управления является устойчивой.

2.7 Расчет частотных характеристик для сау

Передаточная функция неизменяемой части объекта имеет вид:

Передаточная функция разомкнутой исходной системы имеет вид:

(2.5)

Построим логарифмические частотные характеристики (Рисунок 16)

>> w=tf([0.00816 0.24],[0.0000017408 0.0002816 0.000576 0.0328704 0])

Transfer function:

0.00816 s + 0.24

---------------------------------------------------------

1.741e-006 s^4 + 0.0002816 s^3 + 0.000576 s^2 + 0.03287 s

>> bode(w)

Рисунок 16 - Диаграмма Боде

Чтобы построить переходную характеристику (Рисунок 17) воспользуемся командой:

>> step(w)

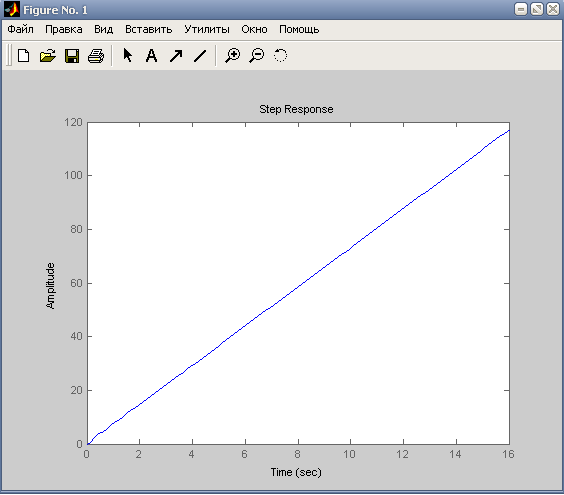
Рисунок 17 - Переходная характеристика

2.8 Выявление систематических ошибок

Передаточная функция замкнутой системы по ошибке от управления имеет вид:

(2.8)

Передаточная функция замкнутой системы по ошибке от возмущения имеет вид:

(2.9)

Для определения точности мы воспользовались методом систематических ошибок. Так как воздействие по каналу управления и возмущения постоянны, для определения величины ε_уст(t) в установившемся режиме необходимо определить коэффициенты статических ошибок по этим каналам, на основании передаточных функций ошибок, необходимо найти лишь первые коэффициенты ошибок согласно выражений:

С_о=W_ε(Р)|S=0

С_of=W_fε(P)|S=0

Для этого приравняли р=0, в выражениях W_ε(p) и W_fε. Так как числитель этих выражений имеет множитель в виде р, то соответственно и коэффициенты ошибок С_о=0; С_of=0, а соответственно ошибка

ε_уст(t)=С_о*X(t)+C_оf*f(t)=0 (2.12)

Таким образом САУ не имеет ошибки в установившемся режиме.