4.2. Перечень примерных вопросов к экзамену по математической сттистике

1. Измерение социальных явлений и процессов.

2. Измерительные шкалы: номинальные, ранговые (порядковые) и интервальные.

3. Выборочный метод статистического исследования.

4. Генеральная и выборочная совокупности. Репрезентативность выборочной совокупности.

5. Случайный отбор и его виды. Простой случайный бесповторный отбор и простой случайный повторный отбор.

6. Типический, механический и серийный отбор

7. Вариационный ряд. Эмпирическая функция распределения.

8. Гистограмма и полигон.

9. Выборочные характеристики. Среднее значение выборочной случайной величины. Выборочная дисперсия и среднеквадратическое отклонение.

10. Точечные оценки неизвестных параметров распределения по выборке.

11. Интервальные оценки неизвестных параметров распределения по выборке.

12. Доверительная вероятность. Доверительные интервалы.

13. Задачи интервального оценивания параметров нормального закона распределения.

14. Расчет объема выборочной совокупности.

15. Проверка статистических гипотез. Понятие статистической гипотезы. Уровень значимости. Нулевая гипотеза.

16. Проверка гипотезы о равенстве средних.

17. Проверка гипотезы о законе распределения.

18. Ранговые критерии проверки статистических гипотез: Ван-дер-Вардена, Уилкоксона, знаков.

19. Понятие корреляционной зависимости между выборочными случайными величинами.

20. Связь номинальных признаков. Таблицы сопряженности.

21. Коэффициент ассоциации Пирсона и Юла. Коэффициент взаимной сопряженности Пирсона-Чупрова. Коэффициент корреляции знаков.

22. Связь порядковых признаков. Коэффициенты корреляции рангов Спирмена и Кендэлла.

23. Связь количественных признаков. Корреляционная таблица. Линейный коэффициент корреляции. Корреляционное отношение.

24. Уравнение регрессии.

4.3. Тест по курсу

1. Предлагаются следующие оценки математического ожидания , построенные по результатам четырех измерений :

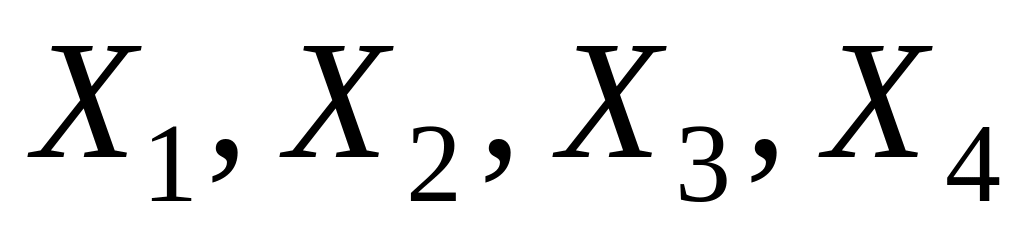А) Б)

В) Г)

Д) .

Из них несмещенными оценками являются:

а

б

в

г

д

2. Дисперсия каждого измерения в предыдущей задаче есть . Тогда наиболее эффективной из полученных в первой задаче несмещенных оценок будет оценка

а

б

в

г

д

3. На основании результатов независимых наблюдений случайной величины X, подчиняющейся закону Пуассона, построить методом моментов оценку неизвестного параметра 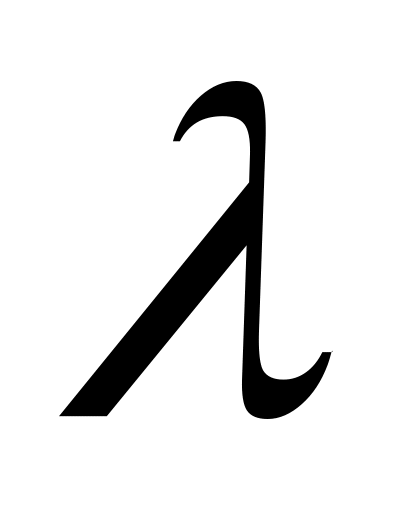распределения Пуассона

	0	1	2	3	4	5
	2	3	4	5	5	3

а) 2.77; б) 2.90; в) 0.34; г) 0.682; д) нет правильного ответа

а

б

в

г

д

4. Полуширина 90% доверительного интервала, построенного для оценки неизвестного математического ожидания нормально распределенной случайной величины X для объема выборки n=120, выборочного среднего =23 и известного значения =5, есть

а) 0.89; б) 0.49 ; в) 0.75; г) 0.98; д) нет правильного ответа

а

б

в

г

д

5. Дополните. … - число, показывающее, сколько раз значение признака встречается в выборке.

6. Дополните. … - отношение частоты значения признака к объему выборки .

7. Отметьте правильный ответ. Сумма частот выборочных значений признака равна:

1) единице 2) объему выборки 3) 4)

8. Отметьте правильный ответ. Перечень значений признака, расположенных в порядке возрастания, и соответствующих им частот (или относительных частот) - это:

1) дискретный ряд 2) статистический ряд 3) вариационный ряд 4) интервальный ряд

9. Отметьте правильный ответ. Таблица называется:

Интервалы			…
Частоты			…

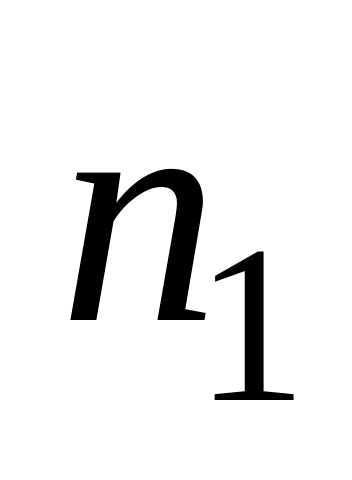
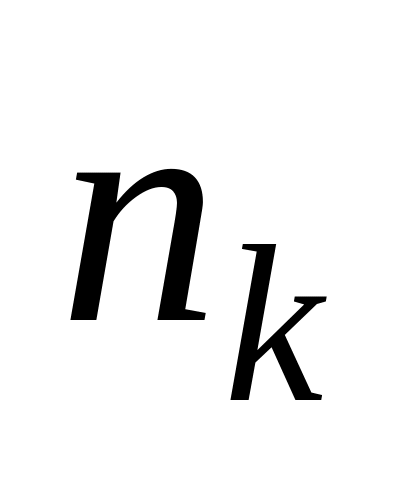
1) дискретный ряд 2) статистический ряд 3) вариационный ряд 4) интервальный ряд

10. Отметьте правильный ответ. Ломаная, отрезки которой соединяют точки с координатами , где - значение признака, - частота:

1) полигон 2) гистограмма 3) многоугольник распределения 4) кумулята

11. Отметьте правильный ответ. Фигура, составленная из прямоугольников с основаниями, равными интервалам значений признака, и высотами, равными соответствующим частотам:

1) полигон 2) гистограмма 3) многоугольник распределения 4) кумулята

12. Выборочное среднее значение выборки вычисляется по формуле …

13. Выборочное среднее значение признака для сгруппированных данных вычисляется по формуле …

14. Отметьте правильные ответы. Показатель степени изменчивости признака в выборке:

1) выборочная дисперсия 2) выборочный коэффициент асимметрии

3) выборочное среднее квадратическое отклонение 4) размах выборки

15. Отметьте правильный ответ. Выборочная дисперсия при малом объеме выборки:

1) 2) 3) 4)

16 Отметьте правильный ответ. Длина доверительного интервала уменьшается с увеличением:

1) выборочных значений 2) объема выборки

3) доверительной вероятности 4) выборочного среднего

17. Отметьте правильный ответ. Длина доверительного интервала с увеличением объема выборки:

1) уменьшается 2) увеличивается 3) не изменяется 4) колеблется

18. Отметьте правильный ответ. Обозначение - это дисперсия:

1) исправленная выборочная 2) выборочная 3) генеральная 4) нормального распределения

19. Отметьте правильный ответ. Несмещенная оценка математического ожидания признака:

1) 2) 3) 4)

20. Отметьте правильный ответ. Несмещенная оценка дисперсии признака: