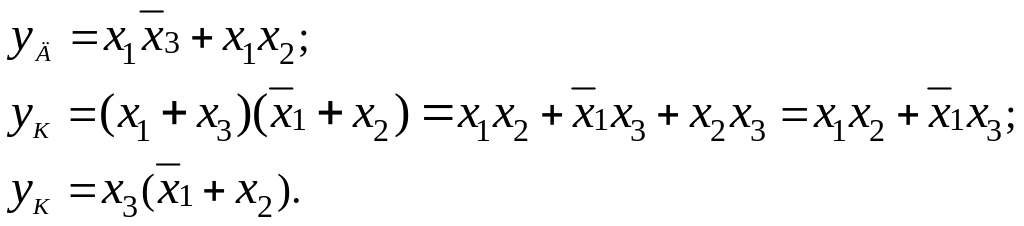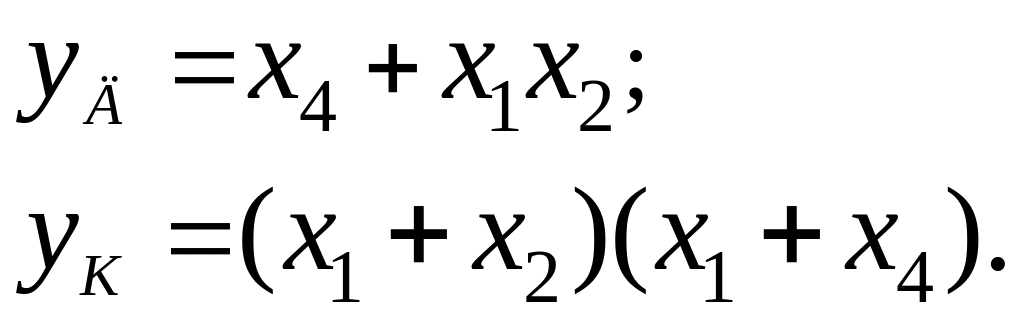Лекция 1.

1. Алгебра логика

   1. Логические функции

	0	1
	0	0
	0	1
	1	0
	1	1

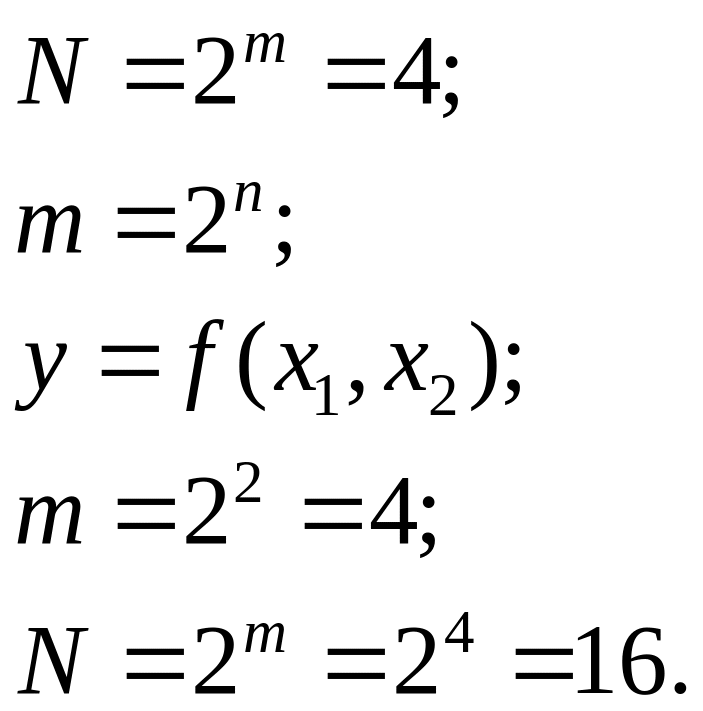
	0101 0011	Функции
	0000
	0001	конъюнкция (И):
	0010	отрицание обратной импликации:
	0011	повторение
	0100	отрицание импликации:
	0101	повторение
	0110	исключающее ИЛИ: ; неравнозначность:
	0111	дизъюнкция (ИЛИ):
	1000	функция Пирса (ИЛИ НЕ):
	1001	равнозначность, эквиваленция:
	1010
	1011	импликация:
	1100
	1101	обратная импликация
	1110	функция Шеффера:
	1111

2. Булева алгебра

Булева алгебра – это математический инструмент, позволяющий описать связи между входом и выходом логических схем при помощи алгебраический функций, то есть булевыми выражениями.

Аксиомы

Дизъюнкция: Конъюнкция:

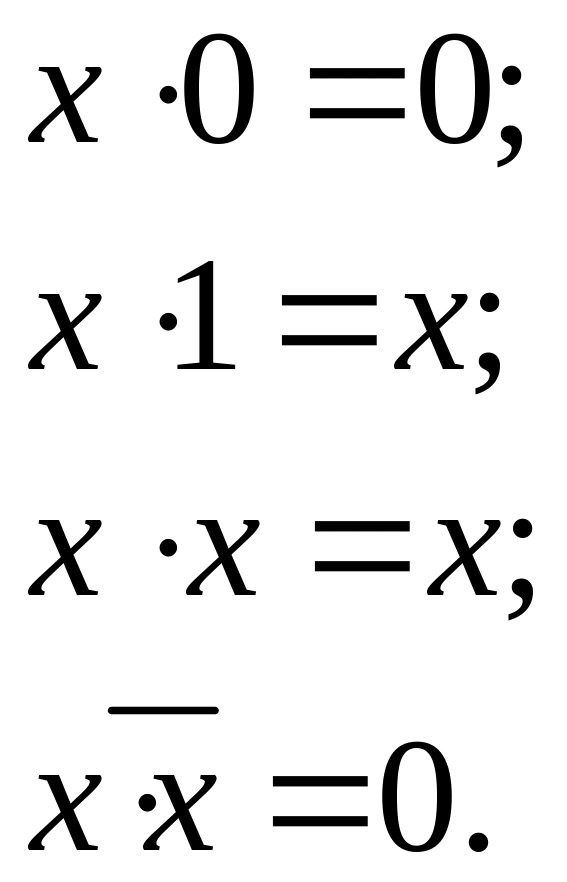
Законы алгебры логики

1.Комутативность (переместительный закон)

2.Ассоциативность (сочетательный закон)

3.Дистрибутивность (распределительный закон)

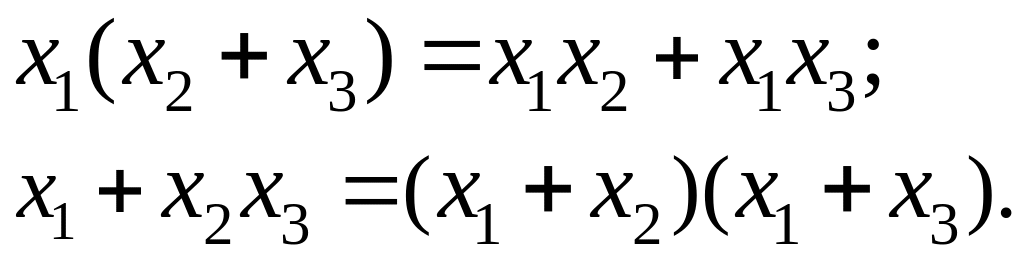
4.Поглощение

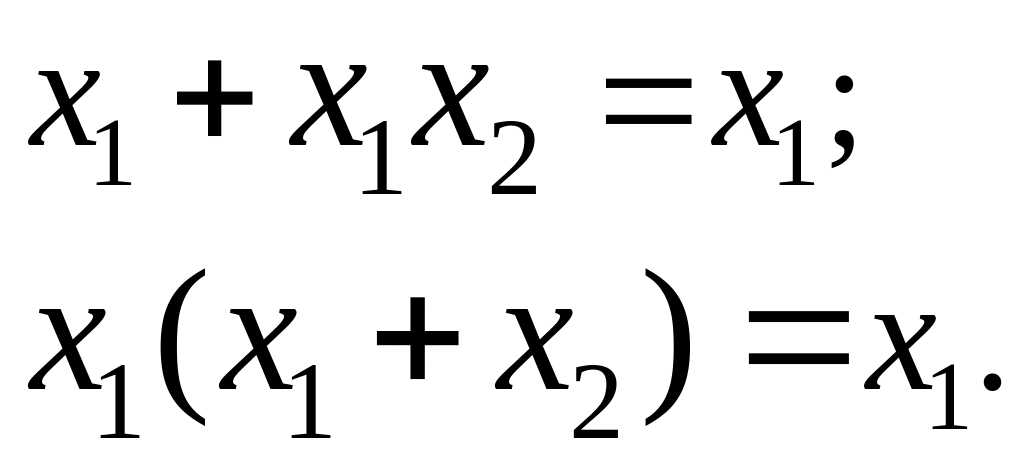
5.Склеивание

6.Замещение

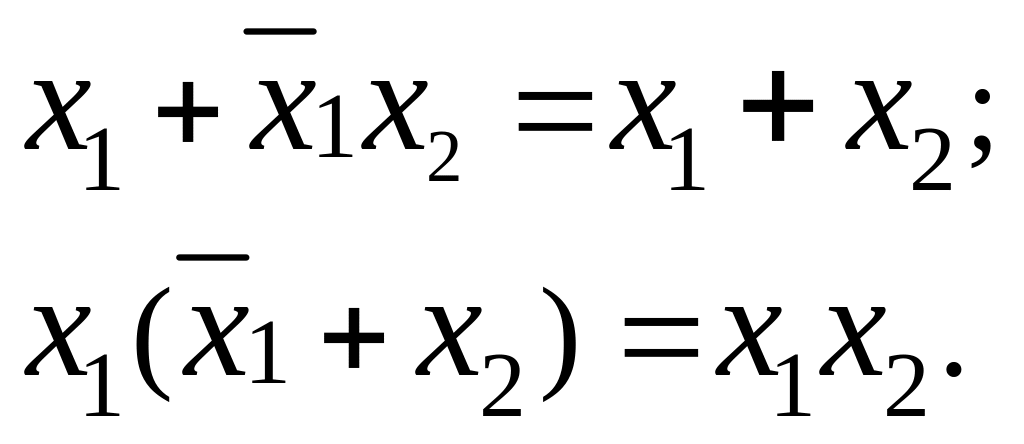
7.Выявление

8.Отрицание (теорема Моргана)

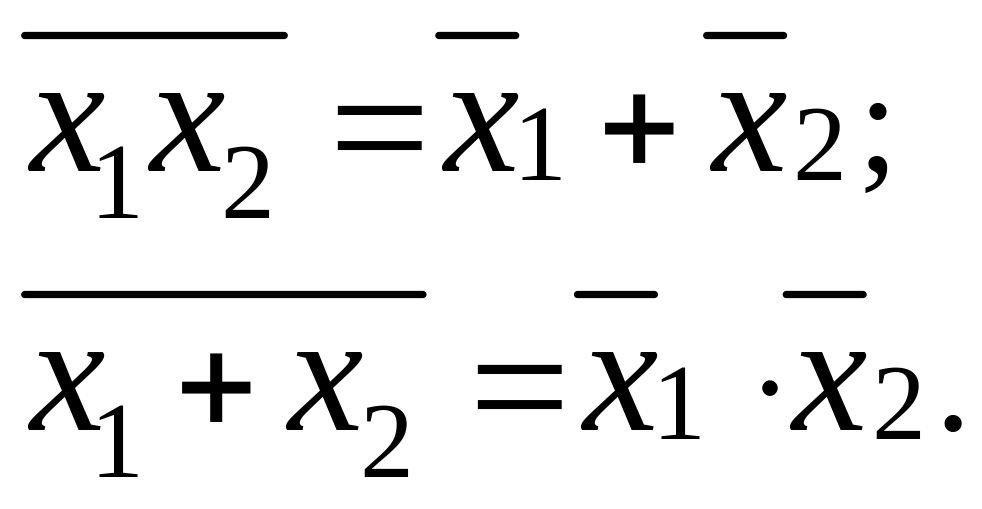
Теорема Шеннона

3. Стандартные формы

	01010101
	00110011
	00001111
	01011001

Дизъюнктивная нормальная форма (ДНФ) – это сумма произведений, когда функция принимает значение единицы, при чем если 1 – без инверсии, если 0 – с инверсией.

Если в каждый минтерм входят все переменные, получаем совершенную конъюнктивную нормальную форму (СДНФ).

Конъюнктивная нормальная форма (КНФ) – произведение сумм, когда функция принимает значение нуля, при чем если 1 – с инверсией, если 0 – без инверсии.

Если в каждый макстерм входят все переменные, получаем совершенную конъюнктивную нормальную форму (СКНФ).

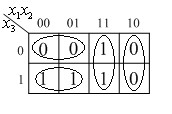
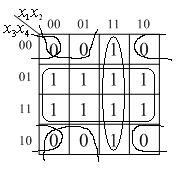
4. Минимизация логических функций

	01010101
	00110011
	00001111
	00011011

Метод карт Карно (диаграмм Вейча)