
- •«Теоретические основы проектирования технологических процессов ракетных двигателей»
- •1. Понятие об изделии и его элементах (детали и сборочные единицы)
- •2. Рабочий чертеж и характеристики детали
- •3. Классификация поверхностей детали и заготовки
- •4. Производственный и технологический процессы
- •Типы производства и их влияние на тп механической обработки
- •Количество партий запуска в год
- •5.1. Особенности производств в различных типах серийности
- •6. Основы базирования
- •6.1. Понятие о базах и базировании
- •6.2. Схема расположения опорных точек на поверхности призмы
- •6.3. Классификация баз
- •6.4. Способы базирования
- •6.5. Установка и погрешность установки
- •6.6. Принципы базирования в технологии
- •7. Точность и погрешность. Категории точности
- •8. Условия обеспечения точности выполняемого размера (параметра)
- •9. Способы достижения заданной точности размеров
- •10. Структура погрешности размеров, выполняемых в операции
- •11. Структура погрешности установки
- •11.1. Влияние деформаций установочной базы на ωу.
- •11.2. Неточность размера базовых поверхностей и погрешность их
- •11.3. Влияние погрешностей приспособлений и выбора баз на ωу
- •11.4. Влияние выбора схемы установки вала в призму на величину ωу
- •12. Причины возникновения погрешности ωм.О, связанные с методом обработки
- •12.1. Погрешности из-за податливости элементов технологической системы
- •12.2. Погрешности, вызываемые неточностью оборудования
- •12.3. Погрешности, возникающие в связи с износом инструмента
- •12.4. Погрешности обработки, связанные с нагревом элементов тс
- •12.5. Погрешности, связанные с деформацией заготовок
- •12.6. Влияние на точность обработки погрешностей настройки станков
- •13. Технологические размерные расчеты
- •14. Выявление размерных цепей и порядок их решения
- •14.1. Общие указания
- •14.2. Порядок решения размерных цепей
- •15. Технически достижимая и средне-экономическая точность
- •16. Категории и значения припусков
- •16.1. Структура min операционного припуска
- •16.2. Неравномерность припуска при обработке плоских торцевых и цилиндрических поверхностей
- •16.3. Методы определения операционных припусков
- •17. Операционные допуски и правила их выбора
- •18. Методика проектирования тп
- •18.1. Классификация технологических процессов, используемых
- •18.2. Технологичность конструирования изделия и основные направления её повышения
- •18.3. Пример разработки тп
- •19. Методика проектирования тп механической обработки
- •19.1. Понятие о технической подготовке производства
- •19.2. Виды технологических процессов (гост 3.1109-82)
- •19.3. Технология групповой обработки (гост 14.00483)
- •19.4. Исходные данные для проектирования тп
- •19.5. Выбор заготовки
- •19.6. Разработка плана операций
- •19.7. Определение последовательности обработки поверхностей заготовки
- •19.8. Выбор баз
- •19.9 Формирование операций и этапов тп
- •19.10. Разработка тт к выполняемым операциям
- •19.11. Выбор оборудования
- •19.12. Автоматизация проектирования тп (аптп)
- •20. Законы теории вероятностей в технологии машиностроения
- •20.1. Проявление различных погрешностей из рассмотренных выше
- •20.2. Законы распределения размеров (или их погрешностей)
- •20.3. Выявление закона распределения в условиях выполняемой операции
- •20.4. Анализ точности обработки с помощью нормального закона
- •20.5. Метод точечных диаграмм
- •21. Вопросы экономики при проектировании тп
- •21.1. Нормирование и норма времени
- •21.2. Экономическое обоснование вариантов выполнения операции
- •21.3. Сравнение вариантов операций по трудоемкости
- •21.4. Сравнение вариантов операций по технологической
- •21.5. Оценка экономической эффективности дополнительных капитальных вложений
20.2. Законы распределения размеров (или их погрешностей)
Размеры и их погрешности в партии заготовок, обработанные по настройке есть случайные величины, и поэтому их распределение в полях рассеивания описывается законами теории вероятностей.
Знание этих законов позволяет:
- прогнозировать ход операции, своевременно вмешиваясь в него с целью не допустить брак;
- дать заключение о точностных возможностях применяемого метода обработки и их соответствия требуемой точности изготовления;
- выполнить динамическую, более оптимальную настройку режущего инструмента.
Для анализа точности обработки в технологии машиностроения находят применение следующие законы теории вероятностей (рисунок 48).
- Закон равной вероятности (рисунок 48а)
- Закон возрастающей вероятности (рисунок 48б)
- Закон треугольника (закон Симпсона) (рисунок 48в)
- Нормальный закон распределения (закон Гаусса) (рисунок 48г)
- Закон Рэлея (рисунок 48д)
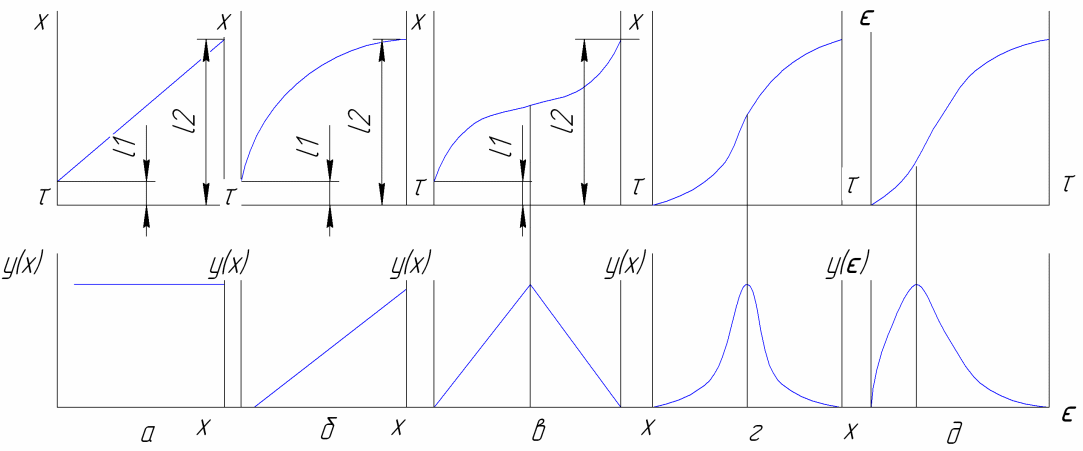
Рис. 48. Законы распределения: х – случайные значения размера
τ – время; у – плотность вероятности
Верхние графики законов являются функциями распределения - интегральной формой закона, а нижние – представляют плотность вероятности – дифференциальную форму закона. Последняя обычно и используется для анализа точности обработки.
Представленные законы проявляются в зависимости от характера выполняемой операции (метод обработки, вид параметра, его действительная точность).
Так, например, закон равной вероятности описывает распределение размеров в поле рассеяния под влиянием износа резца. Закон Рэлея описывает распределение существенно-положительных погрешностей (несоосности, биения, разностенности, значения их случайных величин – ε).
20.3. Выявление закона распределения в условиях выполняемой операции
Чтобы выяснить какой закон описывает точность выполнения действительного параметра в конкретной операции, поступают следующим образом. Сначала отбирается группа Nшт заготовок. На основании результатов измерения рассчитывают регион R практического распределения размеров: Rmax=Amax- Amin,
 где
Amax
, Amin
– действительные предельные значения
размеров в группе. Затем величина R
разделяется на участки и определяются
Ai
– средний
размер; i
– номер
участка и подсчитывают количество
попаданий ni
размеров в тот или иной интервал и
определяют частость ni/N.
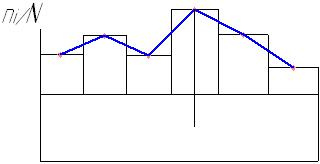
Исходя из этих данных строят гистограмму
практического распределения (см. эскиз).
где
Amax
, Amin
– действительные предельные значения
размеров в группе. Затем величина R
разделяется на участки и определяются
Ai
– средний
размер; i
– номер
участка и подсчитывают количество
попаданий ni
размеров в тот или иной интервал и
определяют частость ni/N.
Исходя из этих данных строят гистограмму
практического распределения (см. эскиз).
Рис. 49
Если увеличивать число деталей N в группе, и уменьшать размер участков, то ломаная линия гистограммы – практического распределения становится всё более плавной, приближаясь к графику математического закона, а частость ni/N – к выражению плотности распределения Р(А), где А- случайные величины.
20.4. Анализ точности обработки с помощью нормального закона
Распределение размеров по закону Гаусса в партии заготовок, обрабатываемых по настройке, объясняется влиянием на точность только случайных погрешностей (при отсутствии среди них какой-либо доминирующей). Это связано с известным положением теории вероятностей о том , что сумма большого числа взаимно независимых случайных слагаемых при ничтожно малом и одинаковом влиянии каждой на их сумму подчиняется именно закону нормального распределения.
Анализ точности обработки с использованием закона Гаусса выполняется в такой последовательности. Получив статистические данные по группе обработанных заготовок, определяют регион R и средние значения интервалов хiср, рассчитывают математическое ожидание М(х) и величину σ:
;![]() ;
;![]()
где обозначении всех величин приведены выше.
Зная
![]() и Б
и задаваясь
различными значениями хi,
рассчитывают плотность вероятности
у(х)
и получают кривую закона и ограничиваемую
ей площадь:
и Б
и задаваясь
различными значениями хi,
рассчитывают плотность вероятности
у(х)
и получают кривую закона и ограничиваемую
ей площадь:
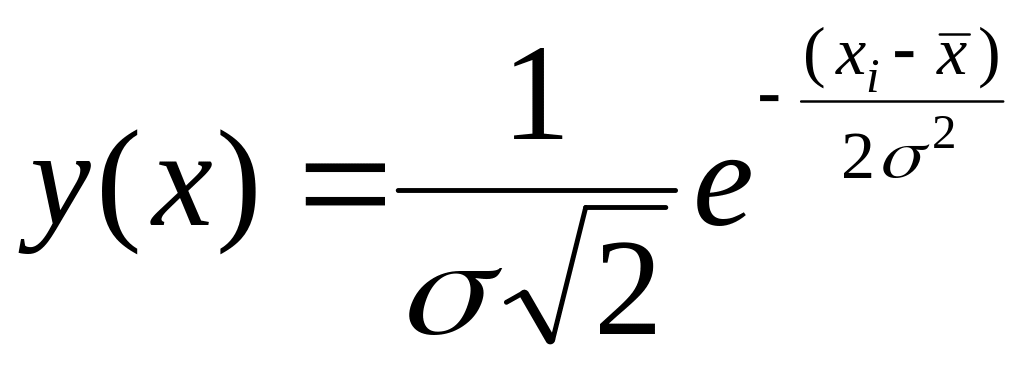 .
.
Площадь под кривой этого закона уходит в бесконечность, что соответствует 100% возможных значений х. Но обычно в практике используется для анализа точности только площадь, ограниченная полем 6σ, т.е. ω=6σ. В интервале ±3σ находится 99,73% площади, ей и ограничиваются.
Собственно
анализ точности выполняемой операции
осуществляется таким образом. На график
закона в том же масштабе накладывается
поле допуска заданного размера
![]() (для валов). Если инструмент настраивался
по среднему размеру поля допуска, т.е.
хА
=АЗС =АЗmax
– TA/2,
то хН
служит ориентиром для расположения
поля допуска в виде ±ТАз/2
(см. эскиз).
(для валов). Если инструмент настраивался
по среднему размеру поля допуска, т.е.
хА
=АЗС =АЗmax
– TA/2,
то хН
служит ориентиром для расположения
поля допуска в виде ±ТАз/2
(см. эскиз).
О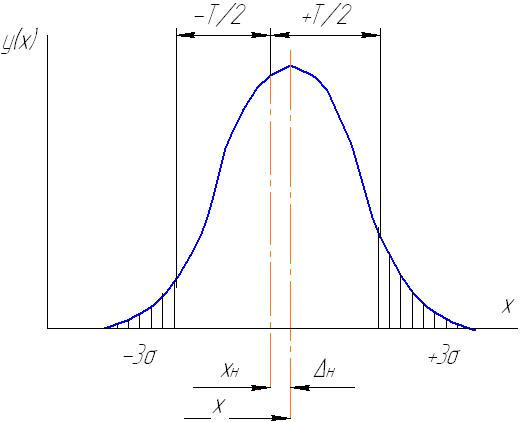 ставшиеся
за границами поля допуска заштрихованные
площадки представляют брак, определяемый
в % к общей площади под кривой. Величину
брака с высокой точностью определяют
с помощью функций Лапласа, приводимых
в справочниках.
ставшиеся
за границами поля допуска заштрихованные
площадки представляют брак, определяемый
в % к общей площади под кривой. Величину
брака с высокой точностью определяют
с помощью функций Лапласа, приводимых
в справочниках.
Погрешность метода обработки по результатам анализа точности операции рассчитывается по формуле
ωГС=2ΔН+6σi=2 ΔН+ωi
Рис. 50
где ΔН – систематическая постоянная величина;
σi – среднее квадратичное отклонение определяемое в данной i – ой операции;
ωi – поле рассеивания размеров в i-ой операции.
В заключении необходимо отметить, что в условиях обработки больших партий заготовок закон Гаусса в «чистом» виде не встречается, а имеет место комбинация законов. Её выявляют построением точностных диаграмм (см. ниже).
