Тема 5. Анализ дисперсности суспензий и эмульсий

Количественной оценкой дисперсности является функция распределения частиц дисперсной фазы по размерам, которая строится по экспериментальным данным.

В качестве статистических характеристик распределения частиц по размерам используются среднее значение, медиана и мода. Среднее значение – это некоторая средняя арифметическая величина, выражающая определенные характеристики. Существует несколько средних значений, которые могут применяться для характеристики размеров частиц. Медиана – это значение размера частиц, которое разделяет популяцию распределения точно на две равные части, т.е. точка на кривой, где 50% распределения находятся слева от этой точки, а 50% - справа. Модой, или модусом, называется такое значение размера частиц или класс распределения размеров, который в исследуемом распределении представлен в наибольшем количестве, т.е. это наивысшая точка кривой распределения.

Если распределение имеет нормальный характер по Гауссу, среднее значение, медиана и мода будут находиться в одной точке. В случае бимодального распределения значение среднего размера частиц будет соответствовать точке кривой, которая расположена точно между двумя распределениями. Частиц с такими размерами очень мало; они могут вообще отсутствовать в распределении. Мода – самая верхняя по оси Y точка кривой распределения, т.е. это частицы, которые представлены в данной системе в наибольшем количестве.

В приборах, основанных на гравитационной седиментации, частицы дисперсной фазы в результате оседания накапливаются в специальной кювете, где фиксируется вес осадка частиц. За время t вес осадка достигает постоянного значения, и оседание прекращается. Опытным путем определяют кривую седиментации. Зная H (путь оседания частиц) и время оседания t, находят скорость оседания v = H/t, а затем из закона Стокса – радиус частицы r:

(5.1)

где r – эквивалентный радиус частицы;

η – вязкость среды;

u – линейная скорость частицы;

D, d – плотность дисперсной фазы и дисперсной среды соответственно;

g – ускорение силы тяжести.

Кривая накопления осадка, или седиментационная кривая (рисунок 5.1) полидисперсной системы имеет начальный прямолинейный участок, который отвечает оседанию частиц всех размеров; он заканчивается при времени t_min , когда самые крупные частицы с радиусом r_max = K(H/t_min)^1/2 пройдут весь путь H от верха цилиндра до накопительной чашечки. После завершения оседания всех частиц вес осадка перестает изменяться; соответствующее время t_max позволяет определить радиус самых малых частиц r_min = K(H/t_max)^1/2.

Накопление осадка в процессе оседания частиц описывается уравнением Сведберга-Одена:

(5.2)

где P_i - общий вес осадка, накопившегося ко времени t_i;

q_i - вес частиц, полностью осевших к данному времени t_i, т.е. имеющих радиус больший, чем r_i = K(H/t_i)^1/2;

- скорость накопления осадка в момент времени t_i, которая определяется оседанием частиц с размером, меньшим r_i.

Это уравнение позволяет рассчитать фракционный состав дисперсной фазы посредством графического метода. Величина q_i численно равна отрезку, отсекаемому на оси ординат касательной, проведенной к седиментационной кривой в точке, соответствующей времени t_i.

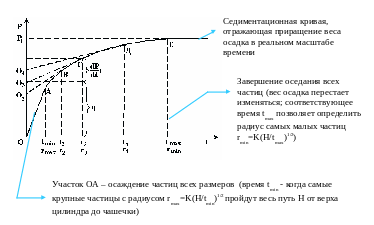
Рисунок 5.1 – Седиментационная кривая

Результаты седиментационного анализа представляют в виде зависимостей, отражающих распределение частиц по размерам. Кривая интегральной функции распределения (рисунок 5.2, а) изображает содержание (в % по весу) частиц с радиусами, большими данного r. Интегральная кривая обычно имеет S-образную форму с характерной точкой перегиба, соответствующей размеру частиц, весовая доля которых в данной дисперсной системе максимальна. С помощью интегральной кривой распределения частиц по размерам легко определить процентное содержание частиц с размерами, находящимися в заданном интервале от r_a до r_b: оно равно разности соответствующих ординат Q_a - Q_b.

Для построения интегральной кривой распределения на оси абсцисс откладывают значения радиусов в интервале r_min - r_max , а на оси ординат относительное содержание по весу частиц с радиусом от r_max до данного радиуса r_i, то есть частиц с радиусами, большими r_i.

Дифференциальная функция распределения (рисунок 5.2, б) дает более наглядное представление о фракционном составе суспензии. Для ее построения на интегральной кривой определяют значения Q для нескольких интервалов радиусов r и рассчитывают значения . Кривая распределения должна быть ограничена значениями r_min и r_max.

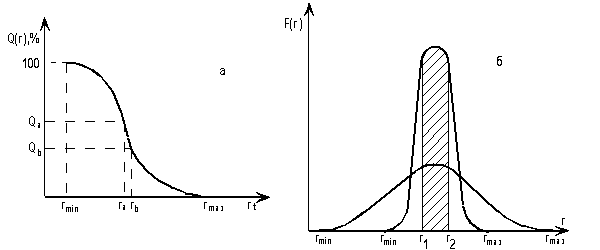
Рисунок 5.2 – Интегральная (а) и дифференциальная (б) функции

распределения

Используются также такие характеристики, как распределение количества частиц, объема частиц и поверхности частиц по размерам:

- доля количества частиц x_i, содержащихся в i-й фракции, от общего числа частиц в дисперсной системе определяется выражением

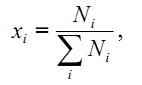
где N_i – количество частиц в i-й фракции;

- доля объема частиц i-й фракции определяется формулой

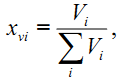
где V_i – суммарный объем всех частиц i-й фракции, м³;

- доля поверхности частиц i-й фракции определяется формулой

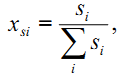
где s_i – поверхность частиц i-й фракции, м².

Среднеарифметический размер частиц равен

Среднеквадратическое отклонение размера частиц от среднего значения определяется выражением

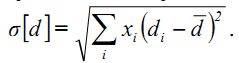
Дисперсия размера частиц равна

Отношение среднеквадратического отклонения размеров частиц к среднему значению называется коэффициентом вариации размеров частиц

Эта величина используется в качестве критерия различия между монодисперсными и полидисперсными системами. Если значение коэффициента вариации мало (например, 0,02), то разброс размеров мал по сравнению со средним значением, и систему можно считать монодисперсной. При больших значениях коэффициента вариации систему следует рассматривать как полидисперсную.

Еще одна характеристика дисперсности называется плотность распределения частиц по размерам и определяется выражением

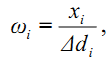
где Δd_i – разность между максимальным и минимальным размерами i-й фракции, м.

Помимо размеров частиц, важной характеристикой дисперсных систем является концентрация частиц дисперсной фазы. Концентрацией дисперсной системы называется количество частиц дисперсной фазы, содержащихся в единице объема системы.

Концентрация дисперсной системы определяется выражением

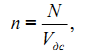
где N - количество частиц в дисперсной системе;

V_дс - объем дисперсной системы, м³.

Концентрация является удельной величиной и не зависит от объема дисперсной системы. Концентрация частиц также не зависит от размеров и формы

частиц, а определяется исключительно их количеством в единице объема.

Величиной концентрации определяются объем дисперсной системы, приходящийся на одну частицу

и среднее расстояние между дисперсными частицами

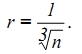
Если дисперсная система содержит частицы различных размеров, то частицам каждого размера соответствует своя концентрация

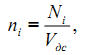
где N_i – количество частиц i-го размера в дисперсной системе.

Общая концентрация частиц дисперсной системы в этом случае равна

сумме концентраций частиц отдельных размеров

Общая концентрация и концентрация частиц отдельных размеров связаны выражением

В дисперсных системах каждая частица отделена от дисперсионной среды своей поверхностью контакта фаз. Полная поверхность контакта фаз в дисперсной системе определяется суммированием поверхностей всех частиц.

Для одной частицы сферической формы площадь межфазной поверхности равна

Для одной кубической частицы эта же площадь равна

Суммарная площадь частиц i-й фракции определяется выражением

Количество частиц i-й фракции можно вычислить через концентрацию частиц и объем дисперсной системы

Площадь поверхности контакта фаз дисперсной системы будет равна

Для частиц сферической формы это выражение примет вид

,

а для частиц кубической формы

В инженерных расчетах для упрощения вычислений полидисперсная система зачастую рассматривается как монодисперсная, по свойствам аналогичная полидисперсной. Такая замена правомерна, если монодисперсная система обладает той же поверхностью контакта фаз, что и полидисперсная.

Площадь межфазной поверхности в монодисперсной системе равна

где – диаметр частиц монодисперсной системы, м.

Приравнивая площади поверхности монодисперсной и полидисперсной систем, получаем

,

откуда диаметр частиц монодисперсной системы равен

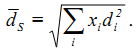
Указанный размер называется среднеповерхностным диаметром частиц полидисперсной системы.