2.2. Информация и неопределенность. Измерение неопределенности.

Статистический подход (Шеннон, Хартли, Колмогоров 20-40е года).

Количественно выраженная неопределенность состояния системы – энтропия. Получение информации связано с изменением степени осведомленности о состоянии системы Х:

I(X) = H(X) – H`(X),

где H(X) – степень неопределенности о состоянии системы до получения сообщения,

H`(X) – после сообщения.

При полном снятии неопределенности I(X) = H(X), когда, например, после получения сообщения однозначно стало ясно, что предприятие – банкрот.

Для системы с N равновероятными состояниями (например, N=2, когда рассматриваются два состояния «банкрот», «не банкрот») 

H(X) = K₀ log_aN,

где значение К₀, и «а» определяют систему измерения единиц информации.

Для системы с разновероятными дискретными состояниями: 

H(X) = -K0 åPi logaPi

Для системы с 2 равновероятными состояниями снятие неопределенности о состоянии системы дает одну единицу информации

1 = K₀ log_aN

Если принять К =1 и а=2, то правая часть = 1 Бит

В общем случае 

I = log₂N – формула Хартли, показывает сколько информации необходимо для снятия неопределенности о системе с равновероятными состояниями. Видно, что это зависит только от количества самих состояний.

При передаче кодированных сообщений из m символов в n разрядах (например, символы 0 и 1 в 16 разрядах) имеем I = n log2m . 

Для двоичного кода (0 и 1) количество информации в сообщении составит n двоичных единиц, которые называются битами.

Статистический подход не учитывает семантического и прагматического аспектов информации, применяется при оценки пропускной способности каналов передачи информации.

Семантический подход очень трудно формализуем, возможным путем является следующий.

Используется тезаурусная мера. Если есть тезаурус S потребителя – отражает знания его о данном предмете, то сообщение изменяет этот тезаурус

Количество смысловой информации I оценивается по степени изменения тезауруса.

А. Харкевич предложил измерять ценность информации через изменение вероятности достижения определённой цели, возникающее под воздействием данного сообщения. Семантическая информация (С.И.) в виде сообщения любой природы можно оценивать как степень изменения системы знаний (тезауруса) адресата в результате восприятия данного сообщения. Эта мера одновременно оценивает новизну и доступность сообщения относительно данного адресата, тем самым такая трактовка С. и. является в значительной мере прагматической (см. Прагматика). Отправитель сообщения тоже получает С. и., которая характеризуется возникшим у него новым знанием о состояниях тезаурусов адресатов.

I

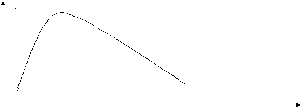
I

S opt S

  Рис.2.2. Зависимость количества смысловой информации от объема тезауруса потребителя

Интересно, что это изменение нелинейно зависит от объема тезауруса пользователя: при S=0 и I=0, но и при S≠0, I≠0

Этот метод показывает, что в семантическом смысле информация обладает свойством относительности и имеет субъективную ценность (рис. 2.2).

  Прагматический подход определяет количество информации как меру, способствующую достижению поставленной цели. Мера ценности информации – количество информации, необходимое для достижения цели. Подход базируется на теории Шеннона.

Прагматическое количество информации определяется: 

I = log2 P1/P0 [бит]

где P0, P1 – вероятность достижения цели до и после получения сообщения.

Структурный подход связан с задачами хранения информации.

Здесь абстрагируются от субъективной сущности и полезности информации. Используется только расчет количества символов и, по существу, занимаемый объем на диске. В данном подходе количество байтов – сколько имеет информация зависит от количества символов в сообщении. Естественно, это количество может не совпадать с количеством семантической или прагматической информацией.