16.Постановки задач

Задачі дослідження процесів функціонування ОС представлених послідовностями Маркова. Для стаціонарного режиму початкові умови системи не впливають на фінальні ймовірності (граничні). Задачі дослідження:1. Скласти балансні рівняння для заданого (самостійно) розміченого графу станів. Знайти фінальні ймовірності. Зважаючи на те, що кожен стан характеризується економічною оцінкою, обчислити М() для показника ефективності функціонування системи. M[E]=PiEi. Враховуючи, що матриці перехідних ймовірностей представляють стратегії впливу на поведінку системи, змінити елементи матриць і зробити 3 розрахунки. 2. Розв’язати задачу (1) для випадку, коли фінальна ймовірність деякого стану обмежена. max M[], SkS. 3. Розв’язати задачу (1) при умовах, що можуть змінюватись деякі рядки перехідної матриці.

17.Основные принципы им

Поняття про імітаційні моделі. Мета ІМ – відобразити динаміку(зміну в часі) процесів в системах і структурах з для аналізу характеристик функціонування. Особливості ІМ полягає у наступному: функціонування системи розглядається, як сукупність компонентів, що взаємодіють між собою. Компоненти системи синхронізовані за допомогою параметра. Особливість ІМ полягає в тому, щоб забезпечити використання моделей різних типів одночасно, наприклад дискретних та неперервних. Імітаційні моделі: а)Використання математичних моделей різних категорій; б)Система МК{вузли}; S={S_k(t)}_n в)Поведінка S_k(t); t – відображення динаміки; г)Взаємодія елементів: синхронізація, моделі системного часу; д)Використання випадкових величин із заданими законами розподілення; є)Евристичність, ситуативність, принцип спостереження, необхідність статистичної обробки і інтерпретація результату.

18.Методы ведения Моделювання часу в ІМ:

Властивості методів:Метод „До події” дозволяє спостерігати елементи в істині моменти часу. Він ефективний, коли події розподілені нечасто, нерівномірно, обробка кожної події потребує значного ресурсу. При цьому події, що виникають в різні моменти, враховуються окремо.При моделюванні „З заданим кроком” передбачається, що подій багато, вони досить рівномірні, обробка кожної події не потребує значного ресурсу, при цьому події в різні терміни можуть розглядатися, як одночасні. Події, близькі в фізичному часі, можуть бути рознесені.

19.Виды систем Одноканальна смо

Заявка Черга Канал

Багатоканальна СМО

λ – інтенсивність вхідного потоку заявок , ν – середній час обробки Модель СМО має наступні обмеження: Доступність каналів (заявка сама миттєво визначає вільний канал)

20. Марковские случ проц с дискр состоянием и непрер временем. уравн Колмогорова.Рівняння Колмогорова (аналог балансних рівнянь для систем ДСНЧ).

ый

Si

Визначити ймовірність, що в t+∆t система в Si.

Pi(t+∆t)-? Нехай A – подія, що в момент t+∆t система в стані Si.A=B(залишилась)+C(перейшла з інших станів) P(A)=Pi(t+∆t)(1) P(B)=(1-ij)∆t)Pi - умовна ймовірність (2) P(C)= ijPj∆t=Pij

При ∆t0 маємо похідну. Рівняння Колмогорова мають вигляд:

(**)

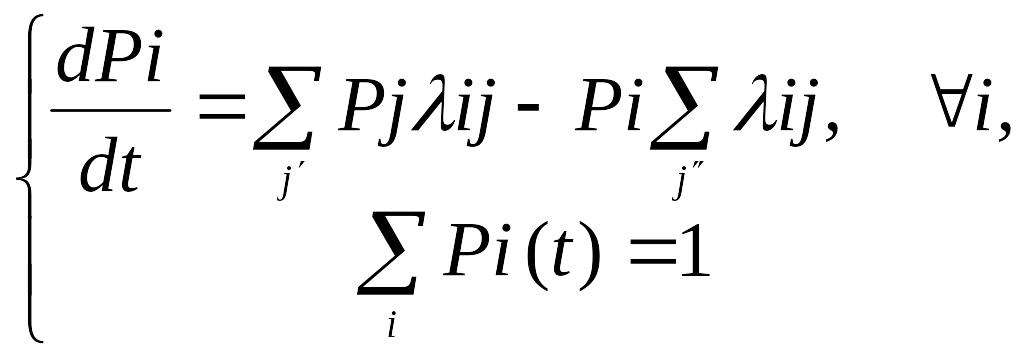Мнемонічне правило для (**):Потік ймовірностей для ДСНЧ систем: Piij.Складання рівнянь Колмогорова відбувається за схемою:

1) 2)Умова нормування Pi(t)=1, відкинути одне рівняння для Sij. Приклад: Скласти рівняння Колмогорова для системи.

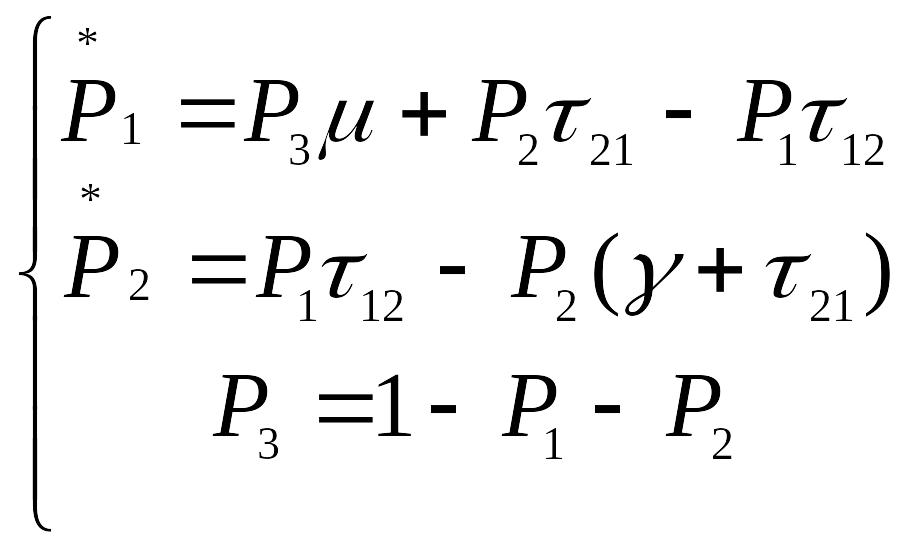P₁(0)=0.5; P₂(0)=0.5; P₃=0

21.Понятие ординарности Характеристики, властивості потоків подій. 1)Ординарність. Одночасно не може бути >1 подій.

2)Стаціонарність. Випадкова величина не залежить від моменту часу. ( t)= - інтенсивність.

3)Потоки без післядії (без пам’яті).