10.Модели потоков событий

1.Потік подій.

Q₁ Q2 Q₃ Q₄ Qi Q_i+1

t

Випадкові події:

- кількість елементів потоку на t;

- р(t, к_ел-тів).

Ti=Q_i+1-Q_i Різниця моментів між подіями. Види потоків визначаються властивостями Ti, а також залежністю або незалежністю окремих інтервалів. Види потоків: - Найпростіший потік (Пуассона); ▪ ординарний; ▪ стаціонарний; ▪ без пам’яті; - З обмеженою післядією (рекурентний) ; - Стаціонарний з обмеженою післядією (потоки Пальма) ; - Потоки Ерланга.

Потоки Пальма:

Пото ки Ерланга:

Регулярний потік:

Характеристики, властивості потоків подій.1) Ординарність. Одночасно не може бути >1 подій. 2)Стаціонарність.Випадкова величина не залежить від моменту часу.( t)= - інтенсивність.

1. Потоки без післядії (без пам’яті).

Матриці переходу(перехідних ймовірностей). Характеристики зміни станів:

Pij(t)=P(S(t)=Sj | S(t-1)=Si)

Однорідний процес ||Pij(t)||=||Pij|| (не залежить від часу). Для нього існує стаціонарний режим.

11.Вычисление вероятностейПоняття випадкового процесу з дискретним часом і станом. Функціонування обчислювальної системи як послідовність змін станів.

S(tk), k=0,1,2… S(Tk)=(S₁(Tk),S₂(Tk),…,S_m=4(Tk)). Головною задачею, що розв’язується при моделюванні – це ймовірність того, що S(Tk)=S_i, i[1,m].

12.Понятие случайной функ. Елементарні випадкові функції : звичайні функції часу, параметри яких є випадковими величинами

1. y1=a+bjt, bj є[b1,b2]

bj=b1+j(b2-b1), jє [0;1]

2. y2(t)=a +bt

3. y3=X Встановлено,що для моделі будь-якого випадкового процесу достатньо використати елементарні випадкові ф-ції.

13.Виды потоков событий Потоки подій при моделюванні обчислювальних систем та структур.

Властивості і види потоків. 1.Потік подій.

Q₁ Q2 Q₃ Q₄ Qi Q_i+1

T2=Q3-Q2

Випадкові події: - кількість елементів потоку на t; - р(t, к_ел-тів).

Ti=Q_i+1-Q_i Різниця моментів між подіями. Види потоків визначаються властивостями Ti, а також залежністю або незалежністю окремих інтервалів. Види потоків: - Найпростіший потік (Пуассона); ▪ ординарний; ▪ стаціонарний; ▪ без пам’яті;- З обмеженою післядією (рекурентний) ; - Стаціонарний з обмеженою післядією (потоки Пальма) ; - Потоки Ерланга.

Потоки Пальма:

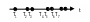
Потоки Ерланга:

Регулярний потік:

14.Марковские случайные Стаціонарний режим послідовностей Маркова: дсдч.

1. Моделювання функціонування системи. Система S(k)={Si(k)}_n, k=0,1,2,… Матриці переходів:

Pij(k) – ймовірності переходу із i-го в j-й стан на етапі k.

, стохастична матриця.

||Pij(k)||_n=||Pij||_n – послідовність однорідна.

Задача: Pi(k)-? Розрахувати ймовірність того, що на етапі k система в стані i.

Формула повної ймовірності:

Початкові умови: .

15.Условия стационарного. Умови існування стаціонарного режиму: (1) Однорідність: || Pij(k)||=||Pij|| (2) Ергодичність станів (зв’язаність).

Система може перейти з будь-якого стану до іншого безпосередньо або через інші стани. (3) Відсутність циклів.

Якщо система (1), (2), (3), то в системі існує стаціонарний режим (**).

3. Балансні рівняння стаціонарного режиму.

1). Розмічений граф станів системи.

2). Мнемонічне правило для балансних рівнянь. В стаціонарному режимі для кожного Si потік вхідних ймовірностей дорівнює потоку вихідних ймовірностей.

S1: P₃P₃₁+P₄P₄₁-P₁(P₁₂+P₁₃+P₁₄)=0

S2: P₁P₁₂-P₂(P₂₄+P₂₃)=0

S4: P₂P₂₄+P₁P₁₄-P₄(P₄₃+P₄₁)=0

P₁+P₂+P₃+P₄=0

PiPij – потік ймовірностей, Pi – невідомі в рівняннях.