Тема 3. Расчет плоских ферм

Как выбирается расчетная схема фермы?

За расчетную схему при узловой передаче нагрузки обычно принимается шарнирная ферма. Расчет, основанный на такой рас­четной схеме, является приближенным. Он не учитывает влияние жесткости соединений элементов фермы в узлах. Однако при узло­вой передаче нагрузки для многих ферм влияние жесткости узлов не слишком велико, поэтому указанная расчетная схема вполне приемлема.

Как связаны между собой значения продольных сил в поясах фер­мы и внутренних усилий в соответствующей балке?

Силы в поясах фермы N_п пропорциональны изгибающему мо­менту в соответствующей балке М^б: N_п = М^б / h, где h - высота фермы. Наибольший изгибающий момент возникает в средине пролета балки. Следовательно, в ферме постоянной высоты при та­кой же нагрузке наибольшие продольные силы возникают в сред­них стержнях фермы. При вертикальной нагрузке, направленной вниз, стержни верхнего пояса сжаты, нижнего - растянуты.

Как связаны между собой значения продольных сил в раскосах фермы и внутренних усилий в соответствующей балке?

Силы в раскосах фермы N_р пропорциональны поперечной силе в соответствующей балке Q^б: N_p = Q⁶/sin, где  - угол наклона раскоса. Нисходящие раскосы растянуты, восходящие сжаты.

Чем отличаются способы построения линий влияния в междуопорной и консольной части фермы?

Для стержней междуопорной части рассматривают равновесие левой части, если сила Р = 1 находится справа от сечения, и на­оборот - правой части, если сила слева. В этом случае в каждое уравнение входят только две силы - искомая N и одна из опор­ных реакций V.

Заметим, что можно составлять уравнения и по-другому, на­пример, для левой части, если сила слева. Линия влияния полу­чится такой же, но расчет будет сложнее.

Для стержней консольной части всегда рассматривают равно­весие отсеченной консоли. В этом случае в уравнения равновесия консоли входит не более двух сил - либо N и Р = 1, либо одна N.

Как определить положение передаточной прямой линии влияния продольной силы в стержне фермы?

Передаточная прямая (соединительная прямая, «срезка») на­ходится между узлами рассеченного стержня грузового пояса.

Как расположены левая и правая прямые линии влияния N в стержне пояса для фермы с параллельными поясами?

Левая и правая прямые пересекаются под моментной точкой.

Как расположены левая и правая прямые линии влияния N в рас­косе для фермы с параллельными поясами?

Левая и правая прямые параллельны.

ПРИМЕЧАНИЕ. Ответы можно (и даже нужно!) пояснять рисунками.

Тема 4. Расчет трехшарнирных систем

Что называется распорной системой?

Если вертикальная нагрузка, действующая на систему, вызывает в ее опорах наклонные реакции, такая система называется распорной. Нагрузка стремится раздвинуть опоры, как бы «распирает» их, отсюда и произошло название - «распорные системы». Горизонтальная составляющая опорной реакции называется распор.

Что называется трехшарнирной аркой?

Трехшарнирная арка - это распорная система, имеющая форму кривого стержня; она состоит из двух несущих дисков, со­единенных между собой и с землей шарнирами А, В, С.

Трехшарнирные арки статически определимы и геометрически неизменяемы.

Основные параметры трехшарнирной арки

Опоры А и В принято называть пятами, шарнир С замком арки, расстояние от прямой, соединяющей опоры, до замкового шарнира — стрелой подъема f, а расстояние между опора­ми по горизонтали - пролетом арки L.

Чем отличается трехшарнирная арка от трехшарнирной висячей системы?

Выпуклость арки противоположна действию нагрузки, в этом случае распор направлен внутрь арки.

Если выпуклость системы совпадает с направлением действия нагрузки, то распор будет направлен наружу. Такие системы носят название висячих.

Дать определение арки с затяжкой

Когда опорные устройства не способны воспринять распор, вво­дят дополнительный стержень (затяжку), соединяющий обе полуарки. Затяжка может быть расположена на уровне опор арки или выше их. Иногда затяжка выполняется ломаного очертания.

В расчетной схеме арки с затяжкой достаточно одной шарнирно-неподвижной опоры для обеспечения неподвижности системы в горизонтальном направлении; вторая опора принимается шарнирно-подвижной.

Опорные реакции в трехшарнирной арке в случае вертикальных нагрузок

Вертикальные составляющие R_A и R_В в опорах арки равны реакциям R_A^б и R_В^б в соответствующей балке:

.

Горизонтальные составляющие реакций (распор)

,

где – значение изгибающего момента в сечении С соответствующей балки (под шарниром С арки); f – стрела подъема арки.

Как зависят реакции в арке от стрелы подъема f, длины пролета l и очертания оси?

Вертикальные составляющие опорных реакций R_A, R_B зависят от длины пролета l и не зависят от стрелы подъема f и очертания оси.

Распор Н зависит от длины пролета l и стрелы подъема f, но не зависит от очертания оси. Распор тем больше, чем меньше стрела подъема и наоборот.

Внутренние усилия в арке

Изгибающий момент М, поперечная Q и продольная N сила в некотором сечении арки равны:

М = М^б - Ну; Q = Q^б cos - Н sin; N = - (Q^б sin + Н cos),

где у - ордината данного сечения;  - угол наклона касательной к оси арки в данном сечении; Н - распор арки; М^б , Q^б - изгибающий момент и поперечная сила в точке соответствующей балки с той же абсциссой, что и данное сечение.

Сравнить внутренние усилия в арке и балке одинакового про­лета

При одинаковом нагружении изгибающие моменты и попереч­ные силы в арке всегда меньше, чем в балке того же пролета (это следует из формул для их вычисления). В этом состоит одно из достоинств арок.

В арке, в отличие от балки, возникает продольная сила. Она сжимающая (N < 0), потому что, как правило, Q sin < Н cos.

Охарактеризовать эпюры внутренних усилий в арке

Эпюры внутренних усилий в арках всегда криволинейного очертания. Это видно из расчетных формул, в которых сомножителями слагаемых являются у, sin и cos, нелинейно изменяющиеся по длине пролета.

Из дифференциальной зависимости между моментами и поперечными силами следуют следующие правила: если на участке поперечная сила положительна (Q > 0), то изгибающий момент М на этом участке возрастает; при Q < 0 момент М убывает; если в некотором сечении Q = 0, то эпюра М имеет здесь экстремум.

Под сосредоточенной силой Р эпюра Q имеет скачок P sin, эпюра N – скачок P cos.

Опорные реакции в арке с затяжкой при вертикальной нагрузке

Вертикальная нагрузка вызывает в опорах только вертикальные реакции, горизонтальная составляющая реакции шарнирно­-неподвижной опоры отсутствует.

Вертикальные реакции опор равны реакциям соответствующей балки .

Затяжка АВ работает на центральное растяжение, в ней возникает только продольная сила N_зат, которая равна распору в обычной трехшарнирной арке без затяжки.

.

Внутренние усилия в арке с затяжкой

В трехшарнирной арке с затяжкой изгибающие моменты, поперечные и продольные силы определяются по формулам:

М = М^б - Ну; Q = Q^б cos - Н sin; N = - (Q^б sin + Н cos),

При этом усилие в затяжке N_зат играет роль распора Н: Н = N_зат.

Дифференциальная зависимость между моментами и поперечными силами в арке

Поперечная сила есть производная от изгибающего момента по длине оси арки: .

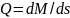Что такое рациональная ось арки?

Рациональной осью арки называется ось такого очертания, при которой размеры поперечного сечения будут наименьшими. Так как наибольшее влияние на прочность оказывают изгибающие моменты, то рациональной осью будет такая, при которой изгибающие моменты во всех сечениях арки равны нулю.

Уравнение рациональной оси

При действии на арку только вертикальной нагрузки уравнение рациональной оси

у (x) = М^б/Н.

Для фиксированной нагрузки распор Н является константой. Следовательно, рациональная ось по форме должна совпадать с очертанием эпюры изгибающих моментов М в соответствующей балке.

Если найдено такое очертание оси арки, при котором изгибаю­щие моменты во всех сечениях равны нулю (М = 0), то на основа­нии дифференциального соотношения поперечные силы во всех сечениях также равны нулю (Q = 0). Следовательно, в сечениях арки возникают только продольные силы N, т. е. арка работает исключительно на сжатие. Это особенно выгодно для каменных и бетонных сооружений.

Рациональная ось арки при действии равномерно распределенной нагрузки

Рациональная ось по форме совпадает с очертанием эпюры из­гибающих моментов М^б в соответствующей балке. При действии равномерно распределенной нагрузки эпюра М очерчена по квад­ратной параболе. Значит, рациональной осью арки является квад­ратная парабола.

Рациональная ось трехшарнирной системы при действии сосредоточенных сил

Рациональная ось по форме совпадает с очертанием эпюры из­гибающих моментов М^б в соответствующей балке. При действии сосредоточенных сил эпюра М^б имеет ломаное очертание. Значит, рациональной осью является ломаная линия. Это уже не арка, а трехшарнирная рама.

Рациональная ось арки при действии радиальной нагрузки (гидростатического давления)

Гидростатическое давление - это равномерно распределенная нагрузка, направленная по нормали к оси арки. Чаще всего такая нагрузка рассматривается при расчете арочных плотин.

Рациональное очертание оси трехшарнирной арки - дуга окружности.

Определение нормальных напряжений в арках

Арка представляет собой кривой стержень, поэтому при точном ее расчете надо учитывать кривизну. Применяемые в строительстве арки и своды в большинстве случаев пологие. Их допускается рассчитывать по приближенным формулам, т. е. считать, что напряженное состояние в сечении арки является та­ким же, как и в прямом, а не кривом стержне.

Нормальные напряжения при внецентренном сжатии определяются следующим образом:

где М - изгибающий момент; N - продольная сила; А - площадь поперечного сечения; J - момент инерции сечения относительно главной оси инерции, перпендикулярной плоскости изгиба.

Как не допустить появление растягивающих напряжений в сечении арки?

Для арок, выполненных из хрупкого материала (кирпич, бетон), нежелательно появление растягивающих напряжений. Поэтому для таких арок кривая давления не должна выходить за пределы ядра сечения.

(Кривая давления - это линия действия внутренней силы, передающейся вдоль арки).

Линии влияния опорных реакций в арке

Вертикальные составляющие реакций R_A и R_B определим из уравнений моментов относительно центров опор.

Линии влияния внутренних усилий в арке (способ наложения)

Пусть сечение К имеет координаты Z_K, У_K и угол наклона . Линии влияния изгибающего момента M_K, поперечной Q_K и продольной N_K сил в этом сечении строятся на основании их общих выражений:

.

Это значит, что линии влияния М_K, Q_k, N_k можно получить, построив линии влияния 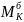, и Н, умножив их на соответствующие коэффициенты, а затем сложив ординаты. Прямые, огра­ничивающие линии влияния, носят названия: левая прямая - от опоры А до сечения К, средняя прямая - от сечения К до шарнира С, правая прямая - от шарнира С до опоры В.

Расчетное положение нагрузки на арке

Прочность материала арок проверяется по нормальным напряжениям в крайних точках поперечных сечений. Можно раздельно рассматривать линии влияния N_K и M_K и исследовать несколько положений нагрузки на арке. Порядок расчета следующий:

1. определяется расчетное положение нагрузки по положительной части л. в. M_K; вычисляется значение момента и соответствующее ему значение продольной силы ;

2. определяется расчетное положение нагрузки по отрицательной части л. в. М_K вычисляется значение момента и соответствующее ему значение продольной силы ;

3. определяется расчетное положение нагрузки по л. в. N_K; вычисляется значение продольной силы и соответствующее ему значение момента ;

4. при каждом из этих трех положений определяются нормальные напряжения в крайних точках сечения и из них выбираются численно наибольшие для каждого знака.

Данный метод является приближенным, так как линии влияния изгибающего момента и продольной силы отличаются по своей форме, и расчетные положения нагрузки для них различны.