2.9. Памятка программисту

Выводы, полученные в настоящей главе, можно свести в краткий перечень рекомендаций для практической орга­низации вычислений. Некоторые упражнения, приведенные в конце главы, иллюстрируют эти рекомендации; на эти упражнения даны ссылки.

1. Если необходимо произвести сложение—вычитание длинной последовательности чисел, работайте сначала с наименьшими числами (упражнение 13).

2. Если возможно, избегайте вычитания двух почти равных чисел. Формулы, содержащие такое вычитание, часто можно преобразовать так, чтобы избежать подобной операции (упражнения 12, 14 и 18).

3. Выражение вида a(b — с) можно написать в виде аЬ—ас, а выражение вида (Ь—с)/а можно написать в виде b/a — с/а. Если числа в разности почти равны друг другу, производите вычитание до умножения или деления. При этом задача не будет осложнена дополнительными ошибками округления (упражнения 16 и 17).

4. В любом случае сводите к минимуму число необходи­мых арифметических операций

( упражнения 6 и 7).

Упражнения

*1. Ток протекает по резистору 10 ом, известному с точностью ± 10%. Ток равен 2 ± 0.1 а. Согласно закону Ома, падение напряжения на резисторе равно произведению тока на сопротивле­ние. Каковы относительная и абсолютная ошибки вычисленного зна­чения напряжения? Ошибками округления пренебречь.

2 . Средняя длина авиалинии от Нью-Йорка до Сан-Франциско равняется 2700 милям, но может быть на 200 миль короче или длин­нее в результате вариаций маршрута самолета. Средняя скорость самолета на этой линии составляет 580 миль в час, но может оказать­ся на 60 миль в час больше или меньше из-за ветра. Каковы верхний и нижний пределы времени полета?

3. Реактивное сопротивление емкости дается формулой

где Xс— реактивное сопротивление емкости в омах,

f—частота в герцах, С—емкость в фарадах.

Указать границы возможных значений Хс для f = 400 ± 1 гц и С = 10 ^-7 ф ± 10%.

4 . Положение S свободно падающего тела в вакууме дается следующей формулой:

где g — ускорение свободного падения в м/сек², t—время, прошедшее с начала падения, в сек..

Предположим, что g= 9.81 м/сек². точно, но время может быть изме­рено только с точностью до 0.1 сек. Покажите, что с ростом t абсолют­ная ошибка вычисленного значения S увеличивается, но относи­тельная ошибка уменьшается.

*5. Предположим, что а есть положительное, соответствующим образом округленное число и что число 2 можно записать в ЭЦВМ точно. Начертите графы вычислительных процессов и выведите формулы для максимально возможных относительных ошибок при вычислении и = а + а и v = 2a. Покажите, что эти ошибки оди­наковы.

*6. При тех же предположениях, что и в упражнении 5, пока­жите, что максимально возможная относительная ошибка для u=а + а + а больше, чем для u =3а. Проиллюстрируйте этот вывод на примере а = 0.6992, сохраняя после каждой арифмети­ческой операции четыре десятичные значащие цифры.

7. Предположим, что а и Ь являются положительными и соот­ветствующим образом округленными числами. Начертите графы вычислительных процессов и выведите выражения для максимально возможных ошибок при вычислении u = ( а + а+ а ) b и v=3(ab). Покажите, что максимально возможная относительная ошибка больше для первого выражения. Проиллюстрируйте для а = 0.4299 и b= 0.6824.

*8. Предположим, что х есть соответствующим образом округ­ленное число. Нарисуйте графы вычислительных процессов, выведи­те выражения для максимально возможных ошибок и покажите, что границы ошибок одинаковы для

и =(х²)² и v=x*(x*(x*x)).

9. При тех же предположениях, что и в предыдущем упражне­нии, начертите графы вычислительных процессов, выведите выраже­ния для максимально возможных ошибок и покажите, что ошибки одинаковы для

и=х*(х*(х*(х*(х*(х*(х*х)))))) и для v = ((x²)²)².

10. Покажите, что если пользоваться десятичной арифметикой с конечным количеством значащих цифр, то 10./10.= = 10. * (1./10.) и 2./2.=2. * (1./2.), но 3./3.  3.* (1./3.)

*11. Предположим, что а, Ь и х положительны и заданы точно. Начертите графы вычислительных процессов, выведите выражения для максимально возможных ошибок и покажите, что для и = ах + Ьх² и v=x (а+ bx) пределы ошибок одинаковы. В качестве численного примера возьмите а = 0.7625, b==0.6947 и х= 0.4302. Покажите, что хотя максимально возможные ошибки и одинаковы, но действительные ошибки, будучи меньше максимально возмож­ных, вовсе не обязаны быть одинаковыми.

12.Предположим, что а и Ь положительны, заданы точно и что а > Ь. Покажите, что хотя и справедливо равенство (а+ Ь) = (а² — Ь²)/(а — Ь) (при вычислениях с бесконечно большой точ­ностью), тем не менее в результате ошибок округления вычисленные значения левой и правой частей выражения могут сильно разли­чаться. Покажите, что наихудший случай имеет место тогда, когда ошибки округления при вычислении а² и Ь² максимальны, но имеют противоположные знаки. Проиллюстрируйте на примере a = 0.3525 и Ь = 0.3411, используя десятичную арифметику с четырьмя зна­чащими цифрами.

13. Предположим, что а есть соответствующим образом округ­ленное положительное число и что 1 можно представить в ЭЦВМ точно. Рассмотрим выражения u = (1 + а)² и v=1 + (2а+а²). Покажите, что при а >> 1 максимально возможные относительные ошибки для и и v почти равны, но при а << 1 максимально возможная относительная ошибка для и почти в 3 раза больше, чем для v. Проиллюстрируйте это для а = 0.2635.

14. Начертите граф вычислительного процесса и выведите выражения для максимально возможных относительных ошибок при вычислении (а + Ь) — Ь. Проиллюстрируйте для a = 0.8614*10^-2 и b = 0.9949, а также для а = 0.3204 и

Ь = 0.5837.

15. Рассмотрим выражение 5а + b.Покажите, что при вычисле­нии этого выражения относительная ошибка величины а скажется в пять раз сильнее, чем относительная ошибка величины Ь.

*16. Рассмотрим выражения и=(а—Ь)/с и v=a/c—Ыс. Предположим, что а, Ь и с положительны и заданы точно и что a  Ь. Покажите, что относительная ошибка округления для v может быть гораздо больше, чем для и. Проиллюстрируйте для а=0.41, b=0.36 и с=0.70. Используйте десятичную арифметику с двумя значащими цифрами.

17. Рассмотрим выражения а (Ь—с)=и и аЬ—ас=v. Предположим, что а, Ь и с все положительны; кроме того, Ь > с и Ь  с. Покажите, что при этих условиях и имеет гораздо меньшую максимально возможную относительную ошибку. Покажите, что для а=0.9364, b=0.6392 и с=0.6375 значение u=0.1592*10^-2, вычисленное с четырьмя значащими цифрами, равно соот­ветствующим образом округленному точному ответу, в то время как v=0.1500*10^-2.

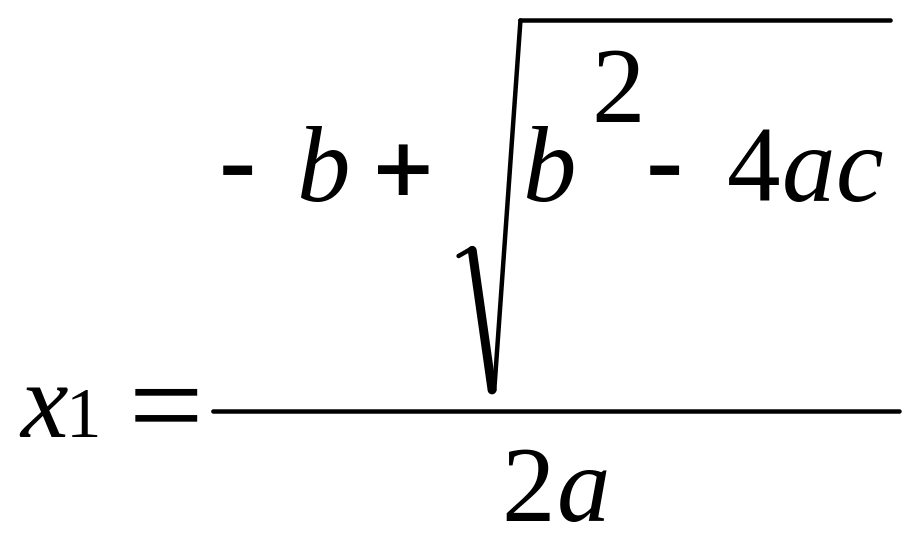* 18. Дано квадратное уравнение ах²+Ьх+с=0; предпо­ложим, что все коэффициенты положительны, заданы точно и что Ь²>> 4ас. Сначала покажите, что при вычислениях с бесконечным количеством значащих цифр меньший из двух корней может быть вычислен по любой из формул:

или

Теперь покажите, что при заданных ограничениях на коэффициенты вторая формула обеспечит гораздо более высокую точность. Покажите, что для а=0.1000*10¹, b= 0.4002*10° и c=0.8000*l0^-4 x₁= 0.1500*10^-3 и x^’/₁= 0.2000*10^-3. Последняя вели­чина равна точному значению корня. (Операцию извлечения квад­ратного корня можно представить на графе в виде кружка, к кото­рому ведет стрелка только от одной величины. Относительная ошибка исходной величины появляется в квадратном корне умно­женной на 0.5, и этот коэффициент можно поставить около стрелки. При извлечении квадратного корня появляется также дополнительная ошибка округления, которая в большинстве трансляторов ФОРТРАН не превосходит 10^-t+1.)

19. Рассмотрим систему уравнений

ax+by=c,

dx+ey=f

и их решение по правилу Крамера

Покажите, что если ae — bd мало по абсолютной величине, то точность решения может оказаться низкой, даже если все коэффи­циенты заданы точно. Проиллюстрируйте на примеое системы уравнений:

0.2038x + 0.1218y = 0.2014

0.4071x+ 0.2436y = 0.4038

Решение этой системы, полученное при вычислениях с четырьмя значащими цифрами, равно х = —1.714 и y = 4.286, в то время как точное решение, полученное при вычислениях с восемью зна­чащими цифрами, равно х = —2.000 и y = 5.000. Если коэффици­енты уравнений сами содержат ошибки, как это почти всегда и быва­ет, то «решение» этой системы может оказаться полностью бессмыс­ленным.

ГЛАВА

5