8.6. Итерационные методы решения систем линейных уравнений

В разд. 8.2 мы рассмотрели метод исключения (конеч­ный метод), с помощью которого можно решить систему линейных алгебраических уравнений. Затем в разд. 8.4 мы увидели, как можно уточнить решение, повторно ис­пользуя метод исключения. В сущности, этот метод уточ­нения решения является итерационным. Таким образом, и здесь проявляется обычное противоречие между теорией и практикой вычислений на ЭЦВМ — благодаря ошибкам округления решение, получаемое с помощью конечного и точного метода, может сильно отличаться от истинного,c помощью же итерационного метода это решение можно существенно улучшить.

В этом разделе мы рассмотрим другой, более обыч­ный итерационный метод, отличающийся простотой и лег­костью программирования. Подобно итерационным мето­дам из гл. 5, он отличается малой ошибкой округления, но в то же время сходится только при выполнении некоторых условий, которые мы также рассмотрим.

Оказывается, что условия сходимости этого итерацион­ного метода очень часто выполняются тогда, когда с помо­щью определенных приемов решаются уравнения в частных производных. К этому вопросу мы ещё вернемся в гл. 11 . Рассмотрим систему из трех уравнений с тремя неиз­вестными (8.5), (8.6) и (8.7). Предположим, что a11<>0,a22<>0,a33<>0, и перепишем систему в следующем виде:

x1 = 1/a11*(c1 - a12x2 - a13x3), (8.32)

x2 = 1/a22*(c2 - a22x2 - a23x3), (8.33)

x3 = 1/a33*(c3 - a32x2 - a33x3), (8.34)

Теперь возьмем некоторое первое приближение к ре­шению этой системы, обозначив его через x1^0,x2^0,x3^0. Под­ставим это решение в (8.32) и вычислим новое значение x1:

x1^(1) = 1/a11*(c1 - a12x2^0 - a13x3^0),

Используя только что вычисленное значение x1^(1) и на­чальное значение x3^0 вычислим из уравнения (8.33) новое значение x2:

x2^(1) = 1/a22*(c2 - a21x1^1 - a23x3^0),

Наконец, используя только что вычисленные значения x1^(1) и x2^(1), найдем из (8.34) новое значение x3:

x3^(1) = 1/a33*(c3 - a31x1^1 - a32x2^1) .

Этим заканчивается первая итерация. Теперь мож­но заменить исходные значения x1^0,x2^0,x3^0 на x1^1,x2^1,x3^1 и вычислить следующее приближение. В общем случае k-ое приближение определяется формулами

x1^(k) = 1/a11*(c1 - a12x2^(k-1) - a13x3^(k-1))

x2^(k) = 1/a22*(c2 - a21x1^(k) - a23x3^(k-1)) (8.35)

x3^(k) = 1/a33*(c3 - a31x1^(k) - a32x2^(k)) .

Заметим, что текущие значения неизвестных сразу же используются для последующих вычислений и что, напри­мер, нельзя вычислять x2^(k), пока не получено x1^(k). Ана­логично этому для вычисления x3^(k) необходимо сначала определить x1^(k) и x2^(k).

Только что описанный здесь метод известен как ите­рационный метод Гаусса — Зейделя. Этот метод исклю­чительно удобен для использования на ЭЦВМ. Перед обоб­щением на случай n уравнений с n неизвестными и выво­дом условия сходимости метода рассмотрим простой чис­ленный пример

4õ1 - x2+x3 = 4,

x1+6x2+2x3 = 9,

-x1 -2x2+5x3 = 2 .

Нетрудно убедиться, что точное решение этой системы равно x1 = 1, x2= 1, x3= 1. Положим x1^0=x2^0=x3^0=0 , как это обычно делается для начального приближе­ния. Тогда, вычисляя согласно формулам

x1=1/4*(4+x2-x3) ,

x2=1/6*(9-x1-2x3),

x3=1/5*(2+x1+2x2),

получаем следующее приближение:

x1^(1) = 1

x2^(1) = 4/3

x3^(1) = 17/15 .

Последовательные приближения, вычисленные каждый раз с точностью до четырех значащих цифр, приведены в табл. 8.1. Таблица 8.1

Итерация	x1	x2	x3
0	0	0	0
1	0.1000*10^1	0.1333*10^1	0.1133*10
2	0.1050*10^1	0.9473*10^0	0.9889*1
3	0.9896*10°	0.1005*10^1	0.9999*1
4	0.1001*10^1	0.9999*10^0	0.1000*10
5	0.1000*10^1	0.1000*10^1	0.1000*10

Интересно отметить, что вычисления с восемью знача­щими цифрами приводят к такой же точности снова за пять итераций. Однако следующие четыре итерации дают уже решение с точностью до восьми значащих цифр.

Рассмотрим теперь систему (8.13) из n уравнений с n не­известными. Мы по-прежнему предполагаем, что диаго­нальные коэффициенты aij отличны от нуля для всех t. Тогда k-e приближение к решению будет задаваться фор­мулой

xi^(k) = 1/aii*(ci - ai1x1^(k) - ... - ai,i-1xi-1^(k) - ai,i+1xi+1^(k-1) - ...

... - ainxn^(k-1)) , i = 1,2, ... ,n .

Итерационный процесс продолжается до тех пор, пока все xi^(k) не станут достаточно близки к xi^(k-1). Критерий близости можно, например, задать в следующем виде:

M^(k) = max I xi^(k) - xi^(k-1) I <  ,

где определяется максимальное значение разности для всех i, а  - некоторое положительное число. При выпол­нении критерия итерационный процесс следует остановить. Можно заменить этот критерий близости, сравнивая с  не абсолютные, а относительные разноcти

max I (xi^(k) - xi^(k-1))/ xi^(k) I <  .

Блок-схема программы для вычислений по методу Га­усса — Зейделя приведена на рис. 8.9. Она вовсе не так сложна, как это может показаться с первого взгляда. Вспомним хотя бы, что блок-схема для метода исключения заняла три рисунка — 8.5, 8.6 и 8.8.

В левой части рисунка изображены действия, связан­ные со вводом исходных данных и подготовкой к вычисле­ниям. В этой части рисунка указано, что начальное при­ближение принимается равным нулю, а счетчику количества итераций присваивается значение 1. Как обычно, для подсчета количества итераций используется целая пере­менная ITER. При дальнейших вычислениях эти началь­ные действия не повторяются. В конце этой части блок-схемы стоит кружок с цифрой внутри, так называемая связка. Эта связка означает, что блок-схема продолжается, начиная с кружка, содержащего ту же цифру, в нашем слу­чае со средней части рисунка, где вверху поставлен кру­жок с цифрой 1. Связки часто используются в блок-схемах, чтобы не проводить длинных пересекающихся линий.

Переменная BIG используется для того, чтобы опреде­лять наибольшее значение разности между xi^(k) и xi^(k-1). Сначала этой переменной присваивается значение нуль, а затем с ней сравниваются абсолютные значения разностей Ixi^(k) - xi^(k-1)I. Если какая-либо разность оказывается по абсолютной величине больше BIG, то прежнее значение BIG заменяется этой разностью. После вычисления всех xi^(k) наибольшая разность будет равна значению перемен­ной BIG.

Затем в блок-схеме следует группа действий, с помо­щью которых вычисляется сумма всех членов уравнения, кроме диагонального. По ходу программы удобнее сначала вычислять и суммировать члены, стоящие перед диагональ­ным (так как в них используются новые значения xi^(k) ), а уже потом — члены, идущие после него (так как в них используются старые значения xi^(k-1) ). Необходимо также несколько усложнить эту логику в связи с тем, что в пер­вом и последнем уравнениях отсутствуют члены, стоящие соответственно до и после диагонального.

В правой части блок-схемы указана группа действий, начинающаяся с вычисления нового значения xi^(k) ; опреде-

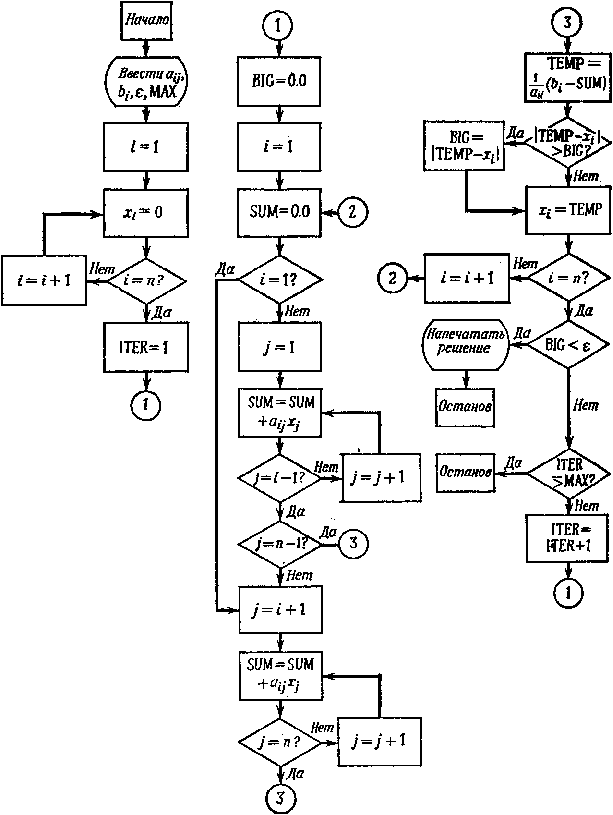
Р и с. 8.9. Блок-схема программы для решения системы линейных уравнений итерационным методом Гаусса — Зейделя.

ляется максимальная разность и запоминается новое зна­чение xi^(k). Если это было не последнее уравнение, то мы увеличиваем индекс i и начинаем вычислять очередное приближение для следующего неизвестного. В случае по­следнего уравнения мы сравниваем максимальную разность с  и печатаем результаты, если процесс сошелся. Если же итерационный процесс не сошелся, то мы производим опе­рации, относящиеся к самому программированию, но не к численному методу. Дело в том, что процесс, который должен сходиться, в действительности не всегда сходится. Причин этому может быть очень много: от ошибок в про­грамме до неверных исходных данных. Поэтому в начале программы с перфокарты было прочитано целое число МАХ, которое определяет максимально допустимое число итера­ций. Обычно это число выбирается несколько большим необходимого количества итераций. (Ориентировочно для МАХ можно принять значение 50 при решении системы из 50 уравнений.) Тогда, если по какой-либо причине ите­рационный процесс не сошелся, ЭЦВМ не будет работать бесконечно долго. Практически для любого итерационного метода

работать бесконечно долго. Практически для любого итерационного метода необходимо предусматривать в программе такой счетчик в той или иной форме.

В блок-схеме указано, что исходная информация вво­дится в машину извне и результаты печатаются. Заметим, что на практике исходные данные для системы уравнений часто вычисляются самой же ЭЦВМ в некоторой пред­шествующей программе, а результаты столь же часто используются для последующих вычислений. Пример ис­пользования результатов вычислений в последующей прог­рамме мы рассмотрим в разд. 8.8 (практический при­мер 10).

Теперь обратимся к вопросу сходимости метода. Перед обобщением на случай n уравнений подробно рассмотрим более простой пример -- систему из двух уравнений. За­пишем уравнения в виде

a11x + a12y = c1 , (8.36)

a21x +a22y = c2 , (8.37)

так что

x^(k) = 1/a11*(c1 - a12y^(k-1)) , (8.38)

y^(k) = 1/a22*(c2 - a21x^(k)) . (8.39)

Если обозначить

dx^(k) = x - x^(k) ,

dy^(k) = y - y^(k) ,

то из (8.36) и (8.38) следует

dx^(k) = - a12/a11*dy^(k-1) ,

а из (8.37) и (8.39)

dy^(k) = - a21/a22*dx^(k)

Сравнивая последние два уравнения, нетрудно получить, что

dy^(k) = (a12a21)/(a11a22)*dy^(k-1) .

Аналогично

dy^(k-1) = (a12a21)/(a11a22)*dy^(k-2) ,

так что

dy^(k) = ((a12a21)/(a11a22))^2*dy^(k-2) .

Продолжая дальше таким же образом, получим

dy^(k) = ((a12a21)/(a11a22))^(k)*dy^(0) .

Аналогично

dx^(k) = ((a12a21)/(a11a22))^(k)*dx^(0) .

Поэтому если I (a12a21)/(a11a22) I < 1 (8.40)

то итерационный метод Гаусса — Зейделя сходится к реше­нию уравнений (8.36) и (8.37) .

Нетрудно увидеть аналогию между выкладками, произведенными в этом разделе, и теми, которые были использованы при решении вопроса о сходимости метода после­довательных приближений в разд. 5.2. Соотношение (8.40) можно удовлетворить, если

I a11 I > I a12 I (8.41)

I a22 I >= I a21 I

или если

I a11 I >= I a12 I (8.42)

I a22 I > I a21 I

Иными словами, диагональные члены должны преобла­дать в уравнении, т. е. они должны быть по абсолютной

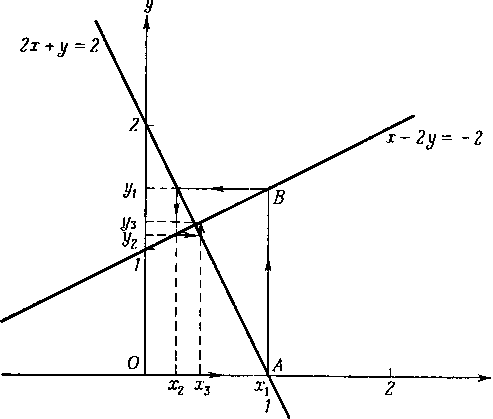
Рис. 8.10. Геометрическое представление итерационного метода Гаусса — Зейделя для случая сходимости.

величине не меньше, а по крайней мере в одном случае больше недиагональных членов. Рассмотрим простой пример

2x + y = 2 ,

x - 2y = - 2 .

Точное решение равно x = 2/5, y = 6/5 , как показано на рис. 8.10. Результаты последовательных

итераций составляют

Итерация	x	y
0	0	0
1	1	3/2
2	1/4	9/8
3	7/16	39/32

Полезно представить себе процесс решения геометриче­ски. Мы начинаем искать решение от начала координат (0, 0). Так как при вычислении x мы сохраняем неизмен­ным значение y, то геометрически это соответствует дви­жению по горизонтали до пересечения ее с прямой, соот­ветствующей первому уравнению (2х + y = 2). Затем, со­храняя неизменным только что найденное значение x, мы начинаем двигаться по вертикали, пока не пересечем прямую, соответствующую второму уравнению (x - 2y = - 2). На рис. 8.10 такому процессу соответствует путь

OAB. На этом заканчивается одна итерация.

Дальнейшие итерации производятся точно таким же образом; на рис. 8.10 их последовательность представлена горизонтальными и вертикальными линиями со стрелками. Заметим, что процесс сходится к решению системы урав­нений. Отметим также сходство между рис. 8.10 и рис. 5.2. Посмотрим теперь, что случится, если мы переставим уравнения:

x^(k) = - 2 + 2y^(k-1) ,

y^(k) = 2 - 2x^(k) .

Результаты последовательных итераций составляют

Итерация	x	y
0	0	0
1	- 2	6
2	10	- 18
3	- 33	78

Геометрически этот случай проиллюстрирован на рис. 8.11. Снова можно отметить сходство с рис. 5.4. Труд­ность на этот раз состоит в том, что угол наклона прямой, соответствующей первому уравнению, меньше 1 и поэто­му Ах получается чересчур большим. Аналогично, боль­шой угол наклона прямой, соответствующей второму урав­нению, приводит к слишком большой величине &у. Ко­роче говоря, процесс расходится. Очевидно, что для сходимости процесса первая прямая

^

Рис. 8.11. Геометрическое представление итерационного метода Гаусса —

Зейделя для случая расходимости.

должна иметь наклон больше 1, а вторая — меньше 1. Эти условия полностью эквивалентны условиям (8.41) и (8.42), записанным в аналитическом виде.

Вспомним, однако, что фактически условие сходимо­сти, которому нужно удовлетворить, выражается форму­лой (8.40) и что это условие гораздо слабее условий (8.41) и (8.42). Зададимся вопросом: возможен ли случай, когда первая прямая имеет наклон меньше 1, но вторая имеет такой малый угол наклона, что процесс тем не менее схо­дится? Или, иными словами, если даже dх велико, то может ли dy быть достаточно малым, чтобы обеспечить сходимость метода? На этот вопрос можно ответить положительно. Рассмотрим следующий пример:

x + 2y = 3 ,

x - 4y = - 3.

Наклон прямых, соответствующий обоим уравнения меньше 1. Поэтому

I a11 I < I a12 I ,

т. е. нарушено и условие (8.41), и (8.42). Заметим, однако что условие (8.40) для этой системы удовлетворяется

Рис. 8.12. Геометрическое представление итерационного метод Гаусса — Зейделя для случая, когда достаточные условия сходи мости не выполнены, но метод тем не менее сходится.

Геометрическое толкование процесса последовательных приближений показано на рис. 8.12. Результаты последователь­ных итераций составляют

Итерация	x	y
0	0	0
1	3	3/2
2	0	3/4
3	3/2	9/8
4	3/4	15/16

Решением этой системы являются x = 1, y = 1.

Таким образом, условия (8.41) и (8.42) являются до­статочными условиями для сходимости, но они не являют­ся необходимыми. Иными словами, выполнение какого-нибудь из них гарантирует сходимость метода, но в то же время существуют системы, для которых эти условия не выполняются, но метод итераций все равно сходится.

Мы рассмотрели пример, где наклон первой прямой был меньше -1,а второй -положителен, но меньше +1, т. е.

k1 < - 1 ,

0 < k2 < + 1 .

Как показывает рис. 8.10, сходимость носила в этом случае колебательный характер.

В другом примере, где наклоны удовлетворяли нера­венствам

0 < k1 < 1 ,

k2 < - 1 .

расходимость также являлась колебательной.

Можно легко проверить, что при I k1I >= 1, Ik2I <= 1, где по крайней мере одно из неравенств является строгим, справедливы следующие утверждения:

1. Если k1 и k2 имеют одинаковые знаки, то процесс сходится к решению с одной стороны.

2. Если k1 и k2 имеют разные знаки, то сходимость носит колебательный характер.

Теперь мы приведем без доказательства достаточные условия сходимости итерационного метода Гаусса — Зейделя для системы из n уравнений с n неизвестными. Если система уравнений неприводима ^), если

I aii I >= I ai1 I + ... + I ai,i-1 I + I ai,i+1I + ... + I ain I

для всех i и если по крайней мере для одного i

I aii I > I ai1 I + ... + I ai,i-1 I + I ai,i+1I + ... + I ain I

^ Система уравнений называется неприводимой, если нельзя вычислить какие-либо неизвестные, решая меньше чем n уравнений.

то итерационный метод Гаусса — Зейделя сходится к реше­нию системы уравнений (8.13).

Выполнение этих условий обеспечивает сходимость метода. Мы еще раз подчеркиваем, что эти условия ни в коем случае не являются необходимыми. Они выведены путем соответствующего обобщения условий (8.41) и (8.42).

У читателя может возникнуть вопрос, оставляют ли эти достаточно жесткие условия какую-либо практическую возможность для применения метода Гаусса — Зейделя. Оказывается, что да. Во многих областях прикладной ма­тематики возникает необходимость решать системы линей­ных уравнений, причем коэффициенты этих уравнений по­лучаются такими, что условия сходимости метода Гаус­са — Зейделя автоматически выполняются. В частности, именно такими получаются системы, связанные с решением на ЭЦВМ уравнений в частных производных, как мы это увидим в гл. II.

Наконец, отметим следующее: по аналогии с резуль­татами гл. 5 следует ожидать, что увеличение очередных поправок (экстраполяция) или их уменьшение (интерполя­ция) может ускорить сходимость метода. В действитель- ности дело именно так и обстоит. Окончательное обсуж-j дение этого вопроса мы откладываем до гл. II.