
- •Прямі та ітераційні методи розв’язування різницевих рівнянь
- •Розглянемо модельну задачу
- •Застосування методів Якобі і Зейделя для розв’язування систем різницевих рівнянь.
- •Метод Зейделя
- •Метод верхньої релаксації для модельної задачі
- •Ітераційний метод з Чебишевським набором параметрів
- •Застосування Чебишевського методу до модельної задачі
- •Застосування Чебишевського методу до рівнянь еліптичного типу зі змінними коефіцієнтами
- •Позмінно–трикутний метод
- •Застосування позмінно-трикутного методу до модельної задачі
- •Позмінно-трикутний метод з Чебишевським набором параметрів
- •Ітераційний метод змінних напрямків
- •Застосування методу до модельної задачі
- •Метод колокацій
- •Метод найменших квадратів.
- •Метод Гальоркіна
Метод колокацій
Розглянемо рівняння
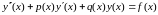 (1)
(1)
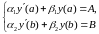 (2)
(2)
 ,
,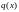 ,
,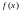 - задані функції з потрібними
диф.властивостями ( тобто мають другі
похідні ), і є непевні на [a,b]
;
- задані функції з потрібними
диф.властивостями ( тобто мають другі
похідні ), і є непевні на [a,b]
;
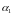 ,
,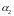 ,
,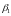 ,
,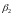 ,
,
,
,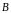 - відомі
- відомі
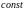 ,
,
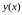 -
шукана функція. Як правило на ці константи
накладаються умови
-
шукана функція. Як правило на ці константи
накладаються умови
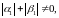
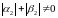
Побудуємо
систему функцій
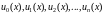 (3),
що задовольняють умовам :
(3),
що задовольняють умовам :
ця система функцій є лінійно незалежною ;
ця система функцій є повною – за допомогою цієї системи можна наблизити з довільною стелінню точності функцію з цього класу :
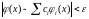
ця система функцій має на [a,b] неперервні похідні до другого порядку включно
функція
 задовольняє неоднорідним крайовим
умовам :
задовольняє неоднорідним крайовим
умовам :
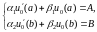 (4)
(4)
а
функції
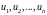 задовольняють крайовим умовам :
задовольняють крайовим умовам :
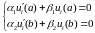 (5)
(5)
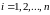 .
.
Будемо
шукати розв’язок (1),(2)
у вигляді
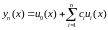 (6)
(6)
де
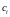 ,
, - невідомі коефіцієнти. Очевидно, що (6)
задовольняють умовам (2)
при довільних значеннях коефіцієнтів.
Підставимо (6)
в (1).
Отримаємо :
- невідомі коефіцієнти. Очевидно, що (6)
задовольняють умовам (2)
при довільних значеннях коефіцієнтів.
Підставимо (6)
в (1).
Отримаємо :
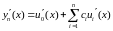 (7)
(7)
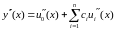 (8)
(8)
Підставимо (7), (8) в (1). Одержимо нев’язку :
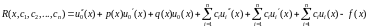 Якби
нам вдалось так підібрати
Якби
нам вдалось так підібрати
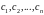 ,
що
,
що
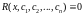 ,
то (6)
було б розв’язком (1),(2)
, бо задовольняє граничні умови і основне
рівняння. Але так вдається зробити дуже
рідко, то вимагають, щоб
,
то (6)
було б розв’язком (1),(2)
, бо задовольняє граничні умови і основне
рівняння. Але так вдається зробити дуже
рідко, то вимагають, щоб
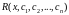 перетворювався в нуль в досить густій
системі точок ( точки колокацій ) і тому
виберемо систему точок
перетворювався в нуль в досить густій
системі точок ( точки колокацій ) і тому
виберемо систему точок
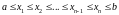 і будемо вимагати, щоб
і будемо вимагати, щоб
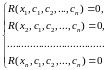 (9)
(9)
(9)
– це
система лінійних алгебраїчних рівнянь
відносно
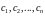 .
Якщо система має розв’язок, то знайшовши
ми
маємо наближений розв’язок (6)
задачі (1),(2).
Зрозуміло, що чим більше
.
Якщо система має розв’язок, то знайшовши
ми
маємо наближений розв’язок (6)
задачі (1),(2).
Зрозуміло, що чим більше
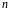 ,
тим точніший розв’язок.
,
тим точніший розв’язок.
Приклад 1:
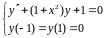
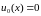 ,
бо крайові умови однорідні. Виберемо
базисні функції
,
бо крайові умови однорідні. Виберемо
базисні функції
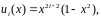
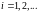 які
задовольняють крайовим умовам. Тоді
розв’язок :
які
задовольняють крайовим умовам. Тоді
розв’язок :
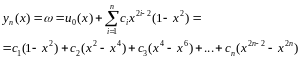
Обмежимось
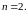 За точки колокації візьмемо
За точки колокації візьмемо
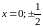 .
.
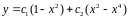
Підставимо в початкове диф.рівняння :
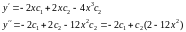
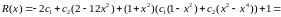
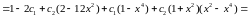
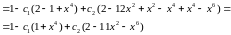
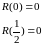
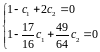
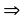
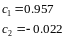
Маємо
наближений розв’язок :
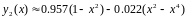
При
 :
:
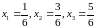
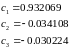
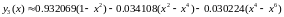
Приклад 2 :
Розв’яжемо задачу про усталений розподіл температури у стержні нескінченої довжини.
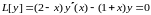 (10)
(10)
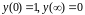 (11)
(11)
Розв’язок
будемо шукати у виді :
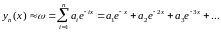
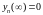 -
виконується
-
виконується
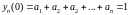 -
виконується.
-
виконується.
Знайдемо нев’язку при :

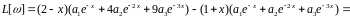
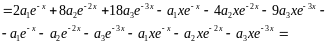
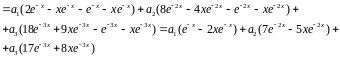
Метод колокацій викликав у строгих математиків сумніви до недавнього часу :
цілком очевидний його зв’язок із інтерполяцією, а відомо, що процес інтерполяції у загальному випадку не є рівномірно збіжним ;
не зрозуміло, як вибирати точки колокацій, і як від цього буде залежати розв’язок ;
для двохвимірних (і більших розмірностей) задач не маємо гарантії, що вибрані точки не належать кривій якогось порядку 1-го, 2-го і т. д. і у нас не вийде система рівнянь, що має розв’язок.
Метод найменших квадратів.
Проілюструємо цей метод на такій задачі :
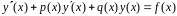 (1)
(1)
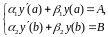 (2)
(2)
Виберемо
систему функцій
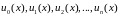 так, щоб
так, щоб
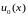 задовольняла неоднорідні умови :
задовольняла неоднорідні умови :
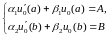 (3)
(3)
а
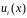 - однорідні граничні умови :
- однорідні граничні умови :
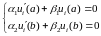 (4)
(4)
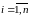 .
.
Наближений розв’язок задачі (1),(2) будемо шукати у виді :
 (5)
(5)
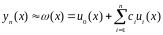
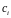 -
шукані коефіцієнти.
-
шукані коефіцієнти.
Функція (5) задовольняє умови (2) при будь-яких значеннях невідомих коефіцієнтів.
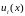 -
двічі неперервно диференційовні функції
на
-
двічі неперервно диференційовні функції
на
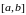 ,
лінійно незалежні ;
,
лінійно незалежні ;
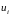 - базисні функції або координатні
функції. Знайдемо
- базисні функції або координатні
функції. Знайдемо
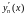 і
і
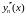 і
підставимо в (1).
Отримаємо нев’язку
і
підставимо в (1).
Отримаємо нев’язку
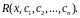
У методі найменших квадратів вимагається, щоб
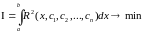
За змінними . Необхідною умовою мінімуму є :
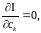
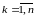 (7)
(7)
 (8)
(8)
Розв’язавши систему рівнянь (8), ми знайдемо коефіцієнти . Знайдемо розв’язок (5) задачі (1),(2). Система (8) є лінійною і її можна розв’язати будь-яким відомим методом.
Необхідні
умови в даному випадку є достатніми,
тому що
 >0.
>0.
Приклад :
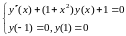

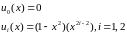
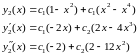
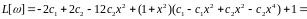
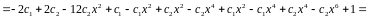
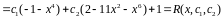
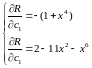
Підставимо в (8) і знаходимо інтеграли :
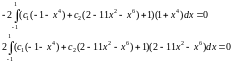
Одержимо систему :
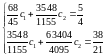
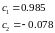
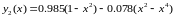
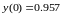 -
метод колокацій
-
метод колокацій
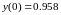 -
метод найменших квадратів
-
метод найменших квадратів
