Застосування методу до модельної задачі

Розглянемо модельну задачу

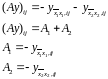
Таким чином, метод змінних напрямків для даної задачі буде виглядати так :

(17) (18)

де ,

Рівняння (17) розв’язується при кожному фіксованому , за допомогою методу прогонки по напрямку . Для цього (17) можемо записати у виді :

де 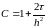і застосувати формули прогонки.

Так само рівняння (18) записуємо у виді :

При кожному фіксованому розв’язуємо методом прогонки по напрямку .

Число ітерацій. Необхідних для досягнення заданої точності , в даному випадку буде рівно

Порядок такий же як і в позмінно-трикутному методі.

Методи , що базуються на мінімізації нев’язки

Існує багато методів розв’язування крайових задач відмінних від методу сіток. Ці методи побудовані на зовсім іншому принципі. Цей принцип полягає в апроксимації шуканого розв’язку за допомогою функцій, які залежать від параметрів. При цьому числові значення параметрів вибираються із умови мінімізації деякої визначеної величини або функціоналу. Нехай задане деяке диференціальне рівняння :

(1)

В області і задовольняють умови (2) :

(2)

, - оператори крайових умов, - границя області , в якій задано основне диф. рівняння.

Розглянемо деяку функцію від змінних, яка залежить від параметрів

і можуть співпадати і не співпадати. і цілі числа.

Нехай ця функція задовольняє умовам

де - оператори крайових умов, - границя області , в якій задано основне диф. рівняння. Ці умови повинні задовольнятись при довільних значеннях параметрів ,при чому, їх кількість може не співпадати з розмірністю простору.

Підставимо цю функцію в основне диференціальне рівняння :

(3)

Ми одержали деяку величину, відмінну від нуля, яку називається нев’язкою. Якби параметри були такими, що функція , то було б розв’язком задачі, бо задовольняється і основне рівняння і граничні умови. Але так підібрати параметри вдається дуже рідко, чи дуже важко. Методи, які мінімізують нев’язку завиваються прямими або варіаційними.

Є інший підхід до розв’язування задач математичної фізики. Будується система функцій, яка задовольняє основне рівняння, при будь-якому наборі параметрів, а потім ці параметри підбираються так, щоб задовольнялися граничні і початкові умови.

Приклад: - аналітична функція, тоді її дійсна і уявна частини є гармонічними функціями, тобто вони задовольняють рівняння Лапласа :

Функція 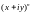- аналітична, бо розкладається в абсолютно-збіжний степеневий ряд. Візьмемо :

- рівняння Лапласа.

- Коші-Рімана.

Цей напрямок методів відомий як методи Трефтуа. Методи дозволяють звести задачу математичної фізики безпосередньо до системи алгебраїчних рівнянь.

Методи мінімізації нев’язки відносяться до так званих прямих методів розв’язання задач математичної фізики. Вони дозволяють звести задачу математичної фізики (1),(2) до алгебраїчної задачі з порівняно невеликою кількістю параметрів. Зокрема такими методами є варіаційні методи, які спочатку зводять задачу (1),(2) до задачі на екстремум, а потім цю задачу зводять до алгебраїчної задачі.

Варіаційні методи мають свою перевагу над різницевими методами, саме, вони не є такі чутливі до розмірності задачі. Але мають і свої недоліки :

1. Дуже важко побудувати функцію , яка б задовольнила всі граничні умови і мала необхідні властивості ;

2. Матриця системи, з якої визначаються параметри є густо заповненою, що вимагає застосування загальних методів розв’язання систем ( метод Гауса );

3. Зі збільшенням параметрів обумовленість системи погіршується.

Функція, яка задовольняє всім граничним умовам (2) і має необхідні диф.властивості та враховує апріорну інформацію про задачу називається структурою розв’язку. В останні роки ( десятиліття ) ця теорія розвинулась харківськими математиками під керівництвом В.Л. Рвачова та його учнями.

Частинним випадком прямих методів є так звані варіаційні методи, що зводять задачу математичної фізики до мінімізації деякого функціоналу.

Зараз вважається, що двомірні задачі вигідно розв’язувати методом сіток, а трьохмірні та вищих розмірностей – варіаційними.

Конкуренція цих методів породила метод скінчених елементів, який погасив недоліки і одних і других. Проілюструємо ідеї цих методів на прикладі простих задач.