Застосування Чебишевського методу до модельної задачі

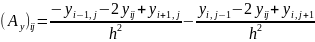
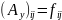
Для даної модельної задачі ми знаємо мінімальне та максимальне власне значення

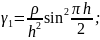
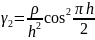
Із (19) маємо

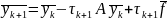
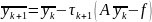
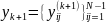
Спочатку по відомим 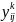вираховуємо нев’язку

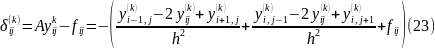
Далі дораховуємо значення 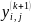за формулою

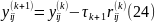i,j=1,2,3...N-1

При цьому покладаємо

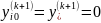
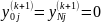i,j =1,2,…N-1

Швидкість збіжності ітераційного методу визначається параметром

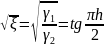
Оскільки крок є невеликий, то можемо рахувати що

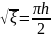
Можемо оцінити число ітерацій n, які потрібно виконати, для зменшення початкової похибки в раз.

де

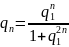
Досить вимагати щоб ,

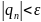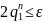
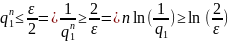
Тобто для того щоб початкова похибка зменшилась в раз досить вибрати

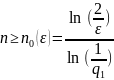
Вираховуємо

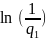
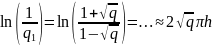
(25)

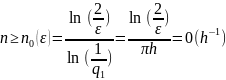
Для методу верхньої релаксації

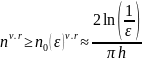розглянемо

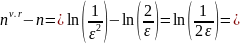
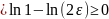
Метод верхньої релаксації вимагає більше операцій 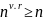. метод з чебишевським набором параметрів є оптимальним, але він вимагає певного впорядкування параметрів

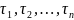
Якщо взяти 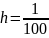,то метод Якобі вимагає 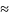10 тис. ітерацій ( 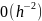), метод Зейделя 50 тис. ітерацій, метод верхньої релаксації 100 ітерацій при умові що ми оптимальним чином вибрали параметр

Метод Чебишева вимагає ще менше ітерацій, при умові що ми знаємо мінімальне та максимальне власне значення що буває дуже рідко. Якщо ми їх не знаємо, то можемо оцінити оператор А таким чином

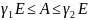
І чим ближчі до мін і макс власних значень, тим кращі оцінки і тим менша кількість ітерацій, які потрібно виконати.

Застосування Чебишевського методу до рівнянь еліптичного типу зі змінними коефіцієнтами

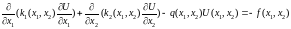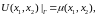
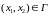(1)в обл. . (2) 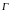- границя області .

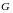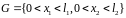
Припустимо, що 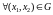виконуються нерівності :

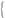(3)

(4)

Розіб’ємо область такими прямими :

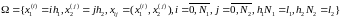
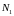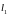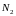- кількість розбиття прямокутника по стороні ;

- кількість розбиття прямокутника по стороні ;

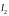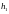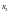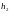- крок по осі ; - крок по осі ;

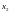Для апроксимації похідних використаємо такий прийом :

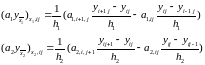(5)

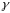- сіткова границя .

Виберемо 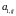і 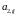таким чином, щоб виконувались умови апроксимації 2-го порядку

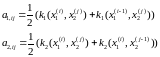(6)

В результаті підстановок (5) і (6) замість відповідних похідних ми одержимо різницеву задачу

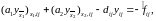
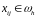(7)

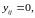
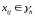(8)

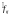- означає, що ми від неоднорідної задачі перейшли до однорідної – стандартним прийомом «загнавши» неоднорідні граничні умови в праву частину рівняння. Якщо введемо оператор

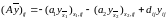(9)

І ввести простір сіткових функцій, що обертаються в нуль на границі області , то нашу задачу можна записати у виді операторного рівняння

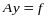(10)

- самоспряжений і додатньовизначений оператор . В просторі сіткових функцій визначений скалярний добуток і норма :

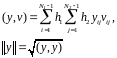(11)

Для рівняння (10) можна одержати такі оцінки :

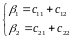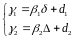(12) (13) (14)

Маючи 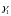та 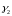можемо обчислити ітераційні параметр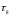и також обчислюємо величину похибки. Після того, як параметри знайдені ітерації проводимо для схеми :

,

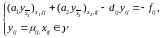
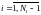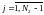
Спочатку обчислимо нев’язку :

,

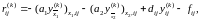Потім знаходимо нове наближення :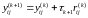

Граничні умови довизначаються згідно .
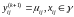