Метод Зейделя

Згідно методу Зейделя ітерації виражаються так

Тобто для індексів >i береться знач. на попередніх ітераціях, а для індексів 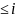з даної ітерації

Тоді , (12)

, . ,

Покладемо в (12) і=1, j=1 n=0 і знач що потрапляє на границю .

Визначимо 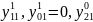задане задане

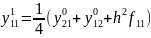
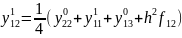
Таким чином невідомі визначаються в наступному порядку зміни індексів (1,1)(1,2)…(1,N-1),(2,1)(2,2)…(2,N-1)….(N-1,1)(N-1,2)…(N-1,N-1)

В цьому випадку говорять, що обчислення ведуться від лівого нижнього кута прямокутника до правого верхнього кута прямокутника.

Г рафічно можемо зобразити наступним чином

Метод Зейделя збігається швидше методу Якобі .

Але порядок збіжності такий, же як і в методі Якобі . Для того щоб поч. похибку зменшити в раз потрібно виконати ітерацій.

Швидшим на порядок є метод верхньої релаксації.

Метод верхньої релаксації для модельної задачі

Розглянемо застосування методу верхньої релаксації до модельної задачі (4)

Метод верхньої релаксації можна записати так

(13) n=0,1,….. – задане

Перепишемо (13) у виді:

(14)

Перепишемо рівність (4) у вигляді:

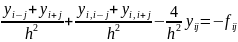, (15)

Із (15) видно що перша частина суми відповідає матриці А1, а друга А2, третя матриці D. Згідно (14) (15) метод верхньої релаксації запишеться так

(16)

Перепишемо (16) у виді:

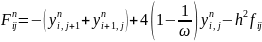
Обчислення починаємо з лівого верхнього кута області G

в рівняння (17) підставимо i=1 j=1 і визначимо і так далі

( i=1, j=2)(1,3)…(1,n)(2,1)….

Можемо довести що метод верхньої релаксації є збіжним, і для оптимального вибору параметрів для модельної задачі

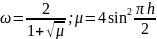
Кількість ітерацій які треба виконати, для того щоб поч. похибка зменшилась в раз

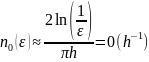
Знайти оптимальне значення параметру вдається тільки для простих задач, тому велика кількість досліджень присвячена вивченню того як зміниться кількість ітерацій якщо параметр буде близьким до оптимального

Ітераційний метод з Чебишевським набором параметрів

Будемо розглядати систему 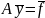(18)

Де А- додатньовизначена, симетрична матриця

Припустимо, що для А виконані матричні нерівності

E- одинична матриця

За можемо взяти відповідно найменше і найбільше власні значення

матриці А. Але в більшості випадків вони не відомі. Тому за беруть нижню додатню границю власних значень, а за верхню границю власних значень. Для розв’язання системи (18) використаємо явний нестаціонарний метод Річардсона

Де k- номер ітерації, - заданий початковий вектор

які в цьому випадку будемо вибирати чебишевським методом

вибираються таким чином щоб при заданому числі ітерацій n мінімізувати похибку середньоквадратична норма.

В цьому методі параметри вибираються так

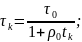
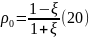
; k=1,2,3…,n

Якщо вибрати згідно попередніх формул то для похибки буде справедлива наступна оцінка

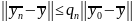(21) ; ; (22)

Таким чином щоб застосувати чебишевський метод до конкретних систем потрібно:

1. ВПЕВНИТИСЬ В ТОМУ ЩО МАТРИЦЯ А СИМЕТРИЧНА або довести, що матриця А відповідає самоспряженому оператору

2. Знайти границі спектру матриці А.

3. Обчислити параметри за формулами (20) і впорядкувати їх так щоб забезпечити стійкість методу.