Розглянемо модельну задачу

(Задача Діріхле для рівняння Пуассона)

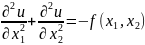(3)

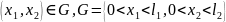з границею Г

Введемо в розгляд сітку

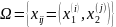
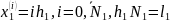
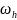- множина внутрішніх точок

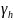- множина граничних точок

Тоді 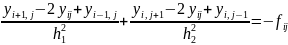(4)

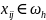
(5)

Покажемо, що система (4)(5) має такі особливості:

1. Для 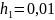(що дуже часто зустрічається в практичних задачах) система має великий порядок 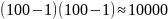, але якщо її записати у вигляді

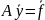(6) то матриця системи є сильно розріджена, в кожному рядку цієї матриці не більше 5 елементів відмінних від нуля.

2. Обумовленість системи погіршується із зменшенням 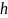. Від системи (4)(5) потрібно перейти до системи (6) наступним чином: перейменувати змінні в залежності від того як ми перенумеруємо змінні, та одержимо той чи інший метод, який відрізняється ефективністю

Нехай 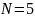Перейдемо від двовимірного масиву до одновимірного

Перехід здійснюється за формулою

Для того, щоб знати який вигляд має матриця А підставимо в систему рівнянь (4)

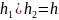
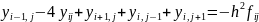
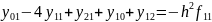
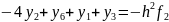
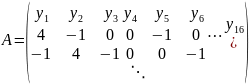
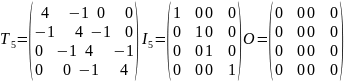Тоді А можна записати у вигляді

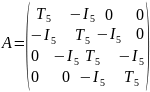
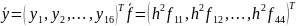
Матриця системи (6) є розрідженою і має стрічкову структуру.

Існують також інші методи перенумерації вузлів. І від тої чи іншої перенумерації залежить ефктивність методу.

В багатьох випадках записувати систему у виді (6) не є обовязковим.

Застосування методів Якобі і Зейделя для розв’язування систем різницевих рівнянь.

Запишемо різницеве рівняння Пуассона (4) в операторній формі 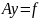де оператор А визначений наступним чином

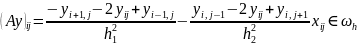
Нагадаємо деякі поняття і означення з теорії ітераційних методів. Однокрокові ітераційні методи можемо записати наступним чином

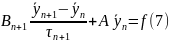
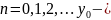заданий вектор

невироджені вибрані матриці

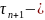параметр, який використовують для прискорення та забезпечення умов збіжності

Якщо 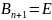то методи називаються явними

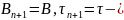стаціонарні методи частинним випадком (7) є

1. метод простої ітерації ? ? ?

2. Метод Річардсона

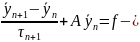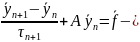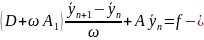3. метод верхньої релаксації, де

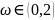
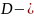діагональна матриця, 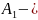нижня трикутна матриця.

В методі Якобі система рівнянь 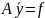має вигляд

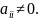
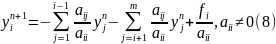
Згідно методу Якобі визначимо ітерації для рівняння (4) при умові , 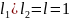наступним чином

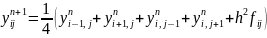(9)

задані числа початкові наближення

Покажемо, що метод Якобі збігається повільно, і співпадає з методом простої ітерації при оптимальному виборі значення ітераційного параметра.

При цьому має місце наступна теорема.

Теорема: Якщо матриця А – симетрична і додатньовизначена, то метод простої ітерації збігається при

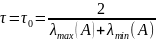
При чому швидкість збіжності є найбільшою, і мають місце нерівності

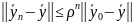
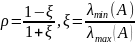
Запишемо метод простої ітерації для системи різницевих рівнянь

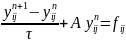
(10)

Для різницевого оператора Лапласа маємо

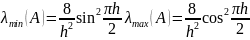
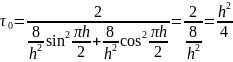
Підставимо в (10) це значення і зробимо спрощення то одержимо рівність (9)

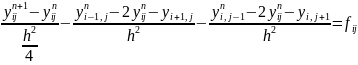
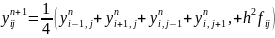
Метод простої ітерації (10) з параметром співпадає з методом Якобі (9)

Поскільки метод простої ітерації є збіжним, то метод Якобі також є збіжним.

Швидкість збіжності визначається параметром 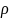. Для того, щоб зменшити початкову похибку в 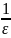раз треба, щоб виконувалась нерівність

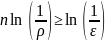
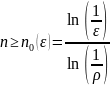кількість ітерацій, яку необхідно виконати для зменшення початкової похибки раз

=

=

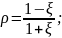
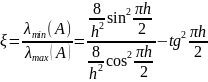
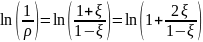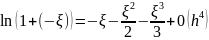
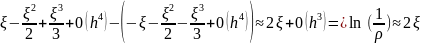
При

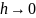
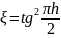
Тоді (11)

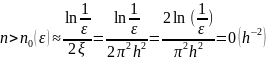
Звідси бачимо що метод збігається, але швидкість збіжності є повільна.

Якщо взяти h=1/100, то щоб забезпечити не дуже високу точність 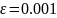то ми одержимо таку кількість ітерацій 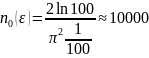ітерацій Є методи які вимагають лише 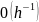ітерацій або