Прямі та ітераційні методи розв’язування різницевих рівнянь

Якщо потрібно розв’язати задачу математичної фізики

(1)

В області G, де L – диференціальний оператор, де f(x) відома функція, U(x) – шукана функція де G – деяка m вимірна замкнена область то найчастіше використовують метод сіток.

Вважаємо, що початкові та граничні умови враховані оператором L та правою частиною f(x).

Згідно методу сіток від задачі (1) переходимо до задачі (2)

(2)

в області (2) представляє собою розширену задачу.

Перехід від (1) до (2) можна здійснювати різними методами

1. За допомогою формул чисельного диференціювання, коли змінюємо похідні їх різницевими аналогами Розглянемо приклад (бігармонійний оператор)

Якщо замінити похідні їхніми різницевими аналогами то одержимо

Розглянемо рівняння задане по такому шаблоні (13-точковий шаблон)

Ми замінили похідні їх різницевими аналогами на основі формул чисельного диференційювання, так щоб похибка апроксимації була порядку .

2. Другий спосіб побудови системи різницевих рівнянь є інтегро-інтерполяційний метод.

Від (1) до (2) переходять так, щоб зберігав усі основні властивості головного оператора (симетричність, додатньовизначеність), та властивості самої задачі(рівняння теплового балансу, закони Кіргофа в задачах електростатистики). Такі схеми які це враховують наз. консервативними(їх побудова є досить складною задачею).

3. Варіаційними методами – методом скінченних елементів.

4. Метод невизначених коефіціентів

При переході від (1) до (2) виникають такі проблеми

1. Існування розвязку системи (2) та його єдиність(Ці проблеми для багатьох задач можна вирішити на основі принципу максимуму).

2. Питання апроксимації. Чи буде ?

3. Коректність, стійкість(чи буде розвязок задачі (2) стійким при зміні параметрів) та збіжність. Питання апроксимації та стійкості вирішуються відносно легко, а питання збіжності є важким. Але якщо диференціальна задача поставлена коректно і різницева схема є коректною то з апроксимації випливає збіжність.

4. При розв’язуванні різницевих задач виникають проблеми пов’язані з вибором методів розвязаних.

Система (2) має особливості і одна з них це велика кількість рівнянь. Кількість невідомих = кількості внутрішніх вузлів.

При розв’язуванні різницевої задачі (2) виникають проблеми:

1. Який метод вибирати і який є ефективнішим;

2. Якими мають бути параметри методів (зокрема в методі верхньої релаксації ).

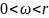Як правило вибір таких оптимальних значень параметра звязаний з власними значеннями, або їх оцінками. Але ці значення відомі для небагатьох задач і тоді виникає задача: наскільки зміниться швидкість збіжності, якщо ми обрали неоптимальне значення, а близьке до нього.

В багатьох сучасних методах використовується апостеріорна інформація про одержані результати і на основі неї вносяться корективи у параметри.

3. Майже всі методи є ітераційними, або поєднуються з прямими (є гібридними методами) тому постає питання про умову закінчення ітераційного процесу

Покажемо, що система рівнянь (2) має такі властивості:

1. Велика кількість рівнянь

2. Розрідженість матриці системи

3. Погіршення обумовленості з ростом кількості рівнянь.

Розглянемо задачу – рівняння теплопровідності

Якщо задача однорідна : то вона легко розв’язується, бо існує ефективний алгоритм розвязування відповідної різницевої задачі – метод прогонки.

Якщо ж задача двомірна, то хоча і існує метод матричної прогонки, але він не є такий ефективний, і використовується для областей, які мають видовжену форму в напрямку однієї змінної.

Якщо ж задача трьох мірна, то розв’язання ще більше ускладнюється.

Якщо візьмемо

Тоді кількість рівнянь буде рівна

Виникає ефект «прокляття розмірності»

Припустимо, що розв’язуємо систему методом Гауса, який вимагає операцій. Таким чином дана задача не розвяжеться.

Нащастя такі системи мають позитивну характеристику – розрідженість мариці. Наприклад, якщо беремо 5-ти точковий шаблон то матриця системи для відповідної модельної задачі має в кожному рядку не більше 5-ти елементів , якщо брати 9-ти точковий шаблон то в кожному рядку буде не більше 9-ти елементів , при 13-ти точковому шаблоні не більше 13-ти елементів .

При чому сучасні методи орієнтовані на врахування структури матриці.