4.8.3 Составление уравнения гиперболы по координатам ее фокусов (расстоянию между фокусами) и эксцентриситету
Задача 35 Составить уравнения
гиперболы, фокусы которой лежат на оси
ох, расстояние между фокусами равно 6,
а эксцентриситет
.
Решение
1 Т.к.фокусы гиперболы ,то а –действительная ось и уравнение гиперболы имеет вид:
.
2 Найдем полуфокальное расстояние:
по условию задачи
3 Найдем действительную полуось:
по условию
,
воспользуемся определением эксцентриситета
.
Имеем:
подставив в полученное равенство
значение с, получим:
4 Найдем длину мнимой полуоси по формуле:
5 Подставим a и b в уравнение гиперболы, получим:
Задача 36 Составить уравнение гиперболы, фокусы которой находятся в точках F1(0;-5), F2(0;5), а эксцентриситет
Решение
1 Т.к.фокусы гиперболы
,то
b –действительная ось и уравнение
гиперболы имеет вид:
.
2 Найдем полуфокальное расстояние:
по условию задачи F1(0;-5),
F2(0;5),тогда
3 Найдем действительную полуось:
по условию
,
воспользуемся определением эксцентриситета
.
Имеем:
подставив в полученное равенство
значение с, получим:
4 Найдем длину мнимой полуоси по формуле:
5 Подставим a и b в уравнение гиперболы, получим:
4.8 Уравнение гиперболы со смещенным центром (смещенная гипербола)
4.8.1 Связь общего уравнения кривых второго порядка с общим уравнением гиперболы
Рассмотрим общее уравнение (2) линий второго порядка, т. е. уравнение
Если в общем уравнении кривых второго
порядка (2) произведение коэффициентов
А и С отрицательное, причем
,
то оно определяет гиперболу.
или
,
- гипербола.
4.8.2 Расположение гиперболы в декартовой системе координат в зависимости от коэффициентов d и e
Если в уравнение (2)
то
уравнение
определяет гиперболу с центром в начале координат, и сводиться к каноническим уравнениям:
,
.
Если в уравнении (2)
и
,
то его можно привести с помощью выделения
полного квадрата относительно х
и у к виду
или
,
где
- центр гиперболы.
Г
ипербола,
которая определяется уравнением (3)
строиться с помощью параллельного
переноса осей координат в точку
и построения в новой системе координат
эллипса
или
,
где
,
.
Рассмотрим возможные случаи
4.8.1 
,
(
)
,
(
)
,
(
)
,
(
)
Если
в уравнении (2)
Е=0, то уравнение
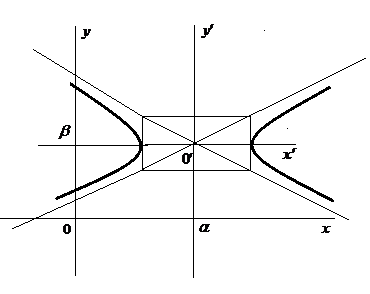
Определят гиперболу смещенную вдоль оси Ох и его можно привести к каноническому виду
или
(2.3)
где
.
Рассмотрим возможные случаи
(
)
(
)
Если в уравнении (2) D=0,
,
то уравнение
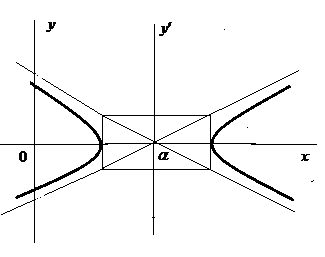
определяет гиперболу, смещенную вдоль оси ОУ и её можно привести к каноническому уравнению вида
или
(2.4)
где
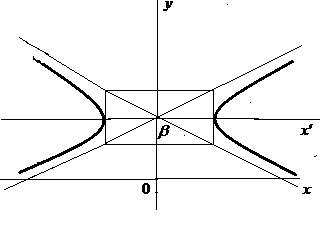
Рассмотрим возможные случаи
(
)
(
)
Выполните самостоятельно.
Задача 7. Составить уравнение гиперболы,
если ее вершины находятся в точках
B(0;4), D(0;-4) и
фокусы в точках (0;
5).
Ответ:
3.5.2 Составление уравнения гиперболы по координатам ее фокусов (расстоянию между фокусами) и ее эксцентриситету.
Задача 10.
Составить уравнение гиперболы, фокусы которой находятся в точках F1(0;-5), F2(0;5), а эксцентриситет
Решение: Найдем фокальное расстояние
F1F2
:
,
т.е. 2с=10, с=5. Так как фокусы по условию
задачи расположены на оси оу, то по
формуле (9)
имеем
.
Подставив в полученное равенство
значение с получим:
,
откуда b=3.
По формуле (?) найдем а2=25-9=16, а=4.
Подставив значения a и b
в уравнение (?) получим
или
Задача 11.Составить уравнение гиперболы по координатам фокусов F( 20;0) и эксцентриситету .
Ответ:
3.5.3 Составления уравнения гиперболы по длине ее действительной оси и эксцентриситету.
Задача 13.
Решение комплексных задач на составление уравнений линий первого и второго порядков
6.1 Найти длину перпендикуляра, опущенного
из начала координат на прямую, проходящую
через центр окружности
и
фокус параболы
Решение
1 Найдем координаты центра окружности
Запишем уравнение окружности в стандартном виде и в левой части выделим полный квадрат:
.
Найдем координаты фокуса параболы
Запишем уравнение параболы в стандартном
виде
.
Сравним уравнение данной параболы с
каноническим уравнением
.
Осью симметрии параболы является ось
ОУ, ветви её направлены вниз, а фокусы
находятся в точке
.
В данном случае
,
тогда
.
Составим уравнение прямой, проходящей через центр окружности и фокус параболы, используя уравнение прямой, проходящей через две точки
Длину перпендикуляра вычислим, по формуле для вычисления расстояния от точки
до
прямой
Ответ:
