
- •Гипербола. Уравнения гиперболы. Исследование уравнения гиперболы
- •4.1 Определение гиперболы
- •4.2 Каноническое уравнение гиперболы
- •4.3 Исследование канонического уравнения гиперболы
- •4.3.1 Симметрия гиперболы
- •4.3.2 Точки пересечения с осями координат
- •4.3.3 Изменение координат точек гиперболы (форма гиперболы)
- •Асимптоты гиперболы
- •4.5 Сопряженные гиперболы
- •4.6 Равносторонняя гипербола
- •4.7 Основные элементы гиперболы
- •4.7.1 Эксцентриситет гиперболы
- •4.7.2 Фокальные радиусы
- •4.7.3 Директрисы гиперболы
- •4.7.4 Касательная к гиперболе
- •Диаметры гиперболы
- •4.8 Решение задач на определение основных элементов гиперболы
- •4.9 Составление канонического уравнения гиперболы по условиям, которые её определяют
- •4.8.1 Составление уравнения гиперболы по координатам его вершин (длине действительной оси) и координатам фокусов ( фокальному расстоянию)
- •1Т.К.Фокусы гиперболы ,то действительная ось и уравнение гиперболы имеет
- •4.8.2 Составление уравнения гиперболы по координатам его вершин ( длине действительной оси) и эксцентриситету
- •4.8.3 Составление уравнения гиперболы по координатам ее фокусов (расстоянию между фокусами) и эксцентриситету
- •4.8 Уравнение гиперболы со смещенным центром (смещенная гипербола)
- •4.8.1 Связь общего уравнения кривых второго порядка с общим уравнением гиперболы
- •4.8.2 Расположение гиперболы в декартовой системе координат в зависимости от коэффициентов d и e
4.3.3 Изменение координат точек гиперболы (форма гиперболы)
Для того, чтобы установить пределы изменения координат точек гиперболы разрешим уравнение (4.1) относительно x и y, получим:
![]()
Так
как гипербола симметричная кривая (см.
«Симметрия гиперболы»), то исследование
можно провести и построить гиперболу
только в I четверти,
т.е. на интервале
![]() ,а
затем симметрично отобразить.
,а
затем симметрично отобразить.
Найдем область определения функции:
![]()
![]() ,
откуда
,
откуда
![]() или
или
![]()
Раскроем знак модуля, получим:
![]()
Вывод. Абсциссы точек гиперболы
меняются от
![]() до –а и от а до
до –а и от а до![]() .
.
Найдем область определения функции:
![]()
![]() - любое
- любое
Вывод. Гипербола располагается в
полуплоскостях правее прямой
![]() и левее
и левее
![]() (рис.23)
(рис.23)
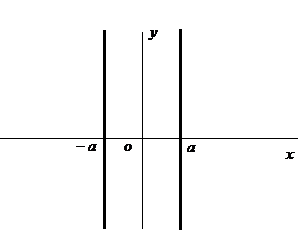
Рис.23
Асимптоты гиперболы
 Прямая
Прямая
![]() ,
к которой приближается как угодно близко
точка кривой (ветви кривой) при движении
ее вдоль кривой к бесконечности,
называется асимптотой гиперболы.
,
к которой приближается как угодно близко
точка кривой (ветви кривой) при движении
ее вдоль кривой к бесконечности,
называется асимптотой гиперболы.
Обратимся к диагоналям прямоугольника MNKL, составим уравнение прямой OK (рис.22):
![]()
Для составления уравнения прямой
воспользуемся уравнением «пучка»
![]() ,
тогда
,
тогда
![]() .
.
Запишем уравнение прямой в общем виде:
![]()
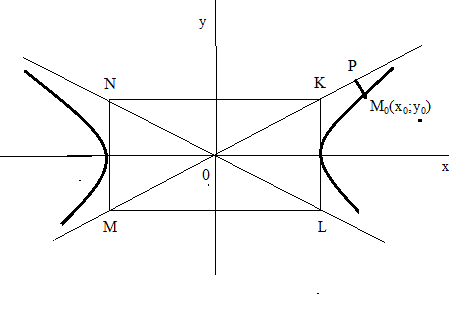
Рис.24
Найдем расстояние от точки гиперболы
![]() до прямой OK, используя
формулу вычисления расстояния от точки
до прямой.
до прямой OK, используя
формулу вычисления расстояния от точки
до прямой.
![]()
Помножим числитель и знаменатель дроби
на
![]() ,
получим
,
получим
![]()
Так как M0(x0,
y0) – точки гиперболы,
то ее координаты удовлетворяют уравнению
гиперболы (1), тогда
![]() (См.
«Вывод уравнения гиперболы»),
тогда:
(См.
«Вывод уравнения гиперболы»),
тогда:
![]()
Из полученной формулы следует, что если
![]() двигается по гиперболе так, что ее
абсцисса x0
неограниченно возрастает (значит
возрастает знаменатель дроби), то ее
расстояние до прямой
двигается по гиперболе так, что ее
абсцисса x0
неограниченно возрастает (значит
возрастает знаменатель дроби), то ее
расстояние до прямой
![]() неограниченно убывает, то есть
- асимптота гиперболы.
неограниченно убывает, то есть
- асимптота гиперболы.
То же обстоятельство будет иметь место при движении точки M по гиперболе в третьей четверти (вследствие симметрии относительно начала координат).
Наконец, вследствие симметрии гиперболы
относительно оси OY мы
получим вторую прямую
![]() ,
симметрично расположенную с прямой
,
к которой также будет неограниченно
приближаться точка M при
движении по гиперболе и удалении в
бесконечность (во второй и четвертой
четвертях).
,
симметрично расположенную с прямой
,
к которой также будет неограниченно
приближаться точка M при
движении по гиперболе и удалении в
бесконечность (во второй и четвертой
четвертях).
Эти две прямые носят название асимптоты гиперболы (рис 25).
Уравнения асимптот гиперболы:
![]() (4.4)
(4.4)
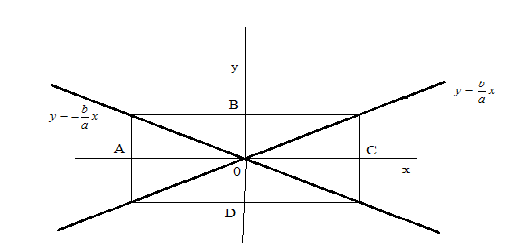
Рис.25
Асимптоты гиперболы располагаются по диагоналям «основного» прямоугольника гиперболы, одна сторона которого параллельна оси OX и равна 2a, другая – параллельна оси OY и равна 2b, а центр лежит в начале координат.
При построении гиперболы по ее уравнению нужно предварительно построить ее асимптоты.
Выполним построение гиперболы (рис.26)
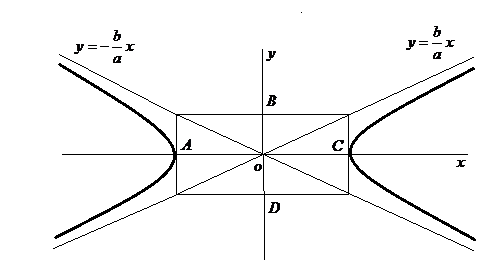
Рис.26
Аналогично можно провести исследование уравнения (4.2)
и построить гиперболу (рис.27)
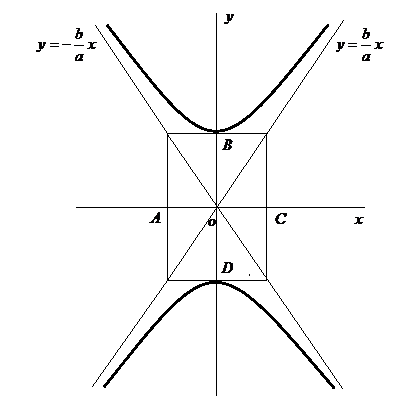
Рис.27
