7.5 Задача о распределении ресурсов

Малое предприятие выпускает два вида деталей. На их изготовление идет три вида ресурсов R₁, R₂, R₃, выделяемых предприятию в ограниченных количествах.

Данные о наличии и расходе материалов, себестоимость 1000 шт. деталей каждого вида, а также оптовая цена за 1000 шт. приведены в табл. 7.5.1.

Таблица 7.5.1

Виды материалов	Запасы (усл. ед.)	Расход материалов на 1000 ед деталей (усл. ед)
		Деталь А	Деталь В
R1	216	12	18
R2	224	14	16
R3	200	20	10
Себестоимость 1000 шт. (усл. ед.)		3,8	3,5
Оптовая цена 1000 шт. (усл. ед.)		5	6

Необходимо составить план выпуска деталей, обеспечивающий получение максимальной прибыли.

Построение математической модели

Обозначим: Х₁ - число выпускаемых деталей А (в тысячах штук);

Х₂ - число выпускаемых деталей В (в тысячах штук).

1. Определение ограничений

На неизвестные величины накладываются два вида ограничений:

Первое. По физическому смыслу (число деталей неотрицательно)

Х ₁ ≥ 0;

Х₂ ≥ 0.

Второе. По запасам ресурсов:

1 2Х₁ + 18Х₂ ≤ 216

14Х₁ + 16Х₂ ≤ 224

20Х₁ + 10Х₂ ≤ 200

2. Определение целевой функции

Для расчета целевой функции (прибыли от продажи выпускаемых деталей) рассчитаем прибыль, получаемую от тысячи деталей каждого вида.

Для деталей А: 5-3,8=1,2.

Для деталей В: 6-3,5=2,5.

Тогда целевая функция равна

Z=1,2X₁+2,5X₂

Требуется найти такие значения неизвестных X₁ и Х₂, которые обеспечивают максимум целевой функции при выполнении ограничений.

Построение начального плана решения

План решения аналогичен описанному в предыдущей задаче.

Создайте в книге MS Excel лист, в который внесите исходные данные как показано в таблице 7.5.2.

Сначала будем считать, что план выпуска составляет одну деталь А и одну деталь В (ячейки А12:В12)

Прибыль, получаемую от тысячи деталей каждого вида, рассчитаем в ячейках С12:D12. Целевую функцию занесем в ячейку Е12.

Перенесем данные о расходе материалов на 1000 деталей из исходной таблицы в ячейки А15:В17.

В ячейках D15:Е17 разместим данные для проверки выполнения системы ограничений.

Оптимизация плана решения

Алгоритм оптимизации аналогичен описанному в задаче планирования выпуска продукции. Диалоговое окно Поиска решения приведено на рис. 7.5.1 - а оптимальный план решения - в табл. 7.5.3.

Таблица 7.5.2

	А	В	С		D		E
1	Виды материалов	Запасы (усл. ед.)	Расход материалов на 1000 ед деталей (усл. ед)
2			Деталь А		Деталь В
3	R1	216	12		18
4	R2	224	14		16
5	R3	200	20		10
6	Себестоимость 1000 шт. (усл. ед.)			3,8		3,5
7	Оптовая цена 1000 шт. (усл. ед.)			5		6
8
9	Задача распределения ресурсов
10	План выпуска			Целевая функция
11	Деталь А	Деталь В	Прибыль от 1000 деталей А		Прибыль от 1000 деталей В		Значение целевой функции
12	1	1	1,2		2,5		3,7
13	Ограничения
14	Расход материала на 1000 деталей					Левая часть системы		Правая часть системы
15	12	18	для R1		30		216
16	14	16	для R2		30		224
17	20	10	для R3		30		200

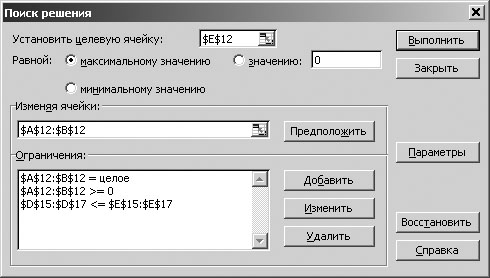
Рисунок 7.5.1

Таблица 7.5.3

	А	В		С		D			E
9	Задача распределения ресурсов
10	План выпуска			Целевая функция
11	Деталь А	Деталь В		Прибыль от 1000 деталей А		Прибыль от 1000 деталей В			Значение целевой функции
12	0	12		1,2		2,5			30
13	Ограничения
14	Расход материала на 1000 деталей						Левая часть системы		Правая часть системы
15	12		18		для R1			216		216
16	14		16		для R2			192		224
17	20		10		для R3			120		200

КОНТРОЛЬНОЕ ЗАДАНИЕ

Предприятие выпускает три вида продукции. На их изготовление идет три вида сырья R₁, R₂, R₃, имеющихся в ограниченном количестве.

Необходимо составить план выпуска деталей, обеспечивающий получение максимальной прибыли, при условии, что норма прибыли одинакова для всех видов продукции и составляет 20%.

Данные о наличии и расходе и стоимости сырья приведены в таблице:

Виды сырья	Стоимость сырья, тыс.руб./кг	Запасы (усл. ед.)	Расход сырья на ед. продукции, кг.
			Деталь А	Деталь В	Деталь С
R1	0,4+n/10	200+n	2	2	3
R2	0,2+n/10	250+n	2	3	4
R3	0,3+n/10	140+n	1	2	1

Коэффициент n равен номеру варианта.

ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ

1. Назовите надстройку Excel, используемую для оптимизации решений.

2. Дайте определение понятию Целевая функция задачи.

3. Можно ли использовать математическую модель одной задачи для оптимизации другой задачи?

4. Можно ли провести оптимизацию решения без ввода ограничений?

5. Может ли задача, решаемая в Excel, иметь несколько целевых функций?

Рекомендованная литература:

1. Алесинская Т.В. Учебно-методическое пособие по курсу "Экономико-математические методы и модели. Линейное программирование"/ Т.В.Алесинская, В.Д.Сербин, А.В.Катаев — Таганрог: Изд-во ТРТУ, 2001. — 79 с.

2. Боброва Л.В., Информатика в управлении и экономике: учеб. пособие / Л.В. Боброва, О.И.Золотов, Е.А. Рыбакова — СПб.: Изд-во СЗТУ, 2005. — 258с.

3. Десятирикова Е.Н. Анализ количественных методов оценки рисков / Десятирикова Е.Н., Слинькова Н.В. // Информатика: проблемы, методология, технологии: сборник докладов IX Международной конференции 12-13 февраля 2009г. – Воронеж -2009

4. Десятирикова Е.Н. Инвестиционное проектирование и управление рисками / Десятирикова Е.Н., Слинькова, Н.В. // Кибернетика и высокие технологии XXI века: материалы VI международной научно-технической конференции 17-19 мая 2005г. - Воронеж -2005 - с.95-99

5. Десятирикова Е.Н. Информационные технологии управления: учеб. пособие для высших учебных заведений. — Воронеж, 1998 — 172с.

6. Десятирикова Е.Н. Оценка и анализ рисков инвестиционных проектов / Десятирикова Е.Н., Слинькова, Н.В. // Экономическое прогнозирование: модели и методы: материалы Международной научно-практической конференции 29 – 30 апреля 2005г.: в 2ч. // под ред. проф. В.В.Давниса. – Воронеж: Воронежский Государственный университет – 2005 – Ч.2.

7. Инвестиции: учебное пособие / Г.П. Подшиваленко, Н.И. Лахметкина, М.В. Макарова [и др.]. — 3-е изд., перераб. и доп. — М.: КНОРУС, 2006. — 200 с.

8. Информационные системы в экономике: учебник / под ред. Г.А. Титоренко — 2 изд., перераб. и доп. — М.: Юнити-Дана, 2008 — 463с.

9. Ковалев В.В. Анализ хозяйственной деятельности предприятия: учебник для ВУЗов / В.В. Ковалев, О.Н. Волкова — Проспект, 2008. — 421с.

10. Орел А. А. Информационные системы: учебное пособие / А. А. Орел, О.М. Ромакина. — Саратов, 2004 — 87 с.

11. Орлов А.И. Теория принятия решений : Учебное пособие. - М.: Издательство "Март", 2004. — 656с.

12. Ракитина Е.А. Информатика и информационные системы в экономике: Учеб. пособие. Ч. 1. / Е.А. Ракитина, В.Л. Пархоменко — Тамбов: Изд-во тамб. гос. техн. ун-та, 2005.— 148 с.

13. Трифонов Ю.В. Выбор эффективных решений в экономике в условиях неопределённости / Трифонов Ю.В., Плеханова А.Ф., Юрлов Ф.Ф. - Н. Новгород: Издательство ННГУ, 1998г.

14. Четыркин Е.М. Финансовый анализ производственных инвестиций - М.: Дело, 1998.