7.4 Задача планирования выпуска продукции

Предприятие выпускает два вида деталей. Оно закупает заготовки, подвергаемые обработке на станках трех типов: S1, S2, S3. Данные, характеризующие производительность станочного парка, а также стоимостные характеристики, приведены в табл. 7.4.1.

Таблица 7.4.1

	А	В	С	D
1	Станки		Производительность станков (шт/час)
2	Вид	Стоимость часа работы (у.е)	Деталь А	Деталь В
3	S1	24	30	30
4	S2	21	50	25
5	S3	18	20	40
6	Стоимость одной заготовки (у.е)		30	40
7	Продажная цена одной детали (у.е)		59,5	79,89

Предполагая, что можно выпустить любую комбинацию деталей А и В, найти план выпуска продукции, максимизирующий прибыль.

Построение математической модели

Создайте в книге MS Excel лист с названием «Дано», в который внесите исходные данные как показано в таблице 7.4.1.

1. Расчет прибыли на одну деталь

Рассчитаем прибыль на одну деталь. Расчеты сведем в табл. 7.4.2 (режим показа формул приведен в таблице 7.4.3).

Таблица 7.4.2

	А	В		С		D
1	Затраты на обработку одной детали (у.е.)			Деталь А		Деталь В
2	Стоимость обработки детали на одном станке (у.е.)		S1		0,8		0,8
3			S2		0,42		0,84
4			S3		0,9		0,45
5	Общие затраты на обработку (у.е.)			2,12		2,09
6	Покупная цена заготовки (у.е.)			30		40
7	Общие затраты на одну деталь (у.е.)			32,12		42,09
8	Продажная цена одной детали (у.е)			59,5		79,89
9	Прибыль на одну деталь (у.е.)			27,38		37,8

Таблица 7.4.3

	А	В	С	D
1	Затраты на обработку одной детали (у.е.)		Деталь А	Деталь В
2	Стоимость обработки детали на одном станке (у.е.)	S1	=Дано!B3/Дано!C3	=Дано!B3/Дано!D3
3		S2	=Дано!B4/Дано!C4	=Дано!B4/Дано!D4
4		S3	=Дано!B5/Дано!C5	=Дано!B5/Дано!D5
5	Общие затраты на обработку (у.е.)		=СУММ(C2:C4)	=СУММ(D2:D4)
6	Покупная цена заготовки (у.е.)		=Дано!C6	=Дано!D6
7	Общие затраты на одну деталь (у.е.)		=СУММ(C5:C6)	=СУММ(D5:D6)
8	Продажная цена одной детали (у.е)		=Дано!C7	=Дано!D7
9	Прибыль на одну деталь (у.е.)		=C8-C7	=D8-D7

2. Расчет целевой функции

Рассчитаем целевую функцию - прибыль предприятия от деталей, изготовляемых за один час работы.

Обозначим: Х₁- число выпускаемых в час деталей А;

Х₂ - число выпускаемых в час деталей В.

Тогда чистая прибыль за час составит

Z = 27,38×X₁+37,8×X₂

3. Определение ограничений

Значения Х нельзя выбирать произвольно. Рассмотрим ограничения, накладываемые на эти переменные. Таких ограничений два.

Первое. По физическому смыслу переменных. Количество выпускаемых деталей не может быть отрицательным, т.е.

Х₁ ≥ 0;

Х₂ ≥ 0.

Второе. По мощности оборудования.

Для станка S1. На этом станке в час может быть обработано 30 деталей А или 30 деталей В, отсюда получаем неравенство

X₁/30 + Х₂/30 ≤ 1

Для станка S2. На этом станке в час может быть обработано 50 деталей А или 25 деталей В, отсюда получаем неравенство

Х₁/50 + Х₂/25 ≤ 1

Для станка S3. На этом станке в час может быть обработано 20 деталей А или 40 деталей В, отсюда получаем неравенство

Х₁/20 + Х₂/40 ≤ 1

Сведем уравнения второго ограничения в систему:

X ₁/30 + Х₂/30 ≤ 1

Х₁/50 + Х₂/25 ≤ 1

Х₁/20 + Х₂/40 ≤ 1

Избавляясь от знаменателей в системе уравнений (12.15), получаем

X ₁ + Х₂ ≤ 30

Х₁ + 2Х₂ ≤ 50

2Х₁ + Х₂ ≤ 40

Итак, математическую модель задачи составляют уравнение и неравенства. Нужно найти такие значения переменных X₁ и Х₂, которые доставляют максимум целевой функции при выполнении ограничений.

Разработка начального плана выпуска продукции

1) В ячейках В3:С4 (табл. 7.4.4) разместим исходные данные о переменных Х₁ и Х₂. Будем считать, что план выпуска составляет одну деталь А в час и одну деталь В в час.

2) В ячейках Е3:F5 поместим данные о коэффициентах левой части системы неравенств.

3) В строках 7-8 введем информацию о целевой функции:

а) в ячейках В8 и С8 разместим коэффициенты (значения прибыли на одну деталь) перед переменными в целевой функции Z из уравнения, описывающего расчет прибыли;

б) в ячейку E8 введем формулу для вычисления значения ЦФ. Можно ввести формулу =В4*В8+С4*С8, а можно воспользоваться функцией =СУММПРОИЗВ(В4:С4;В8:С8).

4) В строках 10-13 разместим данные для проверки выполнения системы ограничений.

а) в ячейку B11 введем формулу для вычисления левой части первого неравенства из системы. Это может быть формула =B4*E3+C4*F3. Но лучше воспользоваться общей формулой — функцией

=СУММПРОИЗВ(В4:С4;Е3:F3).

б) чтобы скопировать эту формулу в другие ячейки, следует запретить изменять адреса ячеек В4:С4 при копировании. Введем знаки доллара, получим формулу =СУММПРОИЗВ(В$4:С$4;Е3:F3).

в) Копируем формулу в ячейки B12:B13. В ячейке B12 формула =СУММПРОИЗВ(В$4:С$4;Е4:F4). В ячейке B13 формула =СУММПРОИЗВ(В$4:С$4;Е5:F5).

5) В ячейки E11:E13 введем правые части неравенства системы.

Таблица 7.4.4

	А		В		С		D		E		F
1	Оптимизация плана выпуска продукции
2	Переменные (число выпускаемых в час деталей)						Коэффициенты при неизвестных в системе ограничений
3	ИМЯ	X1		Х2		для S1		1		1
4	ЗНАЧЕНИЕ	1		1		для S2		1		2
5						для S3		2		1
6	Целевая функция
7	Коэффициенты при переменных (значения прибыли на одну деталь)						Значение целевой функции (Чистая прибыль)
8		27,38		37,80				65,18
9	Система ограничений
10	Значения левой части						Правая часть
11		2						30
12		3						50
13		3						40

Оптимизация плана выпуска

1) Запускаем режим «Поиск решения». Для этого выполним команды Сервис  Поиск решения. Появится окно Поиска решения (рис. 7.4.1).

2) В поле Установить целевую ячейку ввести $E$8

3) Выбрать режим поиска:  Максимальное значение.

4) В поле Изменяя ячейки ввести В4:С4

5) Чтобы ввести ограничения, щелкнуть по кнопке Добавить. Появится окно Изменение ограничений.

6) Ввести ограничения:

В4:С4≥0;

В4:С4 = целое;

B11:B13≤E11:E13.

После каждого ограничения щелкнуть по кнопке Добавить, после последнего Ок.

7) Щелкнуть по кнопке Выполнить. В результате получим оптимальный план выпуска продукции (табл. 7.4.5).

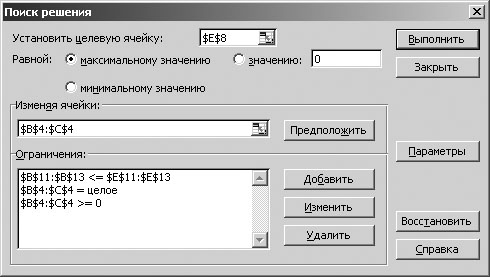
Рисунок 7.4.1

Таблица 7.4.5

	А		В	С		D		E		F
1	Оптимизация плана выпуска продукции
2	Переменные (число выпускаемых в час деталей)						Коэффициенты при неизвестных в системе ограничений
3	ИМЯ	X1			Х2		для S1		1		1
4	ЗНАЧЕНИЕ	10,0			20,0		для S2		1		2
5							для S3		2		1
6	Целевая функция
7	Коэффициенты при переменных (значения прибыли на одну деталь)						Значение целевой функции (Чистая прибыль)
8		27,38			37,80				1029,8
9	Система ограничений
10	Значения левой части						Правая часть
11		2							30
12		3							40
13		3							50

КОНТРОЛЬНОЕ ЗАДАНИЕ

Предприятие выпускает два вида деталей. Оно закупает заготовки, подвергаемые обработке на станках двух типов: S1, S2. Предполагая, что можно выпустить любую комбинацию деталей А и В, найти план выпуска продукции, максимизирующий прибыль.

Данные, характеризующие производительность станочного парка, а также стоимостные характеристики, приведены в таблице:

Станки		Производительность станков (шт/час)
Вид	Стоимость часа работы (у.е)	Деталь А	Деталь В
S1	24+n	30	30
S2	18+n	20	40
Стоимость одной заготовки (у.е)		30+2n	40+2n
Продажная цена одной детали (у.е)		59,5+3n	79,89+3n

Коэффициент n равен номеру варианта.