
- •Десятирикова е.Н., Слинькова н.В. Информационные технологии управления Учебное пособие
- •Часть 1
- •Сведения об авторах
- •Оглавление
- •1. Информационные технологии в управлении
- •1.1 Сущность и виды информационных технологий
- •Автоматизированные рабочие места
- •1.2. Основы применения табличных процессоров для решения управленческих задач
- •1. Вычитание дат.
- •2. Сложение дат с числами.
- •2. Финансовый анализ
- •2.1 Основы финансовых вычислений
- •2.2 Финансовые вычисления в Excel
- •3. Оценка инвестиционных проектов
- •3.1 Сущность и оценка инвестиционных проектов
- •3.2 Основные показатели, используемые для оценки инвестиционных проектов
- •3.3 Сравнение инвестиционных проектов с помощью Excel
- •3.4 Учет влияния процентной ставки на эффективность проекта с использованием Excel
- •3.5 Оценка эффективности инвестиционных проектов с учетом риска
- •Задание 1 (учет риска в знаменателе формулы npv посредством корректировки ставки дисконта)
- •Решение:
- •Задание 1.2 (учет риска в числителе формулы npv посредством корректировки чистых денежных потоков)
- •Решение:
- •3.6 Оценка эффективности инвестиционного проекта с помощью построения «дерева решений»
- •Задание 1
- •Решение:
- •3.7 Анализ чувствительности инвестиционного проекта
- •Задание 1
- •Решение:
- •1) Чувствительность проекта к изменению цены реализации
- •2) Чувствительность проекта к изменению объема реализации
- •3) Чувствительность проекта к изменению постоянных затрат
- •4) Чувствительность проекта к изменению переменных затрат
- •4. Задачи анализа и прогнозирования
- •4.1 Прогнозирование как основа выработки управленческой стратегии
- •4.2 Балансовая модель
- •4.3 Прогнозирование с использованием регрессионного анализа
- •5. Системы принятия решения
- •5.1 Краткие сведения о системах принятия решения (экспертных системах)
- •Классификация задач принятия решений
- •Экспертные системы ( эс)
- •Структура экспертной системы
- •5.2 Разработка системы принятия решения
- •Самостоятельное задание Разработка системы принятия решений о продаже акций предприятия
- •6. Выбор оптимальных коммерческих стратегий
- •Принятие решений в условиях риска
- •1. Максиминный критерий Вальда
- •2. Минимаксный критерий Сэвиджа
- •3. Критерий Гурвица
- •Задание 1
- •Решение:
- •1) Выбор оптимальной стратегии по критерию Вальда.
- •2) Выбор оптимальной стратегии по критерию Сэвиджа.
- •3) Выбор оптимальной стратегии по критерию Гурвица.
- •7. Оптимизация управленческих задач
- •7.1 Принципы решения задач оптимизации
- •7.2 Транспортная задача
- •Стандартная транспортная модель
- •Сбалансированная транспортная модель
- •Многопродуктовая транспортная модель
- •Решение транспортной задачи в Excel
- •Разработка начального плана решения
- •Улучшение (оптимизация) плана перевозок
- •7.3 Определение графика работы сотрудников фирмы
- •1. Построение математической модели
- •2. Оптимизация решения
- •7.4 Задача планирования выпуска продукции
- •7.5 Задача о распределении ресурсов
4.2 Балансовая модель
Одна из серьезнейших задач, стоящих перед любым управляющим и экономистом - на основе анализа деятельности предприятия за прошлый период осуществить планирование его деятельности в следующем периоде. Рассмотрим задачу планирования производства на примере балансовой модели.
Задание 1
Экономическая система состоит их трех отраслей. Объемы производства каждой из отраслей за предыдущий период, текущее производственное потребление в отраслях, а также прогнозируемый конечный спрос продукции каждой из трех отраслей приведены в таблице 4.2.1. Определить конечную продукцию каждой из отраслей за предыдущий период и план выпуска продукции в следующем периоде, считая, что технология производства не изменилась.
Таблица 4.2.1
Отрасли
|
Объемы производства отраслей
|
Производственное потребление отраслей за предыдущий период |
Прогнозируе-мый конечный спрос |
|||
1 |
2 |
3 |
||||
1 2 3 |
600 1000 800 |
250 150 0 |
100 500 300 |
160 0 400 |
2000 2000 3000 |
|
Математическая постановка задачи
Для решения поставленной задачи можно использовать балансовую модель Леонтьева. Она представляет собой систему уравнений, каждое из которых выражает требование равенства (баланса) между количеством продукции, производимой отдельным экономическим объектом, и совокупной потребностью в этой продукции. В рассматриваемой задаче экономическая система состоит из трех отраслей.
Пусть Хi — величина, равная суммарному выпуску продукции отрасли i;
Хij - количество продукции отрасли i, необходимое для того, чтобы отрасль j произвела Хj единиц своей продукции;
Yj - количество продукции отрасли i, оставшейся для внешнего потребления (конечная продукция).
Тогда взаимосвязь отраслей в процессе производства и потребления отдельного продукта Xi (i= 1, 2, 3) может быть описана в виде следующих уравнений:
Х1 = х11+х12+х13+Y1;
Х2 = х21+х22+х23+Y2;
Х3 = х31+х32+х33+Y3.
Используем понятие коэффициентов прямых затрат (технологических коэффициентов) аij:
 - количество
продукции отрасли i,
необходимое для того, чтобы отрасль j
произвела одну единицу своей продукции.
- количество
продукции отрасли i,
необходимое для того, чтобы отрасль j
произвела одну единицу своей продукции.
Тогда xij=aijXj и система уравнений будет иметь следующий вид:
Х1 = a11X1+a12X2+a13X3+Y1;
Х2 = a21X1+a22X2+a23X3+Y2;
Х3 = a31X1+a32X2+a33X3+Y3.
Или в матричной форме
X=AX+Y,
где A
=
 -
матрица прямых затрат;
-
матрица прямых затрат;
Х-
вектор-столбец выпуска продукции в
предыдущем периоде X =
 ;
;
Y
- вектор-столбец конечного спроса в
предыдущем периоде Yc
=

Решим уравнение X=AX+Y относительно X:
X-AX=Y,
отсюда,
Х(Е-А)=Y,
где Е - единичная матрица. Из уравнения получаем X=(Е-А)-1Y
Решение задачи
Определение вектора конечной продукции за предыдущий период
По условию задачи известны объемы производства каждой из отраслей за предыдущий период (суммарный выпуск продукции отрасли i): X1=600, Х2=1000, Х3= 800 и значения xij (i,j = 1, 2, 3):
х11=250; х12=100; х13=160
х21=150; х22=500; х23=0;
х31=0; х32=300; х33=400.
Отсюда, используя, можно определить значения Yi, i=1,2,3 конечной продукции каждой из отраслей за предыдущий период.
Y1 =600-250-100-160=90;
Y2 =1000-150-500-0=350;
Y3 =800-0-300-400=100.
Таким образом, вектор конечной продукции за предыдущий период найден:
Yn
=

Для определения
вектора выпуска продукции X
при заданном конечном прогнозируемом
векторе спроса Y
=
 надо решить систему уравнений, из которой
следует, что
надо решить систему уравнений, из которой
следует, что
X=(Е-А)-1Y
где Е - единичная матрица
Е
=
S=(E-A)-1 - называется матрицей полных затрат.
Определение коэффициентов прямых затрат
Учитывая, что технология производства не изменилась, определим коэффициенты прямых затрат aij.
a11=250/600=0,417; a12=100/1000=0,1; a13=160/800=0,2
a21=150/600=0,25; a22=500/1000=0,5; a23=0/800=0;
a31=0/600=0; a32=300/1000=0,3; a33=400/800=0,5.
Таким образом, матрица коэффициентов прямых затрат будет иметь вид
А
=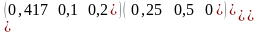
Проверка продуктивности матрицы
Все элементы матрицы А неотрицательные, А≥0.
Для того чтобы система уравнений имела единственное неотрицательное решение при любом неотрицательном векторе Y, необходимо, чтобы матрица А была продуктивной. Экономический смысл продуктивности состоит в том, что существует такой план выпуска продукции, при котором каждая отрасль сможет произвести некоторое количество конечной продукции. Известно, что для продуктивности матрицы А≥0 необходимо и достаточно, чтобы все главные миноры матрицы (Е-А) были положительными числами, строго меньше единицы. Кроме того, если сумма элементов каждого из столбцов неотрицательной квадратной матрицы положительна и строго меньше единицы, то все главные миноры матрицы (Е-А) положительны и строго меньше единицы.
Суммы элементов каждого столбца матрицы А соответственно равны:
0,417 + 0,25 + 0 = 0,667;
0,1 + 0,5 + 0,3 = 0,9;
0,2 + 0 + 0,5 = 0,7.
Следовательно, в силу вышесказанного, матрица А продуктивна, выражение X=(Е-А)-1Y имеет смысл и вектор Y неотрицателен. Следовательно, для нахождения плана выпуска продукции Xможно воспользоваться формулой X=(Е-А)-1Y.
Вычисление матрицы Е-А
Вычислим матрицу (Е-А):
E-A
=
-
=
Вычисление обратной матрицы (Е-А)-1
Известно, что матрица В-1 называется обратной по отношению к квадратной матрице В, если произведение В×В-1=Е (Е - единичная матрица).
Для вычисления обратной матрицы воспользуемся формулой:
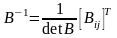
Здесь [Bij] - матрица, полученная из элементов Bij, a Bij - алгебраические дополнения элементов ij матрицы.
Вij=(-1) i+jMij
где Мij - минор элемента Bij (минор - это такой определитель, который получается из матрицы вычеркиванием строки и столбца, на пересечении которых стоит данный элемент).
Вычислим значения алгебраических дополнений элементов матрицы (Е-А). Обозначим для простоты описания вычислений Е-А=В:
B11
= (-1)1+1 = 0,25
= 0,25
B12
= (-1)1+2 = 0,125
= 0,125
B13
= (-1)1+3 = 0,075
= 0,075
B21
= (-1)2+1 = 0,11
= 0,11
B22
= (-1)2+2 = 0,292
= 0,292
B23
= (-1)2+3 = 0,075
= 0,075
B31 = (-1)3+1 = 0,1
B32 = (-1)3+2 = 0,05
B33 = (-1)3+3 = 0,267
Таким образом,
[E-A]
= [Bij]
=

Вычисление транспонированной матрицы
Поменяв в матрице [Е-А] строки и столбцы местами, получаем:
[E-A]T
= [Bij]
T=

Вычисление определителя матрицы [Е-А]
Вычислим определитель, применив разложение по первой строке
det(Е-А)= 0,583× - (-0,1)× - (-0,2)× = 0,018
Вычисление матрицы прямых затрат S
По формуле S=(E-A)-1
=
= =
=
=

Определение вектора выпуска продукции X
Зная S и Y, вычислим Х по формуле:
Х = S×Y
=
×

Отсюда
Х1 = 2,113 × 2000 + 0,93 × 2000 + 0,845 × 3000 = 8620;
Х2 = 1,056 × 2000 + 2,465 × 2000 + 0,423 × 3000 = 8310;
Х3 = 0,634 × 2000 + 1,479 × 2000 + 2,254 × 3000 = 10986.
Таким образом, вектор выпуска продукции в следующем периоде при заданном векторе конечной продукции
Yc
=
Х
=
Очевидно, что с использованием матричных операций в Excel процедура вычислений в балансовой модели существенно упростится.
Реализация балансовой модели в электронной таблице Excel показана в табл. 4.2.2 (режим показа формул) и в табл. 4.2.3 (режим вычислений).
Таблица 4.2.2
|
A |
B |
C |
D |
|
1 |
БАЛАНСОВАЯ МОДЕЛЬ |
||||
2 |
Объём производства |
Потребление отраслей |
|||
3 |
600 |
250 |
100 |
160 |
|
4 |
1000 |
150 |
500 |
0 |
|
5 |
800 |
0 |
300 |
400 |
|
6 |
Вычисление технологических коэффициентов |
=B3/A$3 |
=C3/A$4 |
=D3/A$5 |
|
7 |
=B4/A$3 |
=C4/A$4 |
=D4/A$5 |
||
8 |
=B5/A$3 |
=C5/A$4 |
=D5/A$5 |
||
9 |
Проверка продуктивности матрицы А |
||||
10 |
|
=СУММ(B6:B8) |
=СУММ(C6:C8) |
=СУММ(D6:D8) |
|
11 |
=ИЛИ(B10>=1;C10>=1;D10>=1) |
=ЕСЛИ(A11="ИСТИНА";"Решения нет"; "Матрица продуктивна") |
|||
12 |
Единичная матрица |
1 |
0 |
0 |
|
13 |
0 |
1 |
0 |
||
14 |
0 |
0 |
1 |
||
15 |
Вычисление Е-А |
=B12-B6 |
=C12-C6 |
=D12-D6 |
|
16 |
=B13-B7 |
=C13-C7 |
=D13-D7 |
||
17 |
=B14-B8 |
=C14-C8 |
=D14-D8 |
||
18 |
Вычисление обратной матрицы |
=МОБР(B15:D17) |
=МОБР(B15:D17) |
=МОБР(B15:D17) |
|
19 |
=МОБР(B15:D17) |
=МОБР(B15:D17) |
=МОБР(B15:D17) |
||
20 |
=МОБР(B15:D17) |
=МОБР(B15:D17) |
=МОБР(B15:D17) |
||
21 |
Спрос на будущий период |
2000 |
План выпуска продукции |
=МУМНОЖ(B18:D20;B21:B23) |
|
22 |
2000 |
=МУМНОЖ(B18:D20;B21:B23) |
|||
23 |
3000 |
=МУМНОЖ(B18:D20;B21:B23) |
|||
В строке 11 размещены формулы для проверки продуктивности матрицы технологических коэффициентов.
В ячейке А11 формула
=ИЛИ(B10>=l;C10>=l;D10>=l)
проверяет содержимое ячеек B10:D10. Если хотя бы в одной из этих ячеек значение больше единицы (т.е. сумма значений элементов хотя бы в одном столбце превышает единицу), то в ячейку А11 будет записано значение «ИСТИНА». В противном случае - значение «ЛОЖЬ»;
В ячейку С11 введена формула
=ЕСЛИ(А11="ИСТИНА";"Нет решения";"Матрица продуктивна")
Эта формула проверяет содержимое ячейки А11 и если сумма элементов хотя бы одного столбца превысила единицу, выводит сообщение "Нет решения", в противном случае - "Матрица продуктивна".
Таблица 4.2.3
|
А |
В |
С |
D |
1 |
БАЛАНСОВАЯ МОДЕЛЬ |
|||
2 |
Объём производства |
Потребление отраслей |
||
3 |
600 |
250 |
100 |
160 |
4 |
1000 |
150 |
500 |
0 |
5 |
800 |
0 |
300 |
400 |
6 |
Вычисление технологических коэффициентов |
0,417 |
0,1 |
0,2 |
7 |
0,25 |
0,5 |
0 |
|
8 |
0 |
0,3 |
0,5 |
|
9 |
Проверка продуктивности матрицы А |
|||
10 |
|
0,667 |
0,900 |
0,700 |
11 |
ЛОЖЬ |
Матрица продуктивна |
||
12 |
Единичная матрица |
1 |
0 |
0 |
13 |
0 |
1 |
0 |
|
14 |
0 |
0 |
1 |
|
15 |
Вычисление Е-А |
0,583 |
-0,1 |
-0,2 |
16 |
-0,25 |
0,5 |
0 |
|
17 |
0 |
-0,3 |
0,5 |
|
18 |
Вычисление обратной матрицы |
2,113 |
0,930 |
0,845 |
19 |
1,056 |
2,465 |
0,423 |
|
20 |
0,634 |
1,479 |
2,254 |
|
21 |
Спрос на будущий период |
2000 |
План выпуска продукции |
8619,72 |
22 |
2000 |
8309,86 |
||
23 |
3000 |
10985,92 |
||
