2.3.2 Анализ устойчивости сау с использованием частотного критерия

Устойчивость системы определим с помощью диаграммы Найквиста. Модель замкнутой системы создадим на основе структурной схемы скорректированной системы. Для анализа САУ необходимо использовать передаточную функцию системы в разомкнутом состоянии.

Для начала создаем LTI-объект с именем w, в командном режиме среды MATLAB:

После чего определяем нули функции:

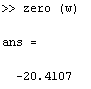
Все «нули» данной передаточной функции отрицательны, таким образом САУ в разомкнутом состоянии устойчива.

Д ля устойчивости замкнутой системы необходимо и достаточно, чтобы амплитудно-фазовая характеристика разомкнутой системы не охватывала точку (-1, 0)

>> nyquist(w)

Рисунок 9 - Годограф Найквиста

Годограф не охватывает точку (-1, j0). Следовательно система устойчива.

2.4 Исследование точности системы

2.4.1 Анализ влияния коэффициента усиления разомкнутой сау на устойчивость

Для определения границы устойчивости системы используем инструментом GUI-интерфейс SISO-Design Tool из пакета прикладных программ Control System Toolbox

>> w=tf([0.03263 0.666],[0.000000412 0.000049 0.000913 0.051 0])

Transfer function:

0.03263 s + 0.666

-----------------------------------------------------

4.12e-007 s^4 + 4.9e-005 s^3 + 0.000913 s^2 + 0.051 s

>> p=zpk('p'); w=(18*0.037*(0.049*p+1))/(0.357*(0.02*0.01*0.118*0.049*p^4+0.02*0.118*p^3*(0.049+0.01)+0.02*p^2*(0.118+0.01)+(0.118*(0.049+1)*p)))

Ноль/Полюс/Увеличение:

79048.5686 (p+20.41)

--------------------------------

p (p+109.1) (p^2 + 11.3p + 981)

На основе zpk объекта вызовем SISO-Design Tool командой Sisotool(w)

>> sisotool(w)

Рисунок 10 - Годограф Михайлова.

Передвигая красным курсором по годографу до пересечения с мнимой осью, и определим коэффициент усиления, при котором система находится на границе устойчивости:

Рисунок 11 - Пересечение с мнимой осью

В результате был найден коэффициент усиления, равный 0,72, при котором система находится на границе устойчивости.

Рисунок 12 - Значения полюсов

Рисунок 13 - Пересечение с мнимой осью

Рисунок 14 - Значения полюсов

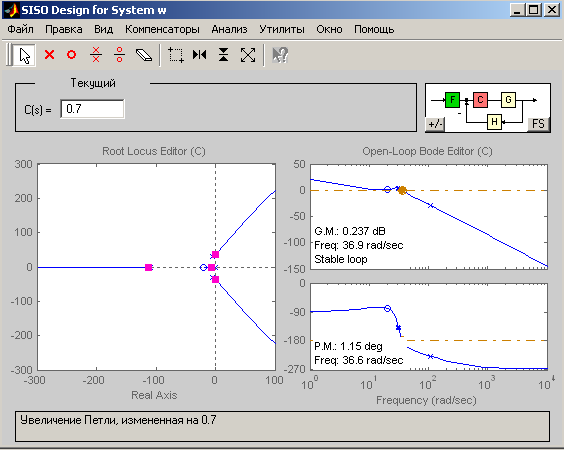
Рисунок 15 - Пересечение с мнимой осью

Рисунок 16 - Значения полюсов

На основе использования метода корневого годографа были получены области значений коэффициента усиления, в которых система автоматического управления является устойчивой.

2.4.2 Определение запасов устойчивости.

Изменение параметров (в частности увеличение коэффициентов усиления и запаздываний) в системах автоматического регулирования может вызвать неустойчивость. Поэтому при проектировании систем регулирования стремятся обеспечить их устойчивость с некоторой гарантией, так что бы изменение параметров в некоторых пределах не могло привести к неустойчивости. Для этой цели используются понятия запасов устойчивости систем. Различают запас устойчивости по амплитуде (модулю) и по фазе. Запасы устойчивости наиболее удобно определять используя логарифмические частотные характеристики.

Найти их можно c помощью команды bode(w)

>> bode(w)

Рисунок 17 - Диаграмма Боде

Для построения переходной характеристики воспользуемся командой step(w).Результат ее выполнения приведен на рисунке ниже.

>> step(w)

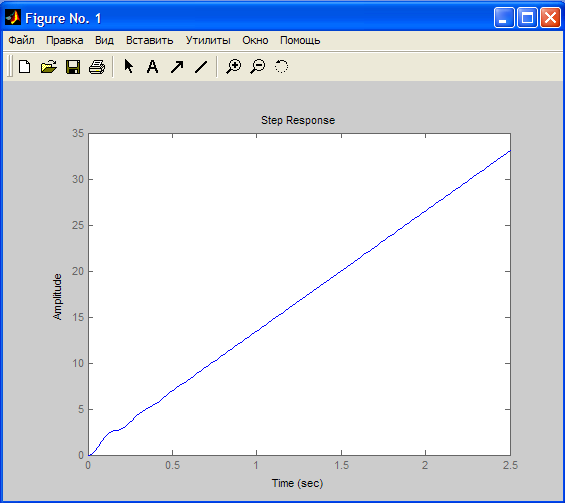
Рисунок 18 - Переходная характеристика.